深度强化学习】Gumbel-Softmax：离散随机变量的重参数化（reparameterization）

转自：https://zhuanlan.zhihu.com/p/551255387

以DDPG为代表的确定性策略梯度算法只适用于连续动作空间的任务，为了让这些算法能够处理离散动作空间的任务，需要对其进行Gumbel-Softmax处理，这篇笔记将从强化学习的角度出发，对为什么需要以及怎么使用Gumbel-Softmax进行简单介绍。

回顾一下在强化学习中有两类策略梯度的估计方法：

【随机策略梯度定理】根据Sutton提出的 随机策略梯度定理，如果∇𝜃𝜋𝜃(𝑎∣𝑠)


存在，那么 随机策略的策略梯度可以计算为

∇𝜃𝐽(𝜋𝜃)=∫𝑆𝜌𝜋(𝑠)∫𝐴∇𝜃𝜋𝜃(𝑎∣𝑠)𝑄𝜋(𝑠,𝑎)d𝑎 d𝑠=𝐸𝑠∼𝜌𝜋,𝑎∼𝜋𝜃[∇𝜃log⁡𝜋𝜃(𝑎∣𝑠)𝑄𝜋(𝑠,𝑎)]

【确定性策略梯度定理】根据David Silver提出的 确定性策略梯度定理，如果 ∇𝑎𝑄𝜇(𝑠,𝑎) 与 ∇𝜃𝜇𝜃(𝑠) 存在，那么确定性策略的策略梯度可以计算为

∇𝜃𝐽(𝜇𝜃)=∫𝑆𝜌𝜇(𝑠)∇𝜃𝜇𝜃(𝑠)∇𝑎𝑄𝜇(𝑠,𝑎)|𝑎=𝜇𝜃(𝑠)d𝑠=𝐸𝑠∼𝜌𝜇[∇𝜃𝜇𝜃(𝑠)∇𝑎𝑄𝜇(𝑠,𝑎)|𝑎=𝜇𝜃(𝑠)]=𝐸𝑠∼𝜌𝜇[∇𝜃𝑄𝜇(𝑠,𝑎)|𝑎=𝜇𝜃(𝑠)]

可以看出，确定性策略梯度与随机策略梯度的计算有很大的区别，随机策略梯度对应随机策略， 𝜋𝜃(𝑎|𝑠) 表示的是状态 𝑠 下智能体采取动作 𝑎 的概率，而确定性策略梯度对应的是确定性策略，𝜇𝜃(𝑠) 对应的即为智能体即将采取的动作 𝑎。

随机策略梯度定理存在的条件是 ∇𝜃𝜋𝜃(𝑎∣𝑠) 存在，也就是 𝜋𝜃(𝑎∣𝑠) 对 𝜃 可微，很显然，我们常见的，针对离散动作的类别（categorical）分布与针对连续动作的高斯分布，所对应的概率密度函数，都可以用神经网络进行参数化表示，对 𝜃 都是可微的，这也就是为什么基于随机策略梯度的算法（REINFORCE，PPO等）既能处理离散任务，也能处理离散任务。

确定性策略梯度定理存在的条件则是 ∇𝜃𝜇𝜃(𝑠) 存在，也就是动作 𝜇𝜃(𝑠) 本身对 𝜃 可微，对于连续动作的确定性策略，可以直接用一个参数为 𝜃 的神经网络拟合 𝜇𝜃(𝑠)，再添加一个随机噪声探索，此时 ∇𝜃𝜇𝜃(𝑠) 是存在的。但是对于离散动作，我们无法用神经网络直接输出一个可导的离散变量。在神经网络中，为了输出离散值，一个通常的做法是先输出每个动作的logits，然后通过一个softmax层将其转化为每个动作的概率。此时我们可以直接采用 argmax 操作输出概率最大的动作，但这种方法：1. 无法对动作空间进行探索；2. argmax操作是不可导的，无法回传梯度。为了解决第一个动作探索的问题，可以根据softmax输出的概率值对动作进行 采样，然而采样这个操作同样是不可导的，因此同样不可行。

在上面两段描述中，我个人觉得比较难以理解的点是为什么随机策略中采样可导，而确定性策略中采样不可导。这是因为随机策略中只要求概率密度函数对 𝜃 可导，这跟采样本身是没有关系的，而在确定性策略中，要求的是动作本身对 𝜃 可导，如果引入了随机策略采样，那么采样就是得到动作的最后一步操作，因此被纳入了求梯度的过程，而采样本身又不可导，这就是为什么最初的确定性策略梯度只能用于确定性策略。

既然采样操作不可行，那怎么保证确定性策略的探索呢？这就涉及到了重参数化（Reparameterization）这一重要技巧，首先从比较常规的连续动作下的reparameterization进行介绍。

确定性策略梯度中连续变量的重参数化（Reparameterization）

在确定性策略梯度框架下，我们要求策略：1. 能够保证探索；2. 可导。为了保证探索，有两种常见的方法，一种是直接使用随机策略，但这涉及到采样的操作，不可导；另一种是在确定性策略上添加噪声。实际上确定性策略添加噪声之后相当于也是随机策略，只不过此时采样过程和梯度的计算图分离了，这样就保证了梯度的可求，这种方法实际上就隐含了重参数化（reparameterization）的思想。为了更加清楚地解释reparameterization的含义，接下来先用SAC来介绍reparameterization。

XuanAxuan：【深度强化学习】最大熵 RL：从Soft Q-Learning到SAC121 赞同 · 40 评论文章

确定性策略梯度是针对确定性策略提出的，SAC沿用了DDPG的确定性策略思想，使用的却是随机策略，这实际上就是因为SAC用到了reparameterization的技巧。SAC中的随机策略 𝜋𝜃(𝑎|𝑠) 是一个均值为 𝜇𝜃𝜇 ，方差为 𝜎𝜃𝜎高斯分布，均值 𝜇𝜃𝜇 和方差 𝜎𝜃𝜎 均用神经网络表示，此时策略梯度的计算公式为（最大熵框架，详细推导见SAC）

∇𝜃𝐽(𝜋𝜃)=𝐸𝑠∼𝐷[𝐸𝑎∼𝜋𝜃[∇𝜃(𝛼log⁡(𝜋𝜃(𝑎|𝑠))−𝑄(𝑠,𝑎))]]

很显然，这里有一个 𝑎∼𝜋𝜃 的采样操作，是没有办法对 𝜃 进行求导的。为此，SAC的作者提出将 𝑎 这样一个复杂的随机变量用一个简单的随机变量来表示，即用 𝑓𝜃(𝜖,𝑠) 来表示 𝑎，这里 𝜖 是服从 𝜖∼𝑁(0,1) 的标准高斯随机变量。具体而言，𝑎=𝑓𝜃(𝜖,𝑠)=𝜇𝜃𝜇⋅𝜖+𝜎𝜃𝜎，显然，此时 𝑎 仍然服从最初设定的均值为 𝜇𝜃𝜇，方差为 𝜎𝜃𝜎 的高斯分布 𝜋𝜃(𝑎|𝑠)，也就是说，reparameterization不会改变随机变量原本的分布。这么做有什么用呢？让我们继续对梯度进行推导：

∇𝜃𝐽(𝜋𝜃)=𝐸𝑠∼𝐷[𝐸𝑎∼𝜋𝜃[∇𝜃(𝛼log⁡(𝜋𝜃(𝑎|𝑠))−𝑄(𝑠,𝑎))]]=𝐸𝑠∼𝐷[𝐸𝜖∼𝑁[∇𝜃(𝛼log⁡(𝜋𝜃(𝑓𝜃(𝜖,𝑠)|𝑠))−𝑄(𝑠,𝑓𝜃(𝜖,𝑠)))]]=𝐸𝑠∼𝐷[𝐸𝜖∼𝑁[∇𝜃𝛼log⁡(𝜋𝜃(𝑎|𝑠))+∇𝑎(𝛼log⁡(𝜋𝜃(𝑎|𝑠))−𝑄(𝑠,𝑎))∇𝜃𝑓𝜃(𝜖,𝑠)]]

可以看出，原本我们需要从未知分布 𝜋𝜃(𝑎|𝑠) 进行采样，采样过程与参数 𝜃 有关，不可导，而通过reparameterization，我们只需要从已有的分布 𝑁(0,1) 进行采样， 采样的过程不再与 𝜃 有关，因此不会被包含进梯度的计算中，此时我们就可以直接根据链式法则对梯度进行计算了！！简单来说，reparameterization实际上就是将随机性采样和计算图的构建剥离开来，从而避免了采样过程对梯度计算的干扰。

实际上，DDPG本身也采用了reparameterization，此时 𝑎=𝑓𝜃(𝜖,𝑠)=𝜇𝜃+𝜖⋅𝜎，因此 𝑎 服从均值为 𝜇𝜃，方差为 𝜎 的高斯分布，这里 𝜎 是超参数。因此，SAC和DDPG的思想没有本质区别，只不过是SAC引入了最大熵框架，能够自动调节动作的方差，探索能力更强，超参数更少，因而比DDPG稍微高级一点。

Gumbel-Softmax：离散变量的重参数化（Reparameterization）

上面介绍了针对连续高斯分布的reparameterization，那么针对离散变量的categorical分布要怎样进行reparameterization呢？从上面SAC和DDPG的例子可以看出，reparameterization有两个要求：1. 不改变原有概率分布；2. 可导。Gumbel-Softmax正符合了这两个要求。

在离散任务中，𝑎 是一个离散的随机变量，它对应 𝑘 个不同的动作，依据当前策略，每个动作的概率为 𝜋𝜃1，𝜋𝜃2，...,𝜋𝜃𝑘，所有动作的概率加起来为1。如果直接取概率最大值的动作或依据这些概率对动作进行采样，则均不可导。为此，我们首先引入一个服从Gumbel(0,1)分布的随机变量。

【Gumbel(0,1)分布】𝑔=−log⁡(−log⁡(𝜖))，其中 𝜖∼𝑈(0,1)，𝑔 即服从Gumbel(0,1)分布。

根据原来的概率分布和Gumbel噪声可以构造一个Gumbel-Max随机变量：

【Gumbel-Max】𝑎=arg⁡max𝑖(log⁡(𝜋𝜃𝑖)+𝑔𝑖)。

可以看出，Gumbel-Max实际上就是一个reparameterization的过程，首先根据已有的Gumbe(0,1)分布采样得到噪声 𝑔𝑖，然后再结合随机策略得到的概率构造出Gumbe-Max随机变量，这样就将采样的过程从梯度的计算中分离开来了。

我们首先可以证明Gumbe-Max所得到得的随机变量服从原来的依据概率 𝜋𝜃1，𝜋𝜃2，...,𝜋𝜃𝑘 的分布（参考漫谈重参数：从正态分布到Gumbel Softmax - 科学空间|Scientific Spaces (kexue.fm)），因此满足了reparameterization的第一个条件。

然而，此时还是有一个 arg⁡max 操作，因此还是不可导的。为此我们需要得到一个 arg⁡max 的可导近似，实际上就是 softmax。在神经网络中，我们通常把离散变量写成one hot形式，例如3个离散动作表示成001,010,100。arg⁡max 最终得到的实际上也是一个one hot（最大概率动作对应的onehot），而gumbel-softmax得到的就是one hot变量的一个连续近似。

【Gumbel-Softmax】softmax(log⁡(𝜋𝜃𝑖)+𝑔𝑖)，即

exp⁡((log⁡(𝜋𝜃𝑖)+𝑔𝑖)/𝜏)∑𝑗=1𝑘exp⁡((log⁡(𝜋𝜃𝑗)+𝑔𝑗)/𝜏) for 𝑖=1,…,𝑘

Gumbel-Softmax为每个离散动作得到了一个新的概率，举例来说，根据gumbel-softmax计算得到（0.997,0.001,0.002），此时这个值就对应着onehot向量100的近似。𝜏 是一个温度系数，𝜏 越小，输出结果就越接近one hot形式。

通过这样一个Gumbel-Softmax的操作，得到最终动作 𝑎 的过程就可导了。那么问题来了，此时所得到的gunbel-softmax变量虽然可导，但是是一个连续值，并非真正的one-hot变量。因此，在实际的操作中，我们在前传时，直接使用Gumbel-Max输出动作，但在梯度回传过程中，则采用Gumbel-Softmax来估计梯度。在代码中体现为：

# 利用.detach() 将gumbel-max操作从计算图分离开，再在计算图上增加gumbel-softmax操作，但实际的结果还是gumbel-max
a = (a_gumbel_max - a_gumbel_softmax).detach() + a_gumbel_softmax

总结来说，通过Gumbel-Max，对采样过程进行了reparameterization，将采样从梯度的计算中剥离开来，然后通过在梯度过程用Gumbel-Softmax替代Gumbel-Max，进一步保证了梯度的可计算性。

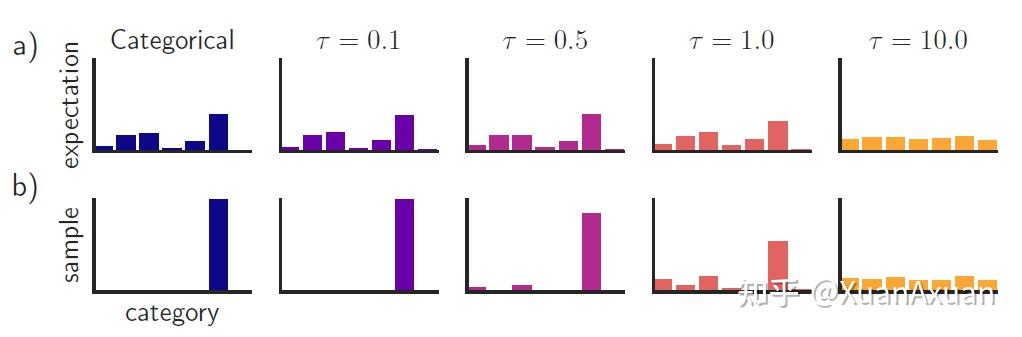
下面这幅图将原Categorical分布与Gumbel-Softmax分布进行了对比（只有第一列是Categorical分布），可以看出，当 𝜏 很小时，Gumbel-Softmax与原分布十分接近，采样得到的结果也与原分布相同，当 𝜏 比较大时，各个动作的概率就会趋近于相等。在实验中，需要对 𝜏 进行合理地选取。

MADDPG中的Gumbel-Softmax

根据FACMAC算法提供的代码，在MADDPG-discrete算法中，action的选择分为四种情况：

• 训练过程中的采样阶段：该阶段的作用主要是对各种不同动作进行探索，无需用到Gumbel-Softmax，此时动作的选择分为四步：
• step1：神经网络输出每个离散动作的logits
• step2：对logits进行softmax处理，得到每个动作的采样概率 𝜋𝑖
• step3：将采样概率 𝜋1,𝜋2,... 与对应均匀分布的采样概率加权求和，得到探索时的采样概率
• step4：依据上面求得的概率对动作采样
• 训练过程中的critic网络更新阶段：该阶段的作用是对critic网络进行更新，根据DDPG的critic更新公式，此时只需要利用target actor网络输出logits，然后根据该logits构造one-hot动作向量即可，也无需用到Gumbel-Softmax
• 训练过程中的actor网络更新阶段：该阶段的作用是对actor网络进行更新，需要对动作进行求导，因此需要用到Gumbel-Softmax，此时动作的选择分为四步：
• step1：神经网络输出每个离散动作的logits
• step2：计算得到logits对应的Gumbel-Softmax值
• step3：计算得到logits对应的Gumbel-Max值
• step4：利用a = (a_gumbel_max - a_gumbel_softmax).detach() + a_gumbel_softmax 输出one-hot向量，但保留Gumbel-Softmax的梯度
• 测试阶段：该阶段直接利用actor网络输出logits，然后根据该logits构造one-hot动作向量

在这种情况下，采集样本过程中对动作的采样过程和actor网络更新过程中的动作采样过程是不一样的。而在epymarl提供的代码中，探索阶段也是直接使用Gumbel-Softmax进行探索。我也不清楚哪种方法更加科学。

总结

其实Gumbel-Softmax是个蛮简单的操作，但背后的原理我一直没太搞明白，于是仔细学了一下，发现这和SAC里的reparameterization不是很相似吗？当时写SAC笔记的时候其实对reparameterization没太搞明白，昨天把这两个东西放在一起，发现就很好理解了，只不过一个是连续的，一个是离散的。理解了之后就想写下来，写完了发现有些地方还是很难表述清楚，大家凑合着看吧！！如果有不准确的地方欢迎在评论区指出来hhh