Conservative Q Learning(保守强化学习)傻瓜级讲解和落地教程

转自：https://zhuanlan.zhihu.com/p/603691759

一句话概括CQL：通过打压OOD(out of distribution)的q值的同时，去适当的鼓励已经在buffer(训练集)中的q值，从而防止q值被高估。论文中严格证明了通过该方法，能确保学习到q值的下界值，避免了被高估。

我们从最最初的版本出发，一路到后面，确保有强化学习基础的所有人读一遍就能懂。

 

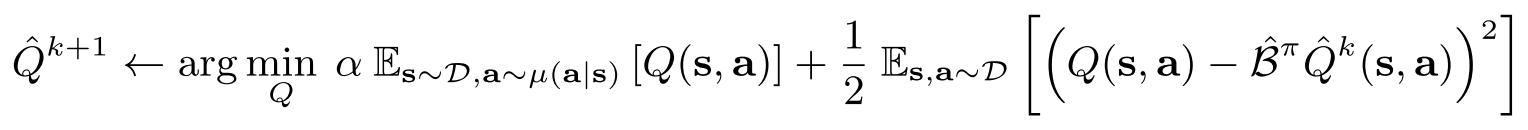
上图是一个更新q值的公式，包括两项。加号右边的那一项就是我们通过MSE去更新q值，这个不需要在原代码上去做什么修改。 β是bellman算子，但是好像代码里这部分基本都不会考虑，直接设置为1就行。

主要看的是左边的Q(s, a)。注意，这里的state来自replay buffer，action为当前的actor在这个state的下所选择的action。这部分的Q值我们会进行minimize，也就是“打”。为什么要打压这个值呢，因为这个action是当前policy作出的action，其实这个action很可能并没有在真实的环境中出现过，所以可能对这个Q(s,a)我们的估值是没有那么的，所以我们要对这个点进行一定程度的打压。这里的μ就可以理解为你要训练的那个actor。

 接下来是鼓励的部分。

 

 红色部分是我们要最大化的点(最小化负值=最大化原值)。这部分的state来自replay buffer，同时action也来自replay buffer。也就是说这个pair对是通过策略和真实环境中交互中得到的，这部分已经出现在训练集中的pair对，我们其实是可以认为预估可能相对比较准确，不太需要打压了，所以理应得到一些鼓励。

 在论文中，除了这两部分，还加入了一个正则化项。

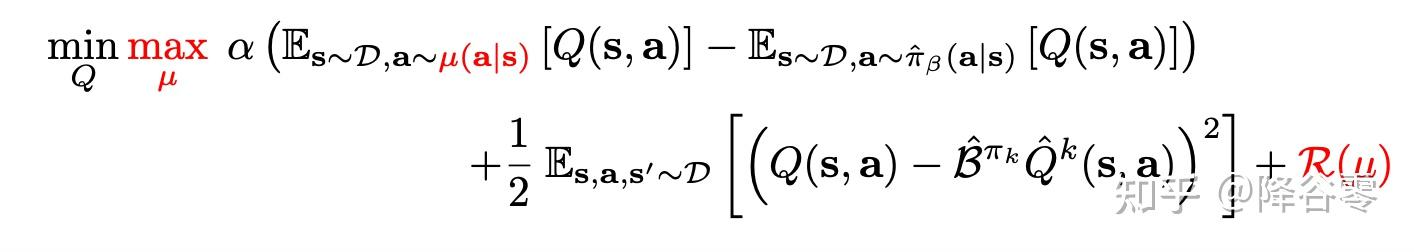
  这部分正则化项是一个KL散度，防止过拟合，可以理解为当前策略和某一个先验策略的KL散度，通常会取均匀分布。

但是文章贴心的帮我们进行了简化，我们最终要落地的目标函数如下：

 

KL的部分和打压的部分被融为一体了，推导不是很难，可以参考论文，接下来介绍落地环节。

接下来看代码部分讲解，相信大家都有一些tensorflow和pytorch的基础

在实际的落地中，我们根据论文附录部分的讲解进行落地

论文中将损失函数log的部分拆解为了图中的形式，详细介绍一下如何实现这个。其实就是进行采样，采样那些需要打压的点。

采样过程分为三个环节：

首先，在均匀分布中采样N个点，这个实现起来非常简单

# num_random表示采样的次数
# random_unif_log_pi表示得到均匀分布的log_prob
random_unif_actions = torch.rand(
            [batch_size * self.num_random, actions.shape[-1]],
            dtype=torch.float).uniform_(-1, 1).to(device)
random_unif_log_pi = np.log(0.5**next_actions.shape[-1])

其次，在当前state的分布中，采样N个点

此处的states来自于训练集(buffer)中，将该state输入到actor中，如果是连续的动作值，通过高斯分布采样得到random_curr_actions, 以及可以得到对应的log_pi。降谷零：PPO2复现详细流程(更新github代码)介绍过如何得到log_prob，不管是pytorch还是tensorflow都很方便。

tmp_states = states.unsqueeze(1).repeat(1, self.num_random,
                                                1).view(-1, states.shape[-1])
random_curr_actions, random_curr_log_pi = self.actor(tmp_states)

再次，在下一个state的分布中，采样N个点。

同样，此处的next_states中也来自于训练集中，其他的和上面一样

tmp_next_states = next_states.unsqueeze(1).repeat(
            1, self.num_random, 1).view(-1, next_states.shape[-1])
random_next_actions, random_next_log_pi = self.actor(tmp_next_states)

现在我们就到了采样的action以及对应的log_prob，分别来自于均匀分布、当前s的高斯分布以及下一个s的高斯分布。我们下一步需要得到Q(s,a)，也就是需要打压的q。这很简单，把得到的(s,a) pair对输入到critic中就行了，得到q1_unif, q1_curr, q1_next。

接下来就是比较关键的步骤了。

q1_cat = torch.cat([
            q1_unif - random_unif_log_pi,
            q1_curr - random_curr_log_pi.detach().view(-1, self.num_random, 1),
            q1_next - random_next_log_pi.detach().view(-1, self.num_random, 1)
        ],
#or no importance sampling
q1_cat = torch.cat([
            q1_unif,
            q1_curr,
            q1_next
        ],

这里对应的部分就是

 

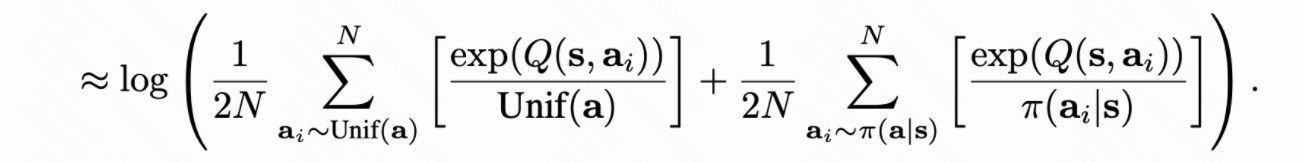
这部分是将期望的符号去除，变成累加。论文中说到，如果是discrete的，直接除以采样的个数计算均值来代表期望；如果是连续的动作，通过importance sampling来计算这个数量，计算期望。但实际落地应该也可以忽略掉这部分，也是就是直接把q值进行连接，不需要考虑importance sampling。

下一步就是计算logexpsum了。示例代码用的是SAC，所以有两个Critic。

qf1_loss_1 = torch.logsumexp(q1_cat, dim=1).mean()
qf2_loss_1 = torch.logsumexp(q2_cat, dim=1).mean()

#这两行代码计算的是buffer内部的states，action的q值。直接从buffer中读取state和action就行

qf1_loss_2 = self.critic_1(states, actions).mean()
qf2_loss_2 = self.critic_2(states, actions).mean()

#下面就是最终的loss了，正常的critic_loss+cql部分。

qf1_loss = critic_1_loss + self.beta * (qf1_loss_1 - qf1_loss_2)
qf2_loss = critic_2_loss + self.beta * (qf2_loss_1 - qf2_loss_2)

CQL部分讲解完成。