数据结构【树状数组】
树状数组是线段树的衍生产物，牺牲了部分通用性，节约了空间，且大大减少了手写码量， 借助树状数组，我们可以用O(logN)的时间复杂度来实现给定序列中长度为n的区间中元素和的计算。
https://www.bilibili.com/video/BV1ce411u7qP/?spm_id_from=333.337.search-card.all.click&vd_source=5795184162077d9b7f04406dc36caa90
这个视频讲解树状数组讲解得很形象，但不透彻，透彻的说法见下文。
从视频给出的可视化描述中，我们发现，对于一个长度为n的原序列而言，我们需要n/2个内含长度为1的树状数组元素（简称树元），还需要n/2/2个个长度为2的树元，以此类推，我们最终恰好需要n个树元构成的序列来存储原序列所含信息，其中每个树元所代表的区间的右端点都不同。
对于每一个树元，我们需要存储三个信息：所内含元素个数、所内含最后一个元素的下标、所内含元素的和。 但是，我们既然已经发现，我们需要存储的区间恰好有n个，并且这n个区间的右端点恰好不同，也就是说，唯一的右端点唯一对应着一个区间，而唯一的区间显然又唯一对应着一个区间长度。
那么我们就可以建立一个右端点->区间长度的映射函数，恰好，lowbit(x)=x~(-x)这个单参数函数可以完成这个任务（暂时别管为什么能，动手证明一下就会发现确实能，证明很简单）。这也就意味着，所内含元素个数和所内含最后一个元素的下标其实是同一个信息，只要存储了后者，就可以用lowbit函数算出前者。
至于lowbit为何能如此呢？这是因为我们把线段树转化为树状数组之后，所有树元的区间长度和右端点的关系都恰好和lowbit这个纯算术运算过程完全重合了，因此直接把这个函数拿过来用，至于这个伟大的巧合是谁发现的？想必是个大牛。但其实这倒也不完全是拉马努金式的发明，毕竟lowbit函数其实也可以通过数学手段直接从树状数组取区间的规则中直接反向推算出来，具体过程中文互联网上可能查不到，但无关主线且并不高深，我这里就不多赘述了
因此，我们对于每一个树元，只需要存储两个信息：所内含最后一个元素的下标、所内含元素的和，即右端点序号和树元值。 注意到，右端点序号恰好是1~n，那么我们直接把对应右端点序号的树元值存入对应下标的数组空位中，我们就可以实现用下标本身来存储右端点序号，而用数组本身的存储空间来存储树元值。 这样的一个数组，便是树状数组了。对于树状数组T而言，T[i]是右端点为i，区间长度为lowbit(i)的原序列区间的和。
仅仅如此还不够，我们还可以lowbit中挖掘出更多性质，比如，如果我们要求前i项的和，我们只要求出递归地减去lowbit(i)的过程中遇到的树元值的和，便得到了答案。再比如对于下标为i的树元而言，递归的加上lowbit(i)所得的所有树元恰好是包含他区间的所有树元，这很显然，因为lowbit(i)就是区间长度，加上下标区间长度之后对应的新区间可不就是原区间的母区间吗，借助这个性质可以实现对元素的修改，这两个比如说起来比较抽象，但是看看下图，再看看代码，就很容易能够理解了，再不懂就回头看看视频。
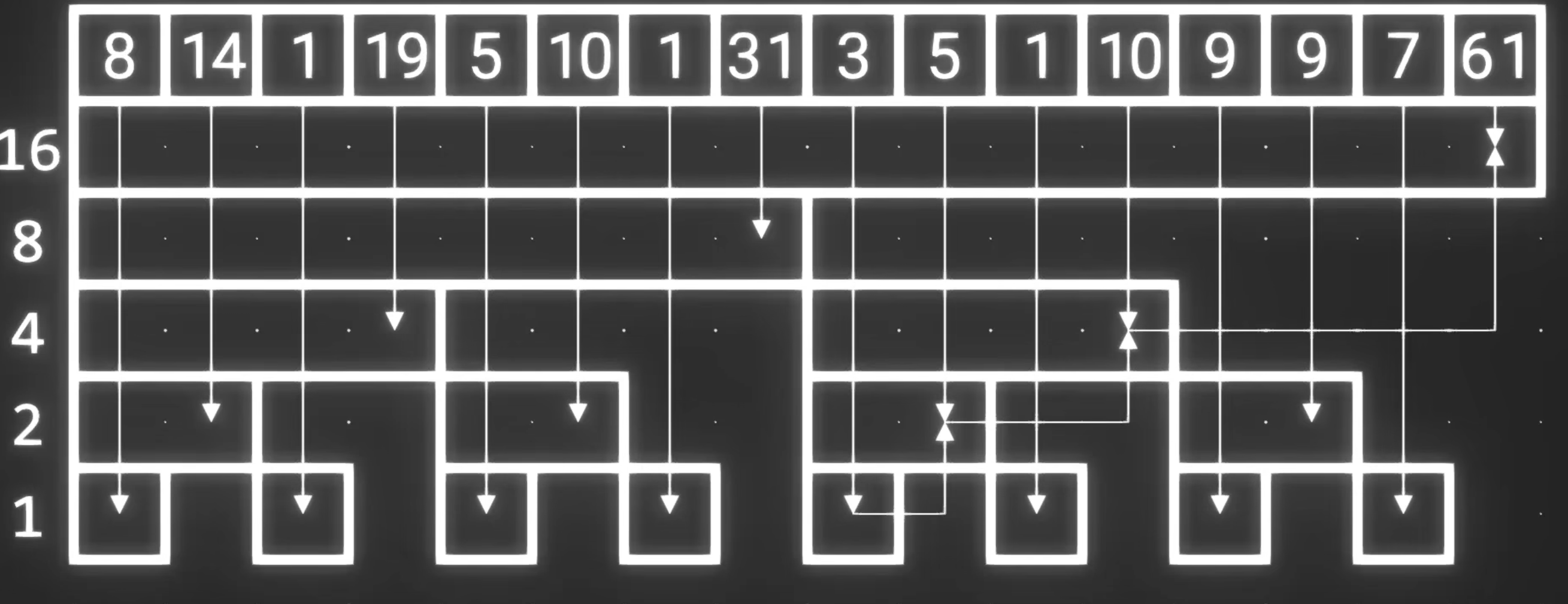
这个过程不难写成代码,如下
1 int T[200000+5];//树状数组 2 inline int lowbit(int x){return x&-x;} 3 inline int query(int x)//取前n项和 4 { 5 int res=0; 6 for(;x>=1;x-=lowbit(x))res+=T[x]; 7 return res; 8 } 9 inline void add(int x,int k) 10 { 11 for(;x<=n;x+=lowbit(x))T[x]+=k; 12 }
代码本身很简单，关键在于能否理解代码背后的过程，上文描述的就是我归纳出的科学家一步步发明线段树组的过程，理解了这个过程便理解了代码背后的思想
