主成分分析法笔记【零基础数模系列】
前言
作为数模小白，看了很多讲解新概念新模型的文章，这些文章往往要么讲的很浅不讲原理只讲应用，让人知其然不知其所以然。要么讲的很深小白看不懂，同时总是忽略关键部分，经常性引入陌生概念让初学者疑惑，因此有了本文，任何能熟练掌握线性代数知识且逻辑思维能力尚可的人都可以理解，而无需其他数模知识，涉及任何新概念都会先讲解后使用
所以我就打算把自己学完之后的笔记整理出来，其中每一篇文章中可能含有直接从其他文章中搜集过来的公式，因为这些文章原本只是我自己的笔记，我懒得敲公式，只是写完之后想着整理出来，弘扬一下互联网精神，于是就有了这个系列。
主成分分析（PCA）
主成分分析其实就是数据降维，基本思想是设法将原来众多的具有一定相关性的多个指标，重新组合成一组新的、较少的、互不相关的综合指标。从而在损失信息量较小情形下，将指标量大大缩减。
PCA的步骤如下：
1.标准化（白化），即数据预处理
标准化首先应该消除量纲的影响，让用m表示的数据和用cm表示的数据能显示出同样的方差，通常利用公式
来进行数据标准化。
标准化后不同指标的数据期望都是0，方差均为1，方面进行不同指标之间的运算，也消除了单位大小导致的不同方差。
2.计算相关矩阵R（这一步其实就是协方差分析）
首先，新引入一个概念——协方差矩阵，对于矩阵A而言，协方差矩阵为A’A，则显然协方差矩阵是实对称矩阵，那么协方差矩阵的特征值满足
进而有
我们取单位特征向量则有(Ax)’(Ax)=Lambda,而Ax的模长是每个向量在x方向的投影值，则Lambda=(Ax)’(Ax)就是所有点在x上投影的平方和，最大特征值对应的特征向量的方向就是投影平方和最大的方向。
因此协方差矩阵相似对角化所用的正交相似因子Q描述了一个新的坐标系，这个坐标系的每个由A’A特征向量指明的方向上矩阵A所描述的点集的投影的平方和就是与该向量对应的特征值。
而主成分分析其实就是经过一个用协方差矩阵的正交变换因子做正交变换后把旧指标转换为相互正交的新指标（即新坐标轴）的过程，每个新指标就是一个主成分，而所谓的投影平方和，其实就是原始数据点（每个数据点代表了一个“结构体”，一个“状态向量”）在这个坐标轴方向的方差，这个值越大说明原始数据在新指标下对应的数值的方差越大，说明这各新指标是个重要的新指标。因此协方差矩阵较大特征值对应的特征向量（即主成分）就是更重要的主成分，因此我们用
来衡量主成分的重要性并取足够多的几个主成分，若方差贡献率最大的m个主成分的累计贡献率达到足够大的阈值（一般取85%为阈值），那么这m个主成分就可以用来代表原本p个指标，m个主成分的列向量蕴含了大部分原本p个指标列向量综合的信息。然后用线性变换Q（以谁为新基向量组则右乘谁，方向没饭）使得X转化为F=XQ，F中就是在新坐标各数据的坐标。（这很合理，被淘汰的新坐标都是方差较小的，即各大结构体的这一指标都基本相等，那自然没必要关注，同时每个新指标都是由原本多指标变换过来的，他为常数其实暗示了原本指标之间满足某个线性方程，淘汰掉他其实就是淘汰掉了冗余指标之间的相关性）
设X为标准化后的数据矩阵，则X相关矩阵R。若X是n*p的矩阵，则矩阵R是p*p的矩阵，
（i,j∈[1，p]), rij表示X矩阵中第i列和第j列的相关关系，其值在-1到1之间，显然rij=rji，rij绝对值越接近于1则指标i与指标j的线性相关性越强，rij=1时两指标完全正线性相关 ，rij=-1时两指标完全负线性相关。
一般而言我们有
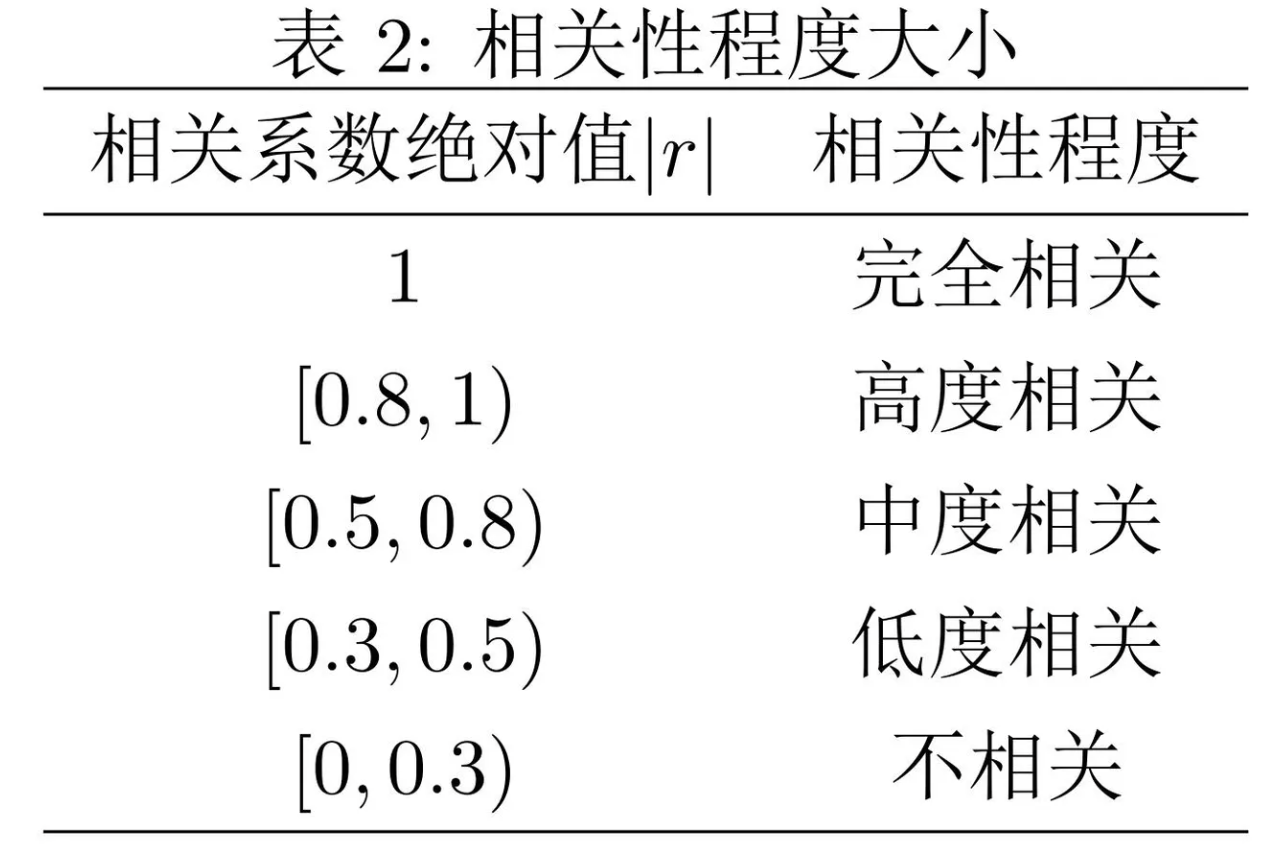
则根据协方差矩阵的性质我们发现相关矩阵R其实就是X的协方差矩阵，设使R相似对角化的正交变换因子为Q，则F=X·Q所描述的点就是在主成分坐标系中各结构体的新坐标。
最后按照贡献率权重加权可以算出各个结构体新坐标的综合得分从而实现排序
然而，新坐标本身就是加过权的了，方差大的坐标显然是由更多且系数更大的原坐标转换过来的，再加一次权并不是很科学，文章https://www.doc88.com/p-0761466936925.html就指出了这一问题，因此不如直接简单加和算总得分，简单加和法反而更科学。当然这一说法本身仍有争议，因此两份代码均给出，前面的是加权法，后面的是简单加和法，我更认可后者。
代码就很简单喽
简单加和法：
A = [
1.0000 40.4000 24.7000 7.2000 6.1000 8.3000 8.7000 2.4420 20.0000;
2.0000 25.0000 12.7000 11.2000 11.0000 12.9000 20.2000 3.5420 9.1000;
3.0000 13.2000 3.3000 3.9000 4.3000 4.4000 5.5000 0.5780 3.6000;
4.0000 22.3000 6.7000 5.6000 3.7000 6.0000 7.4000 0.1760 7.3000;
5.0000 34.3000 11.8000 7.1000 7.1000 8.0000 8.9000 1.7260 27.5000;
6.0000 35.6000 12.5000 16.4000 16.7000 22.8000 29.3000 3.0170 26.6000;
7.0000 22.0000 7.8000 9.9000 10.2000 12.6000 17.6000 0.8470 10.6000;
8.0000 48.4000 13.4000 10.9000 9.9000 10.9000 13.9000 1.7720 17.8000;
9.0000 40.6000 19.1000 19.8000 19.0000 29.7000 39.6000 2.4490 35.8000;
10.0000 24.8000 8.0000 9.8000 8.9000 11.9000 16.2000 0.7890 13.7000;
11.0000 12.5000 9.7000 4.2000 4.2000 4.6000 6.5000 0.8740 3.9000;
12.0000 1.8000 0.6000 0.7000 0.7000 0.8000 1.1000 0.0560 1.0000;
13.0000 32.3000 13.9000 9.4000 8.3000 9.8000 13.3000 2.1260 17.1000;
14.0000 38.5000 9.1000 11.3000 9.5000 12.2000 16.4000 1.3270 11.6000;
15.0000 26.2000 10.1000 5.6000 15.6000 7.7000 30.1000 0.1260 25.9000]
a=size(A,1);%获得矩阵A的行大小
b=size(A,2);%获得矩阵A的列大小
for i=1:b
SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i));%std函数是用来求向量的标准差
end
%计算相关系数矩阵的特征值和特征向量
CM=SA'*SA;%计算相关系数矩阵
[V,D]=eig(CM);%计算特征值和特征向量
for j=1:b
DS(j,1)=D(b+1-j,b+1-j);%对特征值按降序排列
end
for i=1:b
DS(i,2)=DS(i,1)/sum(DS(:,1));%贡献率
DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));%累计贡献率
end
% % 选择主成分及对应的特征向量
T=0.9;%主成分信息保留率
for k=1:b
if DS(k,3)>=T
Com_num=k;
break;
end
end
%提取主成分对应的特征向量
for j=1:Com_num
PV(:,j)=V(:,b+1-j);
end
% % 计算各评价对象的主成分得分
new_score=SA*PV;
for i=1:a
total_score(i,1)=sum(new_score(i,:));
total_score(i,2)=i;
end
result_report=[new_score,total_score];%将各主成分得分与总分放在同一个矩阵中
result_report=sortrows(result_report,-4);%按总分降序排序
% % 输出模型及结果报告
disp('特征值及其贡献率，累加贡献率：')
DS
disp('信息保留率T对应的主成分数与特征向量：')
Com_num
PV
disp('主成分得分及排序（按倒数第二列的总分进行排序，倒数第一列是企业编号，其余列是各主成分得分）')
result_report
浙公网安备 33010602011771号