清北学堂2019.8.7

Day 2 赵和旭

今天以背包DP，数位DP，树形DP和基环树为主（好多啊）

背包问题

0/1背包问题

给出n个物品，每个物品有Vi的价值和Wi的费用，我们总共有m块钱，求最多能得到多少价值的物品。

N<=10^3,m<=10^3

memset(dp,-0x3f,sizeof(dp));
dp[0][0]=0;
for (int i=1;i<=n;i++)
{
    for (int j=0;j<w[i];j++)
        dp[i][j]=dp[i-1][j];
    for (int j=w[i];j<=m;j++)
        dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
} 

更简便更省空间更常用的写法

memset(f,-0x3f,sizeof(f));
f[0]=0;
for (int i=1;i<=n;i++)
    for(int j=m;j>=w[i];j--)
        f[j]=max(f[j],f[j-w[i]]+v[i]);

设dp[i][j]表示前i个物品，用了j的体积得到的最大的价值。

则dp[i][j]=max{dp[i-1][j] , dp[i-1][j-w[i]]+v[i]}

若求方案数:

　　dp[i][j]=dp[i-1][j]+dp[i-1][j-w[i]]

完全背包

每一个物品可以选无限个。

dp[i][j]=max{dp[i][j-w[i]],dp[i-1][j]}

memset(dp,-0x3f,sizeof(dp));
dp[0][0]=0;
for (int i=1;i<=n;i++)
{
    for (int j=0;j<w[i];j++)
        dp[i][j]=dp[i-1][j];
    for (int j=w[i];j<=m;j++)
        dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i]);
} 

更简便更省空间更常用的写法

memset(f,-0x3f,sizeof(f));
f[0]=0;
for (int i=1;i<=n;i++)
    for (int j=w[i];j<=m;j++)
        f[j]=max(f[j],f[j-w[i]]+v[i]);

多重背包

对每一个物品，最多能用t[i]次。

memset(dp,-0x3f,sizeof(dp));
dp[0][0]=0;
for (int i=1;i<=n;i++)
    for(int j=0;j<=m;j++)
    {
        dp[i][j]=dp[i-1][j];
        for (int k=1;k<=c[i]&&k*w[i]<=j;k++)
            dp[i][j]=max(dp[i][j],dp[i-1][j-w[i]]+k*v[i]);
    }

 另一种写法同样简单一些

memset(f,-0x3f,sizeof(f));
f[0]=0;
for (int i=1;i<=n;i++)
    for (int j=m;j>=0;j--)
        for (int k=1;k<=c[i]&&k*w[i]<=j;k++)
            f[j]=max(f[j],f[j-k*w[i]]+k*v[i]);

多重背包可以进行优化：

优化一：

　　可以把t[i]拆成1+2+4+8…2^k+x, 这样k+1组，x小于2^(k+1) ，然后我们会发现这 些组能拼成0…　　t[i]每一种情况，然后这样我们就成了n*log(t[i])个物品的0/1背包 问题。

　　对于[0,2^(k+1)-1]都能拼成，所以[x,2^(k+1)-1+x]也都能拼成，x<=2^(k+1)-1，则 [0,2^(k+1)-1+x]　　全能拼成。

　　复杂度O(n*log(t[i])*m)

优化二：

　　我们来观察一下式子

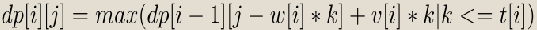
　　我们发现对于第二维，我们的j和能转移过来的j-w[i]*k在模w[i]意义下是同余的， 也就是说我们　　可以对于第二维按照模w[i]进行分类，不同类之间不会互相影响。

　　设f[j]=dp[i-1][j*w[i]+r]。r是我们枚举模w[i]的一个类。

 

实际上就是一个滑动窗口取最值的问题，直接单调队列优化即可。

老师的神奇板书。。。（传说中最为工整的）

分组背包

一共有n组，每组有size[i]个物品，第i组第j个物品的费用为w[i][j]，价值v[i][j]，每个组里的物品是互斥的，意味着你在一组物品中只能选择一个物品，求花费小于等于m能得到的最大价值。

Size之和小于等于1000，m<=1000

其实都是一样的。

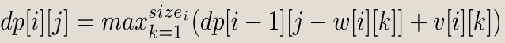
memset(f,-0x3f,sizeof(f));
f[0]=0;
for (int i=1;i<=n;i++)
    for (int j=m;j>=0;j--)
        for (int k=1;k<=size[i];k++)
            f[j]=max(f[j],f[j-w[i]]+v[i][k]);

经典例题

给出n个化学反应，每个反应消耗a[i]升氧气和b[i]升氢气，可以得到w[i]的价值，现在总共有X升氧气和Y升氢气，求我们最多可以得到多少价值。

n,a[i],b[i],X,Y<=100

此外还有二维背包问题，实质上和本身和普通背包毫无思维上的区别。

因为限制条件多了一个，所以我们需要给最初最基本的dp多加一维状态。

设dp[i][x][y]表示前i个物品，消耗了x的氧气和y的氢气所能得到的最大收益是多少。

然后考虑一个物品选还是不选即可。

vijos1240

1.给你一些房间，告诉你这些房间的容纳人数和价格。

2.安排一定数量的人住到旅馆里，满足：

a.不同性别的人如果不是夫妻那么不能住一个房间。

b.一对夫妻如果住在一起，那么房间不能安排其他的人进去哪怕房间没盛满人。

你来写一个程序帮助佳佳找到安排这些来参加旅行的人住进旅馆所需要的最小花费。

M：参加旅行的男性人数、 f：参加旅行的女性人数、 r：旅馆的房间数、c：这些男女中有多少对夫妻、Bi：每个房子容纳人数和、Pi：每个房子价格。注意每一个人不是单身就是和他/她唯一的妻子/丈夫一起参加旅行。

0<=m,f,r<=300，0<=c<=Min(m,f)，0<=Pi<=10。2<=Bi<=300

还是要先明确，对于一道背包dp的题目来说，我们需要有容量，物品，费用，价值（权值，因为有些题要求最小）。

本题中：求给所有的人安排房间的最小支出是多少？那么在这里，几个人对应就是dp的数组下标，每个房间就是一个物品，房间支出就是物品的权值。 虽然这里看上去房间支出是花费，是作为数组下标的存在，实际上是作为我们要求的东西，是dp数组存的内容。

首先要观察出题目的一个小性质，即如果有两对(或以上)夫妻住在一起的话，那么交换之后结果不会变差。因为首先这两个房间的容量至少为2，如果男男在一个房间，女女在一个房间此时花费不变，有一个房间容量大于2的时候，就还可以再入住其他人。这样结果变得更优了。 综上，要么至多存在1对夫妻住在一起，要么不存在夫妻住在一起。f[i,j,k,0]表示前i个房间住j名男性k名女性并且没有夫妇住在一起的最小花费f[i,j,k,1]表示前i个房间住j名男性k名女性并且有一对夫妇住在一起的最小花费

f[i,j,k,0]=min(f[i-1,j,k,0],f[i-1,j-v[i],k,0]+p[i],f[i-1,j,k-v[i],0]+p[i])

f[i,j,k,1]=min(f[i-1,j,k,1],f[i-1,j-v[i],k,1]+p[i],f[i-1,j,k-v[i],1]+p[i],f[i-1,j-1,k-1,0]+p[i])

Bzoj 1190

给你N颗宝石，每颗宝石都有重量和价值V。要你从这些宝石中选取一些宝石，保证总重量不超过W，且总价值最大为，并输出最大的总价值，每颗宝石的重量符合a*2^b。

V<=1e9，a<=10; b<=30

f[i][j]表示到第i位，剩下j*2^i的重量可用

看到w很大，看似不可做。

但是这题肯定能做啊！我们就找有什么特殊的约束条件。

w=a*2^b，我们发现a，b都不大，就启发我们用2^b分组。

将物品按b值从大到小排序分阶段处理，在阶段内b值都相同，直接忽略不足2^b的部分，f[i][j]表示前i个物品，剩余的能用重量为j*2^b的最大价值。

从上一阶段到下一阶段时，将f[i][j]->f ’[i][j*2+零碎部分]，注意到n=100，a<=10，所以剩余重量最多纪录到1000即可。

复杂度O（n*1000）

Bzoj3163 heoi2013 新背包问题

N个物品，第i个物品有c[i]个，购买第i个物品需要a[i]元，可获利b[i]的价值。有m个询问，每次询问：如果第x个物品禁止购买，你有y元的话，能获得的最大价值是多少？询问之间互相独立。

N<=1000,m<=3*10^5

分治+背包

初始solve(1,n)

递归的函数到Solve(l,r)，维护的dp数组，记录的是除去[l,r]外的物品的构成的背包数组。

Solve(l,mid)时，把[mid+1,r]内的物品加入dp数组。

我们这里定义的加入这个物品u，就是多考虑上这个物品之后构成的dp数组。

若是0/1背包的加入也就是做以下这个操作。

For (int i=n;i>=w[u];i--) dp[i]=max(dp[i],dp[i-w[u]]+v[u]);

当l=r时，将对应所有的询问在dp数组查询即可。

单调队列优化的话，复杂度O(n*m*log(n)),每个物品被加进去log次，每次O(m)

Insert(dp,i)：是在dp数组当中加入i号物品。

 

void work(int l,int r,int d)
{
    if (l==r)
        for (int i=head[i];i;i=pre[i])
            ans[id[i]]=dp[d-1][S[i]];
    int mid=(l+r)>>1;
    for (int i=0;i<=m;i++)
        dp[d][i]=dp[d-1][i];
    for (int i=mid+1;i<=r;i++)
            insert(dp[d],i);
    work(l,mid,d+1);
    for (int i=0;i<=m;i++)
        dp[d][i]=dp[d-1][i];
    for (int i=l;i<=mid;i++)
        insert(dp[d],i);
    work(mid+1,r,d+1);
}

bzoj22

ftiasch 有 N 个物品, 体积分别是 W1, W2, ..., WN。 由于她的疏忽, 第 i 个物品丢失了。“要使用剩下的 N - 1 物品装满容积为 x 的背包，有几种方法呢？” -- 这是经典的问题了。

她把答案记为 Count(i, x) ，想要得到所有1 <= i <= N, 1 <= x <= M的 Count(i, x) 表格。

N,M<=3000

设f[x]表示全部物品都可用恰好装满x体积时的方案数，可以用01背包算法求出。这是总方案数。
然后考虑不选某物品的情况。

设g[x]为不选当前物品恰好装满x体积时的方案数。

当x小于w[i]时，i物品一定不会被选上 g[i]=f[i]。

当x大于等于w[i]时，i物品可能会被选上，直接求不选的情况比较困难。

总方案数及f[x]，不选的方案数可以想为先不选i再最后把i选上,即g[x-w[i]]。

所以g[x]=f[x]-g[x-w[i]]，x从小到大枚举计算g即可。

每次都是线性复杂度，一共n次计算，总复杂度是O(n*m)

整数划分模型

一类整数划分问题

1：求把n划分成k个正整数的方案数？

2：求把n划分成互不相同k个正整数的方案数？

3：求把n划分成k个不大于m的互不相同正整数的方案数？

4：求把n划分成k个奇数的方案数？

求把n划分成k个正整数的方案数：暴力dp

设dp[i][j][sum]前i个数，选了j个数，和为sum的方案数是多少，答案就是dp[n][k][n]，考虑这一个数选几个来转移即可。这个状态是n*k*n的转移O(sum/i)。均摊O(n*k*n*log(n))复杂度有些高。

本质是个完全背包的，那种写法的话可以做到O(n*k*n)

求把n划分成k个正整数的方案数。

我们直接设dp[i][j]表示把i划分成j个数的方案数。

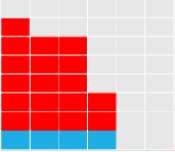
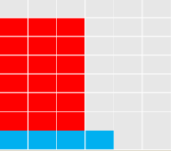
我们可以得到dp[i][j]=dp[i-j][j]+dp[i-1][j-1]。以下是dp[22][4]的两类情况：

考虑有没有1的部分。

我们考虑数形结合来理解。

考虑去掉蓝色的部分。

左图代表：dp[i-j][j]

右图代表：dp[i-1][j-1]

求把n划分成互不相同k个正整数的方案数：暴力

暴力dp:设dp[i][j][sum]前i个数，选了j个数，和为sum的方案数是多少，答案就是dp[n][k][n]，考虑下一个数选不选来转移即可。

本质是个0/1背包， 复杂度O(n*k*n)

求把n划分成互不相同的k个正整数的方案数。

正解也是大同小异。

我们还是直接设dp[i][j]表示把i划分成j个数的方案数。

我们可以得到dp[i][j]=dp[i-j][j]+dp[i-j][j-1]。考虑去掉蓝色的部分。

左图代表：dp[i-j][j]

右图代表：dp[i-j][j-1]

与上一题不同这里第一维

是[i-j]，因为要限制没有相

同的数字。

这里复杂度比上题更低！！

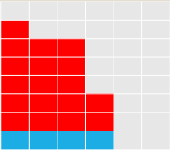
（图片有误，应该互不相同）

复杂度O（n√n）

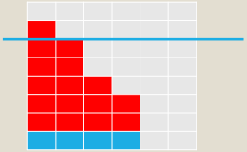
求把n划分成k个不大于m的互不相同正整数的方案数。

背包dp的方法同上。

N=20,k=4,m=6的不合法方案如图。

dp[i][j]=dp[i-j][j]+dp[i-j][j-1]-dp[i-(m+1)][j-1]

减的这一项就是超过线的那种情况。

BZOJ 3612

给定一个杠杆，等距均匀分布一共2n+1个等重质点，支点在n+1处，求拿走k个质点后使杠杆仍然保持平衡的方案数 mod p的值。

1 <= n <= 10000，1 <= k <= 10，2 <= p <= 10000，且 k <= 2n+1

其实就是-n~n中求选k个不同的数，和为0的方案数。

显然求出来f[i][j]表示选出j个数和为i的方案数，然后枚举其中一端拿走几个a，以及拿走的数的重量之和x，把f[x][a]*f[x][k-a]累加之和就是最后的答案了。

这里j个数是互不相同的，也就转化成了我们的“把n划分成互不相同k个正整数的方案数”

算f的复杂度和统计答案的复杂度均是O(n*k*k)。

由此类问题对状态转移的一点感触

dp问题中，转移就是分情况讨论，每种情况对应一个方案数或最优值，而这个方案数或最优值可以表示为之前已经求出来的dp值的组合。

只不过分情况讨论可能方法很多，以一种方式讨论能转化为已知的dp值的叠加，另一种方式也可以。我们需要保证的是：讨论不漏掉任何情况，像计数问题也不能出现方案重叠（求max和min其实是可以重叠的），同时选择分类项数尽量少的方案，以便得到更优的复杂度。

上面几道题的转移方式可能没有原先一些问题的分类方式直观，但是也的确满足了不重不漏尽量简洁的条件。当然这可能也并非是唯一的转移方式，只要保证能划归到之前已经求出的dp值就行。 

数位DP

经典的数位Dp是要求统计符合限制的数字的个数

HDU3652

统计区间 [1,n] 中含有 '13' 且模 13 为 0 的数字有多少个。

考虑填数，一步一步的去填，则必有一位是3

暴力的去枚举每一个数然后去计算必然太慢。

我们先来考虑一个更简单的形式

统计区间 [1,n] 中含有 '3' 的数字有多少个。

N=x_1 x_2 x_3 x_4….. x_total 。 x_i为n的从高到低第i位是多少。Total是总的位数。

如果我们考虑从高到低位不断填数y_1 y_2 …。那么问题其实就是问有多少填数的方案，一要满足上限的限制（对应区间[1,n]），二要满足题目的其他限制。

这样其实就比[1,n]看起来更能dp了。

假设到了第k位y_k!=x_k，则k位之后就没有上限的限制了，情况就简化了。

如果前面y中没有出现3：那么假如我们可以求出来，f[k][0]表示k位之后没有上限限制（随意填），但是必须填个3（前面没有出现），有多少种填数的方案。

如果前面y中出现了3：那么假如我们可以求出来，f[k][1]表示k位之后没有上限限制（随意填），没有必须出现3的限制（前面出现过了），有多少种填数的方案。

首先我们可以枚举到哪一位y_k!=x_k，然后再枚举这一位是多少，把对应的F加起来就是答案了，一共需要加 位数*10 次。这运算次数是不大的。

而f数组总大小也很小，位数*2。

边界 f[total+1][0]=0,f[total+1][1]=1,转移复杂度O(10)

那回归到原题呢？

枚举哪一位不同没什么变化吧，跟原先一样枚举就好了。

就是f数组要变，因为约束条件更多了，所以状态的维数要增加。

设f[k][前面是否已经出现13][上一位是否是1][前面的那些数mod13等于多少],转移的话同样还是枚举这一位是填什么即可。

int dfs(int i,bool state,bool have,int k,bool limit)
{
    if (i==0&&k==0&&have)
        return 1;
    if (i==0)
        return 0;
    if (!limit&&f[i][state][have][k]!=-1)
        return f[i][state][have][k];
    int up=limit?li[i]:9,ans=0;
    for (int j=0;j<=up;j++)
    {
        int h=(k+j*remain[i])%13;
        ans+=dfs(i-1,j==1?true:false,have||(state&&j==3)?true:false,h,limit&&j==up?true:false);
    }
    if (!limit)
        f[i][state][have][k]=ans;
    return ans;
}

Dp经验
1：注意很多时候带进去是n==0要特殊处理。

2：还有一般问[m,n]，我们求[1,n]-[1,m-1]但是有的时候m为0就炸了。然后一道题wa一个小时。。。。。。正常。。。。。

3：求所有包含49的数，其实就是（总数-所有不包含49的数）。前者的化需要有两维限制，一个是上一位是什么，一个是之前有没有49。但是后者只需要记一个上一位是什么。就能好写一些。

4：一般问题的数位dp部分，都是套路，但是这并不代表它外面“华丽的外衣”和与其他算法结合的的部分也是无脑的。要看出它是考数位dp，要看出问题怎么变化一下就是数位dp了。

5：dp初始化memset要置为-1。不能置为0！！！！！！因为有很多时候dp值就应该是0，然后我们如果误以为是因为之前没有计算，从新计算的话，就会tle。

if (!limit&&f[i][state][have][k]!=-1)
        return f[i][state][have][k];

这里不能写成0。

6：既然是记忆化搜索，那就可以剪枝！！！！可行性剪枝！！

7：注意windy数的情况，有时前导0也需要记的！！！

hdu3079

题中平衡数的定义： 以一个位置作为平衡轴，然后左右其他数字本身大小作为重量，到平衡轴的距离作为权值，实现左右平衡（即杠杆原理平衡）。然后为区间[x,y]内平衡数的个数。 (0≤x≤y≤1018)

这题就是典型的 枚举+数位dp

首先，感觉这道题如果记录 当前位、选没选平衡轴、当前左边平衡干权值减右边平衡杆权值，这样感觉并不好转移。而分析题目性质可以发现，

一个非0数只能会有一个（一一对应）平衡轴（0除外，最后特殊处理一下就好），那么如果数位dp外面枚举平衡轴的话，只需计算到最后差是否为0就好。因为每一种中心轴对应的合法集合互不相交

注意0的特殊情况：就是0被统计了位数次，减掉即可。

bzoj3209

设 sum(i) 表示 i 的二进制表示中 1 的个数。给出一个正整数 N ，花神要问你派(Sum(i)),也就是 sum(1)—sum(N) 的乘积。答案对一个质数取模。

对于 100% 的数据，N≤10^15

虽然输入的10进制数，但是本质有影响的是二进制形态

怎么来转换一下，求1~n中每个数的一的个数总相乘之积，首先感觉到，每个数都会有唯一对应的1的个数，且一的个数的取值不到60，因为n最大 10^15, 那么我就想，如果枚举1的个数k，计算有多少个数含有k个1，（因为数位dp就是来做，有多少满足的数，且不关注数的大小）这样就转化为数位dp的模型了另外，发现含有k个1的数个数可能非常多，快速幂搞一搞啦

这题的关键就是发现一的个数的情况比较少可以枚举再转化为另一种情况计算其实，这题本质就是转化一下，注意在模型难以建立的情况下，通过转化，可以将题目简化。

bzoj4521: [Cqoi2016]手机

数字L到R中有多少个数字满足以下两个条件。

1：要出现至少3个相邻的相同数字

2：号码中不能同时出现8和4。

10^10 < = L < = R < 10^11

dfs(i, same, last, appear, occur8, occur4, limit)

Same:上一位和上上一位是否相同

Last:上一位数字

Appear:连续三个相同是否出现过。

Occur4：4是否出现过？

Occur8：8是否出现过？

总结

10进制数位dp的基本最简单的形式。

记忆化搜索处理数位dp的代码实现，数位dp一般都用记忆化搜索来做。

考察思维的数位dp往往会和其他如枚举算法结合，或作为原问题的子问题。

除了十进制，二进制的数位dp也是常见的，此外K进制的也是可以的。

树形DP

树上最大独立集

给你一棵大小为n的树，求这棵树的最大独立集是多少。

最大独立集指的是一个最大的点集使得其中的点两两没有边相连。

N<=100000

dp[i][0/1]表示做完了i的子树，i点是否选的最大独立集，即可直接转移。

 

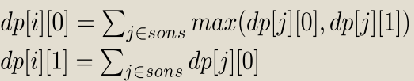
int dfs(int u,int F)
{
    dp[u][1]=1;
    for (int i=hd[u];i;i=pr[i])
        if (to[i]!=F)
        {
            dfs(to[i],u);
            dp[u][1]+=dp[to[i]][0];
            dp[u][0]+=max(dp[to[i]][0],dp[to[i]][1]);
        }
}

树的直径

给你一颗点数为n的树，让你求这棵树的直径是多少，也就是求最长的两个点之间的距离。

N<=100000

1：设f[i]表示i这个点到子树里面的最远点是多远的，然后对于每一个点u求出求出以这个点为根的最远路径距离，直接找{f[son_i]+edge_i}的前两大值加起来即可。然后再在每一个点构成的答案里面取最大值就是全局的最优值了。

2：随便找一个点bfs求它的最远点，设为x，再从x跑一遍bfs，求x最远点y，则(x,y)就是一个直径了。

其他的一些简单问题

1：一棵无向树，结点为n(<=10,000)，删除哪些结点可以使得新图中每一棵树结点数小于等于n/2。也就是求重心。

2：树的覆盖集，求最少选几个点能覆盖所有边，也就是不存在一条边两边点都没被选。（本质？）

3：最大权独立集？

Tree chain problem

给定一棵有n 个点的树，以及m 条树链，其中第i 条树链的价值为wi，请选择一些没有公共点的树链，使得价值和最大。

1≤n,m≤1000

树链就是两个点到lca再拐下去的路径

考虑树形DP，设f(x)为以x为根的子树内选取不相交树链的价值和的最大值，枚举一条LCA为x 的链(u,v,w)，那么当前方案的价值为w+ 去除u 到v 路径上的点后深度最小的点的f的和。

BZOJ1864 三色二叉树

给出了一棵二叉树，点数为n，然后要求每个点和其左儿子和其右儿子三者两两之间颜色互不相同，求最多能有多少点被染成绿色。

N<=10^5

f[i][0] ，f[i][1]，f[i][2]分别表示根是绿红蓝三种颜色时的最多/最少绿色的数量，转移的时候只要保证上面的约束就行，并不难。

int dfsmx(int u)
{
    if(u==0)
        return;
    int l=ch[u][0],r=ch[u][1];
    dfsmx(l);
    dfsmx(r);
    f[u][0]=max(f[l][1]+f[r][2],f[l][2]+f[r][1])+1;
    f[u][1]=max(f[l][0]+f[r][2],f[l][2]+f[r][0]);
    f[u][2]=max(f[l][0]+f[r][1],f[l][1]+f[r][0]);
}

bzoj2466

图论中的树为一个无环的无向图。给定一棵树，每个节点有一盏指示灯和一个按钮。如果节点的按扭被按了，那么该节点的灯会从熄灭变为点亮（当按之前是熄灭的），或者从点亮到熄灭（当按之前是点亮的）。并且该节点的直接邻居也发生同样的变化。开始的时候，所有的指示灯都是熄灭的。请编程计算最少要按多少次按钮，才能让所有节点的指示灯变为点亮状态。

对于100%的数据，满足1 <= n <=100

状态：

f[pos][bool] 表示按下这个pos点的按钮之后，这个点亮(或不亮)，它的所有子孙都亮的最小代价。

g[pos][bool]表示不按这个点的按钮，这个点亮(不亮)，它的所有子孙都亮的最小代价。

树上背包简化版

给出一棵n个点的有根树，每个节点都是一个物品，具有价值Vi，如果一个物品要被选择，那么它的父亲必须被选择。

f[i][j]表示在以i为根子树中选择，i强制选择，选择j个点的最大价值，转移时每次将一个孩子暴力合并到父亲上，合并就枚举这个孩子内部选择了多少点即可。

F[i][j]=max{f[i][j-k]+f[son][k] |k=0…(j-1)}，就是枚举son内选了多少点。

我们按照一般的分析复杂度的方式的话是：状态数N^2*转移复杂度N，总复杂度是O(N^3)。

实际上我们考虑每次合并的时候相当于是一组点对数量的复杂度，总的来看的话就是n个点点对的数量，均摊复杂度O(N^2)。

bzoj4033: 树上染色

有一棵点数为N的树，树边有边权。给你一个在0~N之内的正整数K，你要在这棵树中选择K个点，将其染成黑色，并将其他的N-K个点染成白色。将所有点染色后，你会获得黑点两两之间的距离加上白点两两之间距离的和的收益。

问收益最大值是多少。

N<=1000

定义状态f[i][j]表示i号节点为根节点的子树里面有j个黑色节点时最大的贡献值

void dfs(int u,int fa,ll dis)
{
    size[u]=1;
    for (int v,i=head[u];i;i=edge[i].pre)
        if((v=edge[i].to)!=fa)
        {
            dfs(v,u,edge[i].dis);
            for (int j=size[u];j>=0;j--)
                for (int k=size[v];k>=0;k--)
                    f[u][j+k]=max(f[u][j+k],f[u][j]+f[v][k]);
            size[u]+=size[v];
        }
    for (int i=0;i<=size[u];i++)
        f[u][i]+=dis*i*(k-i)+dis*(size[u]-i)*(n-size[u]-(k-i));
}

树上背包

给出一棵n个点的有根树，每个节点都是一个物品，具有价值Vi和重量Wi，如果一个物品要被选择，那么它的父亲必须被选择。

在dfs序上Dp，如果不选一个点，则跳过代表他的子树的dfs上连续一段。

设f[i][j]表示dfs序上第i个点到第n个点，选了j的重量得到的最大的价值是多少。i可以选也可以不选。不选的话就要跳过整个子树。

设T[i]表示dfs序为i的点标号。

不选：f[i + size[ T[i] ] ][j]

选：f[i+1][ j- w[ T[i] ]]+v[ T[i] ]

两种情况取最大值即可。

另一个奇妙的方法

不是每次将孩子与自己合并，我们直接把dp数组复制再传给孩子，再从孩子递归下去，最后原来自己的Dp数组和孩子的Dp数组直接在对应重量的价值中取max。

以下是步骤：

我们现在在u节点，对u节点的dp数组中加入u点的物品。

做dp[i]=dp[i-w[u]]+v[u]操作，表示强制加入了u这个物品。

Dpson数组=dp数组。

递归计算son的dp值，传入的参数是dpson数组。

回溯回u点

对每一个i做dp[i] = max{dpson[i],dp[i]}

bzoj5123

求一棵 [1,n] 的线段树的最大匹配数目与方案数。

树形dp+记忆化搜索

设 f[l][r] 表示根节点为 [l,r] 的线段树，匹配选择根节点的最大匹配&方案数，g[l][r] 表示根节点为 [l,r] 的线段树，匹配不选择根节点的最大匹配&方案数。那么这是一个很普通的树形dp。

注意到区间长度相等的线段树的结果是一样的，且每层至多有两种区间长度不同的区间(打表或者推推式子都行)，因此直接以区间长度为状态进行记忆化搜索即可。

基环树

基环树，也是环套树，简单地讲就是树上再加一条边。

如果把那个环视为中心，可看成：有一个环，环上每个点都有一棵子树的形式。

因此，对基环树的处理两部分分别为对树处理和对环处理。

基环树问题处理方法

处理方法有

1：断开环上一条边，枚举边端点的情况，然后当树来处理。

2：先把环上挂着的树的信息都计算完，然后转化为序列问题，或者说是环形的序列问题。

dfs找环

基环树，环是关键，所以做这类题目我们首先得找到环。

找环的方式很多，这里讲解dfs找环。 ◦对于dfs找环，我们就对这个基环树做dfs遍历。我们知道对于一个在图， 它dfs树上的每一个返祖边(vàu)， 和dfs树上构成的路径就会构成一个环。也就是我们只需要找到这个返祖边即可。

void dfs(int u,int F)
{
    fa[u]=F;
    vis[u]=true;
    for (int i=hd[u];i;i=pr[i])
    {
        if (to[i]==F)
            F=-1,continue;
        if (!vis[to[i]])
            dfs(to[i],u);
        else
        {
            int tmp=u;
            circle[cnt=1]=u;
            do
            {
                tmp=fa[tmp];
                circle[++cnt]=tmp;
            }while (v!=tmp);
            found=true;
            return;
        }
        if (found)
            return;
    }
}

主函数调用时，要枚举每一个点。

for (int i=1;i<=n;i++)
    if(!vis[u])
        dfs(i,0);

因为有可能是个基环树森林。

这是很容易犯的一个坑：n个点n条边不一定是个基环树，准确来讲是基环树森林！！

如果说我们要采用断开一条边，当成树来处理。我们不需要找出来整个环，只需要找一个在环上的边，按下图写法会简便很多。

void circle(int u,int f)
{
    b[u]=true;
    for (int i=head[i];i;i=pre[i])
    {
        int v=to[i];
        if (f==v)
            f=-1,continue;
        if (b[v])
            if (rt1==0)
                rt1=u,rt2=v,continue;
        circle(v,u);
    }
}

基环树内向

首先它是一个有向图，它构成类似基环树的结构，有一个特点是每个点都有且只有一个出度，并且环外的节点方向指向环内。

如果题目说满足每一个点都有一个唯一出度，则本质上就是给了我们一个基环内向树森林（不只是一个基环内向树！！！！）

任何一个点沿着唯一出边走都会走到环上

利用这个性质可以随便选一个点再通过一个简单循环找到基环树的环。

基环树外向

与基环内向树相反，它有且只有一个入度（基环内向树是出度），并且由环指向环外。

可以把所有边反向后，变成基环内向树找快速找环。

bzoj1040

N个人，每个人都有一个战斗力和一个讨厌的人（不是他本身），要求一个总战斗力最大的人的集合，满足集合内部两两不互相讨厌

N<=10^5

把这个讨厌关系的图画出来，就是个基环内向树森林，然后我们要求最大权独立集。

dfs函数：就是求一个最大权独立集，与树上的并无大的区别

work函数：枚举断开的这条边，那一端点强制不选，取最优值

void dfs(int u,int fat)
{
    f[u][0]=0;
    f[u][1]=val[u];
    for (int i=head[u];i;i=pre[i])
        if (to[i]!=rt)
        {
            int v=to[i];
            if (fat==v)
                fat=-1,continue;
            dfs(v,u);
            f[u][0]+=max(f[v][0],f[v][1]);
            f[u][1]+=f[v][0];
        }
}
ll work()
{
    ll ans=0;
    for (int i=1;i<=n;i++)
        if (!b[i])
        {
            rt1=rt2=0;
            circle(i,0);
            ll kk=0;
            rt=rt1;
            dfs(rt1,rt2);
            kk=f[rt1][0];
            rt=rt2;
            dfs(rt2,rt1);
            kk=max(kk,f[rt2][0];
            ans+=kk;
        }
    return ans;
}

下面是避免环长为2的特殊情况，出bug。

if (fat==v)
    fat=-1,continue;

BZOJ1791

求无向基环森林中的每棵基环树的直径之和。点数n<=10^6

先找出环，很明显答案有两种情况。

1：在以一个环上节点为根的向外的树的直径。

2：以两个环上节点分别为根的最大深度再加上两个节点在环上距离。

第一种情况就是之前讲的树形dp。

第二种情况要处理出以环上每个节点为根的最大深度d[i]，环上的点重标号，选环上1号点作为基准点，求出s[i]表示i号点到1号点的距离，sum为总的环长。设我们找的两个环上节点是i,j则max( min{s[i]-s[j],sum-(s[i]-s[j]} +d[i]+d[j])即为所求，但如果暴力求是n^2的。并没有比最开始直接枚举快多少。

考虑优化（单调队列）

我们考虑把内部的一个min去掉，式子能看起来更清晰一些。

max( min{s[i]-s[j],sum-(s[i]-s[j])} +d[i]+d[j])

max (  1: s[i]-s[j] +d[i]+d[j] | s[j]>=s[i]-sum/2,

2: sum-s[i]+s[j] +d[i]+d[j] | s[j]< s[i]-sum/2 )

考虑枚举选的两个点的后一个点i，然后求对于i，离i最远的j距离是多少，然后对于每一个i的答案求最大值就是整个基环树的直径了。

第一种情况s[j]>=s[i]-sum/2 ：求d[j]-s[j]的最大值即可，注意可选的j区间会移动，所以这里需要单调队列。

第二种情况s[j]< s[i]-sum/2：这个可行区间只会变大，不会缩小，所以直接记录s[j]+d[j]的最大值即可。