BillBoard 的简单教程（译）(原创)

BillBoard 的简单教程（译）

作者：Antonio 译：goku_1

译注：

翻译水平有限，建议看原文：http://www.lighthouse3d.com/opengl/billboarding/index.php?billCheat2 Billboarding Tutorial 

As mentioned before to get a cheating version of a billboard it is enough to reverse the orientations of the top3x3 submatrix from the modelview matrix. The previous sections achieved this by setting this submatrix suchthat the appropriate transformations were reversed.

正如我之前提到的关于一个制作billboard的巧妙方法，这个方法只用反转模型视图矩阵（modelview matrix）
的前3x3 子矩阵。前面的教程用适当的对子矩阵的变换实现了这个方法。

In here an alternative approach is presented. This is also a popular approach, it even got mentionedin the book OpenGL Game Programming. 

现在我提供另外一个流行的方法，这个方法曾在《OpenGL Game Programming》书中提及。

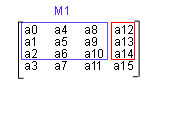
The vertices of the billboard are defined using up and right vectors that reverse the orientations ofthe modelview matrix. These vectors can be extracted from the inverse of M1.

Billboard的顶点被完全定义，经过模型视图矩阵的反转得来的右向量（right vectors)。
这些向量可以从经过反转的M1举证中提取出来。（译注：这段不太理解字面的意思，不过大体意思是，
可以从M1矩阵中提取出一个右向量和定义billboard各个顶点的信息，具体在后文介绍）

Fortunately, for an orthogonal matrix, the inverse is equal to the transpose. Is M1 orthogonal?It should be. If you're only using gluLookAt to perform you're camera movements, or just doingtranslations and rotations to the camera, then M1 is orthogonal. If, on the other hand you mess aroundwith the modelview matrix then you may end up with M1 not being orthogonal. 

幸运的是，对于一个正交矩阵，反转它等于求他的转置。M1是正交的吗？它是的。如果你只是使用
gluLookAt 函数来执行摄像机的移动，或者只是移动（translations）和旋转（rotations）摄像机，
那么M1就是正交的。另一方面假如你瞎搞模型视图矩阵（modelview matrix）的话那么你的M1有可能就不是正交的了。

Just in case you're wondering what the $%*# is a transpose, a matrix A is a tranpose of B, AT = B, if aij = bji, for every element. 

以防你对什么是“转置”觉得奇怪，在此简要介绍一下：A矩阵是B矩阵的转置，哪么AT=B, 对于所有元素aij = bji。
（译注：不知道转置就GOOGLE去，这里解释的不清楚）

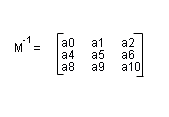
So what is an orthogonal matriAs mentioned before a square matrix Q is orthogonal if Q x QT = I, where QT is the
 transpose of Q and I is the identity matrix. In practice this means that the multiplying any two different columnsor rows returns zero. This means that the cross product is zero, and therefore that the vectors are at right angles. It also means that multiplying a vector by itself should give 1, i.e. the vectors are normalized. So now that you know you can write

 your own routine to see if a matrix is orthogonal.

结果是一个正交矩阵吗？正如前面所提到的一个方矩阵Q是正交的，如果 Q x QT = I QT是Q的转置，I是单位矩阵。 

在实践中这意味着两个不同的列或行相乘返回0。还这意味着叉乘为0，因此两向量（译注：矩阵中的行列代表的向量）相互垂直。

这也意味着一个向量乘它自己会得到1， 例如，向量是单位向量，那么现在你可以写一段代码来得知这个矩阵是不是正交的。

So we can easily get the inverse of M1. The first column of the inverse of M1 is the required right vector, and the second column represents the up required vector.  

我们可以很轻易的反转M1矩阵。反转M1矩阵后的第一列是我们需要的右向量（right vector）,第二列是我们需要的上向量（up vector）。

right =    [a0,a4,a8]

up  =    [a1,a5,a9]

Two examples of a quad billboard are now presented to show how to define the vertices. Assume that the quads edges have a length size.

两个关于四边形billboard的例子将展示如何定义billboard的顶点。假定四边形的边缘是有长度的。

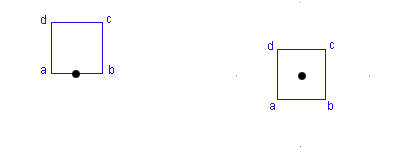
First a quad with the center at the bottom origin is presented (left figure).  

首先是一个中心点在底部的四边形四个顶点的计算公式（左图）。

a = center - right * (size * 0.5);

b = center + right * size * 0.5;

c = center + right * size * 0.5 + up * size;

d = center - right * size * 0.5 + up * size;

The right figure represents a quad with a centre on the middle of the quad. Its vertices are defined as:  

右图展示了一个中心点位于中心的四边形。它的四个顶点如下定义：

a = center - (right + up) * size;

b = center + (right - up) * size;

c = center + (right + up) * size;

d = center - (right - up) * size;

When compared to the previous method you only get the modelview matrix once per frame. On the other hand you have tomanually transform the vertices of the billboard. Overall this method is faster for quads, only 4 vertices, but harder to implement.If however you try to billboard an object with a larger number of vertices then the previous method could perform better.

（译注： 不太懂，貌似是说比较前几个作者的教程里所说的方法。 前面的方法可能是用了多个顶点的计算，导致前面的方法在

四边形billboard上效率低下， 但是如果对于有很多顶点的billboard用作者前几个教程的方法，将会更好。）

In the source code a function is provided to extract the up and right vectors  

在下面的代码中，这个函数可以提取向上的向量(up vectors)和向右(right vectors)的向量。

void l3dBillboardGetUpRightVector(float *up, float *right); 

Parameters:

 

up - an array of 3 floats. The function sets this to be the up vector

right - an array of 3 floats. The function sets this to be the right vector

The source code is as follows: 

完整的提取向右向上的代码如下：

void l3dBillboardGetUpRightVector(float *up,float *right) {

    float modelview[16];

    glGetFloatv(GL_MODELVIEW_MATRIX, modelview);

    right[0] = modelview[0];

    right[1] = modelview[4];

    right[2] = modelview[8];

    up[0] = modelview[1];

    up[1] = modelview[5];

    up[2] = modelview[9];

} 

If what you're after is the cylindrical version of this method then just set the up vector to [0,1,0]. You can use the function l3dBillboardGetRightVector, provided in the source code, to get the right vector. 

如果你想使你的billboard只想饶着y轴转，那么你只要使你的上向量（up vector)等于[0, 1, 0]. 你可以自己写

一个l3dBillboardGetRightVector 函数来实现，在此函数里只要提供获取右向量的代码。