一句话题解(2021.2&3)
7022. 2021.03.19【2021省赛模拟】词典 (dictionary)
显然每次把左边放01右边放1下面接两个子树,f(i)=C(i)+min(f(j)+f(i-j)+C(j))
发现是闵可夫斯基和,且由于C是nlog级别所以f是nlog^2级别,差是log^2级别
暴力小数据,倍增(log)每次1.2倍求出差的分界点(log^2),求某个值就三分(log)+二分(log)已知段,总时间O(log^5)
7021. 2021.03.19【2021省赛模拟】整除 (div)
求和判掉x=1,变为判是否模x^m-1
枚举x,每次可以把系数>=x的变一个x出来,直接暴力搞堆维护即可,总势能为nlnn,时间O(nlnnlogn)
注意系数全为x-1或全为1-x时也是0
7020. 2021.03.19【2021省赛模拟】圆弧 (arc)
把一个1转到开头变成链,dp设f[i]表示到第i位的答案,转移根据当前是前面的还是后面的维护,有一些情况不能转移所以要用线段树维护限制
题解做法是直接求最大个数的方案,由于最大为n所以直接扫即可
6082. 【GDOI2019模拟2019.3.25】染色问题
反着搞,等于把m-1种颜色往里面插,每次插一段乘上(当前个数+1)
把初始长度+1,等于每次乘上加入前长度,把第一次的1去掉就是每多加一个非m颜色就会乘上新的长度,即\(\prod_{i>=2} (x+i)\)(把ix+1反过来更好搞)
直接分治ntt,右边就把(x+mid)^i卷出来
7029. 2021.3.27CCF NOI Online 能力测试提高组第一题 愤怒的小 N
发现要算的是popc(i)为奇数的,直接数位dp暴力nk^2搞有60
维护一下奇-偶,则一个结论是当n>K时2^n奇偶相减为0

给(1-x)(1-x^2)...代入e^x,发现每多乘一项少一个x,直接从n-K位开始dp,总和插值算
PE753 Fermat Equation
打表发现当p%3!=1时出现次数全为1,p%3=1时出现次数为0或3,所以可以固定一个O(p)算然后乘个数,这样可以O(p^2/log)
然后跑了9h爆了过去
证明:当p%3=2,(p-1)%3=1,所以3在模p-1意义下有逆元,因此可以把一个数变为p原根g的3i次方,把3i模p-1,3可以除掉,得到的指数互不相同,因此原数模p互不相同;p%3=1则会按k=(p-1)/3分组,每组恰好是i,i+k,i+2k三个
当p%3=1时有神必定理:
当p为质数且\(p \equiv 1 \pmod 3\)时,存在恰好一对\(AB\)满足\(A\equiv 1 \pmod 3\),\(B\geq0\),\(4p=A^2+27B^2\)
则\(x^3+y^3\equiv 1 \pmod p\)的解的对数为\(p-2+A\)
把c除过去求x,y≠0的解,证明A Classical Introduction to Modern Number Theory里面有
所以暴力枚举√p个B判断即可1s内出解
code:https://gmoj.net/senior/#main/code/829442
7034. 2021.03.28【2021省赛模拟】道路的眼泪(tearroad)
按点从大到小连并查集,连出来一棵以1为根的树,则Vi就是i到1路径上的点
问题1直接枚举算,问题2树上连通块dp,问题3选择不同结果不同(否则异或为空但有操作),所以是C(n,i)
7033. 2021.03.28【2021省赛模拟】超命运树 (destsurr)
丢到笛卡尔树上,发现f(S)=1当且仅当虚树建出后非叶=叶-1=|S|-1,即没有x选x的两个子树都选,Len=非叶=|S|-1,dis就是算S的Len相同的超集(f不用为1),即新加一些点后没有新增非叶
直接dp,设f[i]表示i的答案,转移分类讨论
①只有一个儿子选
1、超集另一边不选,所以i可选可不选,且超集的选择相同
2、超集另一边选(只放一个所以乘size),所以i必选否则Len不对
②两个儿子选
i必不能选否则f不对,超集可选可不选
直接dfs会爆空间,反着扫即可
7032. 2021.03.28【2021省赛模拟】制作美食(delidish)
把(y,-by)加到平面里,每次加一个(ax,-x),会把左下角的所有点连起来,排序扫过去堆维护
也可以桶排然后反着做链表维护,每次等于把最后一段和链头相连,一些点过了就删掉,这样可以O(n)
6087. 【GDOI2019模拟2019.3.26】获取名额
先把a和x除以max(a),当1-a/x很小a/x很大时暴力找,最多log个爆精度
当a/x很小时取ln,把ln(1-a/x)在t=a/x=0处泰勒展开变成Σ-(a/x)^i/i,线段树维护一下log项
6086. 【GDOI2019模拟2019.3.26】动态半平面交
没有在线数据,深度<=d可以离线按bfs序搞,每次直接询问子树和,在线就加个可持久化
贡献就动态维护p^k的虚树,每次把相邻两个加lca减
6085. 【GDOI2019模拟2019.3.26】要换换名字
暴力找边+二分图匹配,根据hall定理只用保留n条,如果按位加然后不断流即可不用二分
CF1498E. Two Houses
无询问:按度数排序,则前i个的度数至少为i(i-1)/2,如果sum=i(i-1)/2就是一个强连通分量,找出来后直接算
7037. 2021.03.30【2021省赛模拟】打扫笛卡尔 (cartesian)
水题
设f[i]表示期望dep和,g[i]表示期望个数和,发现往下走的概率为直接走(1/3)+走另一边再走(1/6)=1/2,枚举一边size卷积,算的时候要乘上另一边的方案数
拆拆画画即可前缀和O(n)无逆元
7036. 2021.03.30【2021省赛模拟】凌乱平衡树 (treap)
发现最后的合并操作等于把1树右链和2树左链拉出来按照size归并,排序后的每个点会使size小于它的另一个树的点深度+1,即ans加上后继的size
动态维护,每次rot后改变两个点,注意如果要动态维护前驱后继很麻烦,所以对同一棵树的size差分,贡献为后面的所有和
修改考虑前后的,线段树维护
7035. 2021.03.30【2021省赛模拟】神奇纸牌(uno)
直接压状态矩乘硬冲
或者更暴力搞,每个点有16种连边情况,再枚举2^16的出现集合,并查集判断
arc116F - Deque Game
597上次出的题的超集
先考虑奇数,如果只有3个先手是max(min(a,b),min(b,c)),因为如果A选了一边B跟着选,则这样对B有利所以A一开始会选另一边,这样变为[2,n-1]的子问题
发现双方先选都不优且不改奇偶,所以都不会先选奇数
偶数选一边后变为两个奇数,判断一下最后是谁选所有奇数,双方对偶数操作后会对全选的那个人有影响,根据操作后全选者选的值变为二元组排序选
7028. 2021.03.26【2021省赛模拟】旅行(travel)
枚举第K大的边w,把边W变为max(0,W-w),跑最短路后枚举K加上K*w
当计算的不是第K大时会更劣,如果大于则Kw多加,小于则W-w多加
7027. 2021.03.26【2021省赛模拟】a(a)
枚举余数,则有一些位置会有限制,把限制容斥为全部-无,然后按位dp+前缀和优化
或者按余数分类前缀和也可以
7026. 2021.03.26【2021省赛模拟】序列(sequence)
可以莫队+线段树维护时间做到O(n√nlog),也可以kdtree直接搞
注意kdtree不能建虚点否则会假
CF1286D. LCC
硬点某一对(x,x+1)是第一个相遇的,设f[i,0/1]表示匹配到i方向左/右,矩乘线段树优化即可
题解的mask就是矩阵,但是并不知道所以想用阴间线段树维护
PE670 Colouring a Strip/PE671 Colouring a Loop
670好做,直接矩乘加速f[i,0~3,0~3],表示匹配了多少位
671先Burnside(其实n是质数所以不用),然后变成环了所以加上两维变成f[i,0~3,0~3,0~2,0~2],表示颜色是否与初始的两种相同,直接矩乘+亿点点细节
由于是环所以要枚举一开始两种颜色的长度,比较好写的做法是先乘到max(长1,长2)+1,中途把不合法的情况变为0,再考虑一开始是2*1的情况
code:https://gmoj.net/senior/#main/code/827794
PE742 Minimum area of a convex grid polygon
dp1/4的轮廓线,把<=50的(x,y)=1的向量xy找出来,高度最多到3000即可
code:https://gmoj.net/senior/#main/code/827785
PE741 Binary grid colouring
rk95,好耶
Burnside,变成不动、转90、转180、沿边翻转、沿对角线翻转
①沿边翻转
显然对折后一行放一个,每个放在n/2列中且每列放两个,所以是\(\binom{n}{2,2,2,...}\)
②不动
拆点,变成每次两边各选一个集合进行顺序匹配,发现另一边等于一个排列直接对过去(乘上n!),枚举的那边可以前缀和
③转90
把n/2,只考虑左上1/4部分,则第i行/列的和等于新矩形第i行+第i列,即每选一个点(i,j)会把i+1,j+1(i可以=j)
同②dp,特判加一个点,每次加x(x>1)个点时一定是形成了一个环,同时x条边可以放在右上或左下,所以乘上2^x,前缀和优化
④沿对角线翻转
只考虑右对角线上部分,第i行/列的和等于第i行+第i列,也是每选(i,j)会把i+1,j+1
不同之处在于只有一半所以不能加1/2个点,并且边不能*2,前缀和
还有一种情况就是x自环-y-z自环,这样前缀和时多乘了一个j,所以要用两个sum维护
⑤转180
最阴间的情况
先考虑n为偶数,把下面折上来,则行不变第i列等于i列+(n-i+1)列,再沿n/2把右半折到左边,则此时的情况基本等于n/2的子问题
不同之处在于,一列的两个黑格子可以叠在一起,如果不叠则展开有4种情况
枚举叠了多少个,组合数算一下即可O(n)
再考虑n为奇数,发现((n+1)/2,(n+1)/2)显然不能选,则第(n+1)/2行or列都要选一个,把选了的再横竖划提出来变成九宫格讨论
若九宫格内有其余的,则只能是两个对角,剩下的就是n-3的子问题
如果没有其余的,可以发现此时可以把九宫格合成一个空格子,因为中间行/列去掉了,旁边的上下、左右二合一,就是n-2的子问题
所以如果n为奇数就要求出1n的dp值,直接mtt暴力卷即可爆精度~,直接暴力跑十几分钟即可以了
code:https://gmoj.net/senior/#main/code/827704
arc105D - Odd Degree
如果是一棵树,则选了若干个奇数点后方案唯一(根据每条边两侧点的奇偶考虑),加上非树边后剩下的方案仍唯一,所以乘上2^k*组合数
6084. 【GDOI2019模拟2019.3.25】礼物
burnside,然后对于每段枚举首+尾长度,中间组合数+容斥,暴力枚举是O(Σσ0),把组合数合并变为O(Σσ0/K)
也可以硬点第一个0在首位,然后乘上(长度/0的个数),这样如果没有循环就显然,否则因为算的是确定后不同的,循环不会被考虑同时乘的分子分母按比例减少,不影响结果
PE317 Firecracker
以原点往下为轴展开一个半径为s的圆,再把圆往上拉形成圆柱顶住三维图形,如果求出了高h就可以积分求体积,省略大部分过程后有
\(\large 1/2(2v-gt)t=h\)
\(\large 1/2(2v\sin-gs\sec /v)s\sec=h\)
有\(\large \sec'=\tan\sec\),则
\(h'=\large s/2(2v\sec^2-gs\tan\sec^2 /v)=0\),中间有一步\(\large \tan^2+1=\sec^2\)
解得\(\large \tan=v^2/gs\),代入原式得\(\large h=v^2/2g-gs^2/2v^2\),则最高值\(\large H=v^2/2g\),\(\large s^2=v^4/g^2-2v^2h/g\)
答案\(\large ans=\int_{-100}^{H}\pi(v^4/g^2-2v^2h/g)\)
2021.03.18【2021省赛模拟】皇后
随机调整,每次找一个矛盾最多的,再枚举一个换掉后矛盾最少的换,卡住了就打乱
code:https://gmoj.net/senior/#main/code/826490
7019. 2021.03.18【2021省赛模拟】游戏(game)
发现B一定放在A的较长侧,因此等于求至少有长K=2k-1段的方案
容斥,推导可得\(\large [x^n](1-x)\frac{1}{1-(mx-(m-1)x^k)}\)
当k很大时枚举x^k的次数,lucas暴力算
当k很小时把无穷级数展开(就是求F=1/(1-G),GF+1=F),常系数齐次线性递推
7018. 2021.03.18【2021省赛模拟】光明(light)
长链剖分,再记一个时间来累加,求出桶后直接扫
5669. 【GDSOI2018模拟4.19】排列
最大子段和一定是分成三段,中间选前后不选
所以考虑每个在哪里,连边st->i->i+n->ed,约束就类似二元关系,同一段内因为保证有解所以不用考虑
ans=正-最小割
7011. 2021.03.13【2021省赛模拟】nonintersect
发现2/pi实际就是|sin|的期望,所以随机一条直线把线段投影过去的长度和期望就是2/pi*X,如果有小于就一定有大于,所以一定有解
可以按θ划成n段,每段拆成asin+bcos的形式即可求出最大值,然后把投影左端点当-1右端点+1,这样显然按前后n个分开匹配更优,问题变为求合法匹配
注意一定有解,因为可以用欧几里得距离做最小匹配,显然不会交叉
构造,每次把最左的点找出,找到一个右边的点将其划分成两个能匹配的集合,记录每个点所属的集合即可期望O(nlog^2n)最坏O(n^2log),实际跑不满
7010. 2021.03.13【2021省赛模拟】graph
斯特林反演
7009. 2021.03.13【2021省赛模拟】抽卡(card)
计算抽一次的期望次数,每次算多抽一张的概率,打表
2021.03.15【2021省赛模拟】C
定义solve(x)表示确定x的子树,每次二分一个后继进行solve操作直到遇到叶子
然后对于一个后继全部确定的在叶子集合里二分找
时间分析:前后两次操作类似,每个点被二分1次,判断是否继续时为(要找的+1),即作为找和被找各1次,所以一次操作nlogn+2n,总次数为2nlogn+4n,经过计算发现前面两个log都多了1n的空缺所以能过
code:https://gmoj.net/senior/#main/code/826109
ll的做法:先找叶子,然后每个点二分出编号最大的叶子,等于按叶子从小到大access,之后对每条链排序,再按链编号从小到大二分儿子
总复杂度分析下来是2nlogn+2n且跑不满
7017. 2021.03.15【2021省赛模拟】B (口胡)
长链剖分线段树,用状压每次把最小的连后面的,状态数不多
合并一是要求两个儿子点积,枚举较小者查另一边,总和n每次Dlog
另外要硬点某个继承,如果是轻边就暴力扫,重边就区间乘
7016. 2021.03.16【2021省赛模拟】A
观察发现,如果一个1碰到了另一个1,则其会复刻前面的1的路径并延迟1次,拿栈维护一下,每次加1时前移所以栈里记第几个1
更简单的做法,维护下一个1加入后的操作序列,如果加了0就可以在第一次停下来时缓冲即t-1,加1就第一次停一下
用指针同时维护做到O(n)
7014. 2021.03.15【2021省赛模拟】丰(three)
拆边枚举直径中点,则显然每次加叶子的父亲边,先加到全部相同然后每次f[i]+叶子*2->f[i+1]
换根dp求f再扫一遍,二分找<=2n的后再判2n-1和2n
7013. 2021.03.15【2021省赛模拟】キ (two)
分治算跨过中线的矩形,求f[i,j]表示上i下j的左边答案,枚举i维护h[k,j]表示第i行第k列对j的贡献,把k加一起,i移动时继承再加上新的部分,O(nm)一次
硬点长贡献短,反过来会多算,每次横竖轮流切做到O(n^2log)
7012. 2021.03.15【2021省赛模拟】十 (one)
可以很神必地发现把1看作(0看作)时任意操作从内开始地括号层数集合不变
证明:原来的)等于新的(,只考虑这一种的匹配,把其他的全填满另一种,发现等于每次把每段长-1,与方向无关所以得证
然后用堆+链表维护即可
arc114F - Permutation Division
当a1<=k时显然1~k拆,否则枚举最后一段不动的起点i
由于硬点了下一段一定会变劣,所以要使该段最长,而i固定后前面的要尽量多分,最多分s=|LDS|次,后面分k-s段,a从1加用线段树找后第k-s个即可
注意LDS的起点要为1
arc114E - Paper Cutting 2
等价于四方向确定一个删除排列,如果删的不是前缀最大就忽略
假如放了一个前缀最大值,下一个最大值放的无论是哪个无论在哪里,非前缀最大值的放置情况都互相对应,因此概率是一样的,与题目的操作等价
把大小>=i和选了结束的提出来算,显然相互独立
arc114D - Moving Pieces on Line
比赛时刚E去了,回来发现D是sb题
发现一个点的移动等于在起点和终点各加一个前缀异或,把起点和t丢一起把a排序
发现最后会形成若干间隔,每个间隔点都要有,其余的相邻配对,dp确定每个点的终点即可
CF1500D. Tiles for Bathroom
O(n^2dlogn)的做法:确定左上角二分边长,用倍增搞出2^k大小的矩形,在不能*2时把四个矩形合并判断
gym102511F. Directing Rainfall
先用set+扫描线把线段拓扑排序,然后维护min(a)+b的标记,+b minc=min(c-b)+b
每次对[x,y]+1(x<y)然后对f[x]取min,接着可以向一侧取前缀/后缀min,线段树维护,每次操作势能+log所以应该是O(nlogn)的
CF上注意空间
5680. 【GDOI2018Day2模拟4.21】绝对伏特加
三年之期已到.jpg
显然是求\(\large [\frac{x^n}{n!}] (\sum \frac{i^Fx^i}{i!} )^Le^{(K-L)x}\)
\(=\large [\frac{x^n}{n!}] (\sum_k S[F,k] x^ke^x)^Le^{(K-L)x}\)
\(=\large [\frac{x^n}{n!}] (\sum_k S[F,k] x^k)^Le^{Kx}\)
由于模数很小且\(x^a\)贡献时会乘n的a次下降幂,直接爆算维护mod个即可O(FLmod),或者短多项式求幂做到O(F^2L)
7008. 2021.03.12【2021省赛模拟】威士忌(whiskey)
单调从大到小枚举x,发现yz在x不满足时是向右上的矩形,满足时是向原点矩形的补集,形成一个阶梯
发现不断枚举时有一些会不满足,可以用线段树+set维护,也可以发现从不满足->满足时阶梯可能会新增,但由于当前的变成向右上了所以全部不影响,因此排序后单调队列+双指针维护即可O(n)
7005. 2021.03.11【2021省赛模拟】特立独行的图(graph)
枚举最小点(可以不用),然后分成两段L/2,另一边不断移动时对左边的边集会不断变大且包含
排序+bitset判断,构造的话分成2n一段,把右边点边集大小相同的和左边同时增加的分别压起来,一段里留n的空
注意有三元环的情况,特判一下几种情况
7004. 2021.03.11【2021省赛模拟】洛希极限(roche)
发现只能走x+1或y+1,求出往右/下走多少即可O(n^3)
用单调队列每行/列维护,求走多少步用线段树即可
upd:一开始求往右和往下可以并查集O(nm),之后的单调队列满足右端点不减(矩形包含),所以可以直接搞
如果排序用桶排即可O(q+nm)
gym101471J. Son of Pipe Stream
把f乘v变为f',则f和w等价,答案变为\((fv)^aw^{1-a}/v^a=f'^aw^{1-a}/v^a\)
流出最大F,最大W和最大S=F+W,发现(i,S-i) i∈[S-W,F]都能选到
不考虑方向相同,可以从起点硬点先流哪条边,先流1流完F后剩下就是S-F,W同理,所以(F,S-F)和(S-W,W)可以构造,接着把二者的流量网络按比例取即可得到(i,S-i)
对答案\(f'^aw^{1-a}\)求导得到极值\(f=a*S\),考虑构造一种方向相同的最优解
从1流f2流S-f,接着从3往1退流剩下的就是2了,这样方向一定相同且根据上面的一定有解
gym102482C. Conquer the World
模拟费用流,从下往上维护正负(负的加上-inf保证全部合并),在lca处合并,(x,y)撤销是v'x=2dlca-vy和v'y=2dlca-vx
合并用左偏堆,感觉不能把相同的合起来所以写了O(xlogx)
注意左偏堆要不断维护根节点,因为不能保证最大深度
CF1495D. BFS Trees
枚举xy,路径外的点一定只能连fx,i fy,i同时-1的点,乘起来即可
CF1495C. Garden of the Sun
每三行全选,剩下的两行间隔补一下
gym101630I. Interactive Sort
数据随机(不随机可以打乱),所以每次把一个偶数在奇数段里二分,先二分整段再暴力扫,每次最多扫两段同时多一段,扫完后即可求得当前偶数的值,搞完后奇数也排好序了
期望次数应该是O(nlogn)
gym100307D. Dictionary
发现不存在两条链先接起来然后另一条链接上去的情况,全部都可以用一条链接到另一条上来表示
建图跑朱刘算法
7001. 2021.03.09【2021省赛模拟】续命大战(extension)
设剩下的势能为Σ2*每个数+1,则结果与奇偶有关
发现只有1操作删多个偶数时会改变,因此先把奇数位的去掉(sg=0/1),然后对每个偶数独立算sg
考虑偶数a,发现sg_a(x)当x%(a+1)=a时为2否则为(x%(a+1))%2,证明递推归纳
7000. 2021.03.08【2021省赛模拟】统计(count)
树分块y所在块,然后fft x,z都不在块内的,有一个/两个在外的直接暴力
如果链剖+分块log会在外面,卡卡就过了
6999. 2021.03.08【2021省赛模拟】递推 (recurrence)
发现实际就是复数乘法,每次乘x+yi
要求a+bi的ab,有\((x+yi)^n=a+bi\),\((x+yi)^{2n}=a^2-b^2+2abi\),等于求\(1/2\sum \frac{(x+yi)^{2k}}{C^k}\)的虚部
直接等比数列求和,m非无穷就判C%p,无穷化式子发现只要xy非0就一定不error
复数除就把模长取倒再取共轭
6998. 2021.03.08【2021省赛模拟】序列 (sequence)
设f[i,j]表示考虑前i段答案为j的最大sum,中间用堆贪心一下即可
agc052
A:直接n个0+n个1+0即可,若s[n]为0则显然,否则找到前面的第一个0,中间的1可以在第一个s时匹配掉
B:新建虚点连1,发现操作等于交换两个点到虚点的xor距离,而距离和边权一一对应,所以二者等价
设操作后新建边的权为w,则满足(a1,a2,...,an)=(b1 xor w,b2 xor w,...,bn xor w),当n为奇数时w取a1 xor a2... xor an xor b1 ... xor bn即可,这是必要条件
C:当和%p=0显然无解,否则考虑把众数x乘逆元变为1,则有解的充要条件为 1的个数<=(p-1)+Σp-大于1的数
如果1比较多则可以 (p-1)个1 a (p-a)个1 b (p-b)个1...来构造,超了显然无解,没超就不断把众数提出来,若可以加就加否则加其他的数
若众数始终不变就同上,若变了可以发现一个非众数至少可以消掉一个众数,等于问一个序列每次把两个数-1是否有解,因为众数改变了所以最大=次大,显然有解
考虑算无解的方案,先去掉%p=0的,再设f[i,j]表示选了i个>1的Σp-a为j,由于无解所以1一定大于n/2即众数唯一,所以方案乘n即可
D:先求lis,若长2k则把f<=k的和>k的分成两组,否则为2k+1,由于不能在内部分,所以一定有一个非2k+1里面的被选,设其为x,则有解的充要条件为x在一条>=k+1链里
必要性显然,若没有则全在内部,分不出来
充分性考虑构造,把x所在的一段k+1上升序列拉出来,把f不在其中的和fi=fx且i!=x的丢到一起,剩下的丢到另一组,前面的由于x不影响2k+1链,所以去掉的只有k层剩下k+1,后面的有x所在k+1链且至多k+1层,所以都为k+1
E:把S变为数组a,满足相邻绝对值=1且ABC对应%3=012,发现只要确定a1后面唯一确定,同时若S->T则反过来操作a与S互相对应,所以只需要考虑所有a1即可
每次a->a±2,显然操作次数为\(1/2\sum |a_i-b_i|\)(固定住a=b的点中间往上/下靠),用桶存然后枚举a1-k做到O(n)
CF1495F. Squares
求答案显然等于求2n对点之间的而距离,把询问离线按y排序,维护i到当前点的最短路
注意图很特殊,没有相交的边,因此往右扫时先新增链边,接着某个点可能会跨过增加的边,因为边不相交所以可以按新增边u->v划分成两部分,路径显然要经过u,所以用边替换掉u->当前点最短路即可
用线段树维护区间加单点查,一个点加多条边就从后往前加,不断把新的最短路的范围往前扩
CF1495E. Qingshan and Daniel
首先可以知道剩下0还是1,然后考虑多的那边每个元素剩下多少
发现其被减的次数等于以其结尾的最大子段和,环的话复制一遍扫用单调队列维护
如果最大子段和是负的则其不会被减,否则整段的01会互相抵消,差就是减当前元素的次数,一开始要调一下使得能交替操作
题解貌似是直接扫,因为与操作顺序无关
CF1500C. Matrix Sorting
考虑两个最终序列的位置,发现可以变为两个列数组满足A的最后元素在B的所有元素之后,直接考虑相邻的即可有O(n)对限制
然后倒着贪心选,每次把没有限制的列全选上,总复杂度为O(n^2)
597的做法:从后往前做,每次把有序的划分集合,与划分顺序无关,维护一下每个元素的最长结尾上升子串即可O(n^2)
6995. 2021.03.06【2021省赛模拟】组合(zh)
同 之前学军比赛 和 dyp的题 ,长链剖分维护上面部分的情况,每次先把轻儿子的次数加进去(走重链)走重儿子,然后把和轻儿子重链等长的重儿子重链替换走轻儿子,出子树时把轻儿子次数撤掉
加/替换只会在轻边操作,所以是O(n)
CF1494F. Delete The Edges
发现转换后剩下的一定是个菊花,否则若连续走两条不同的边,则在走偶数次时一定会剩下一条边同时奇数时消不掉
那么把菊花去掉剩下的是个欧拉路,枚举终点,发现相连的奇点最多剩一个(否则个数>2或者非路径终点),枚举剩哪个判断跑欧拉路即可,O(m(n+m))
判断是度数条件+剩余每条未加的边都能到终点
gym101612D. Dividing Marbles
把给出的数按1分成两个数,类似辗转相除,把大数不断/2(奇数就先-1)来接近小数然后做差,如果相等了就不断-1/2
先除成奇数,特判一开始/3的情况,正确性未知见https://blog.csdn.net/nike0good/article/details/78536799
gym101480G. Greenhouse Growth
差分,发现A操作等于每段正的头-1前一段负的头+1,B类似,则一个数可能被A,B,AB操作,分三种记一下丢桶里维护,桶里面记录下每次操作的时间,只考虑最新的操作,a的变化就记下属于哪种类型,然后减掉(当前的值-上次更新时的值)
顺序枚举删掉当前桶里的,每次一定是丢到后面的桶里,用链表实现即可O(n)
注意细节,比如删的时候要先把删的集合扫几遍来确定删完的链表,然后再把pre和next修改,还有1和n的边界情况
gym100531E. Expression
屎题
建个自动机然后dp,设f[i,j]表示匹配i位到匹配串的j的最小长度,把i滚动,维护0->1和|T|-1->|T|时的位置,然后分三段还原
具体实现可以把奇怪的情况先判掉(多个星号,星号前面非字母),然后(连|,相邻|相连,|前一个字母连),(连星号,星号回连括号(可以全跳)
这种屑题跑最快有鬼用啊kora
gym101471L. Visual Python++
从右往左从下往上,每个左上角贪心匹配y不小于自己且最小的右下角,因为该点是当前x最大的,其余未匹配的点一定会穿过当前点往下的线段,所以必选y最小的
然后排序判断矩形相交,注意边界以及矩形可以退化为线段
gym100851D. Distance on Triangulation
想优化建图发现布星,然后直接分治即可,分治的总数每次减1/3
证明:设减不到1/3,则对于任意一条边都存在一边<1/3另一边>2/3,那么找一个点然后找其两条不能在往内卡的边,接着从一条边的另一个端点继续找往里卡
由于减不到1/3所以必然存在>=4条边,则可以在中间连至少一条边,由于前提条件有一侧<1/3,相比于该侧原来的边来说还可以往里卡,矛盾
CF1491H. Yuezheng Ling and Dynamic Tree
分块,维护f[i]表示i在块中最小的祖先,简单维护,查询类似树剖lca
因为复杂度写错了所以应该不用卡常
CF1491F. Magnets
先顺序询问i和i+1~n直到某个结果非0,则这个一定非-,用其询问后面的可以得到结果(可以询问i+2~n然后反推i-1)
然后前面最多存在一个S=N的,二分找即可,上界设到边界外这样可以判掉不存在的情况
CF1491G. Switch and Flip
假设对把一个序列12345依次和第一个交换,可以得到-5-1234,如果能原地翻转就解决了
但是并不能,所以考虑把前面的移到其他序列里,然后直接交换还原
把两个序列ab提出来,交换首然后用一个的首依次换另一个的其余部分,最后再把两个的首换回来,操作|a|+|b|次
然后会剩下一个序列12345,那么依次换得到-4-1235,然后-4-5231,-1-5234,51234这样还原,多了一次操作
注意可能剩下长2的序列,所以如果不止一个环就用其他元素依次换,由于n>=3所以没有只有一个2环的情况
牛客练习赛77F 小G的排列
推一下容斥系数:任意组合后最终长>m的链系数和=0,<=m和=1
给两边+1,\(\frac{1}{1-F}=\frac{1-x^{m+1}}{1-x}\),得\(F=1-\frac{1-x}{1-x^{m+1}}\)
dp,设f[i,j]表示放了i段总长j,随便写有n^3
发现每次转移新增的段长为k(m+1)和k(m+1)+1,所以把j按%(m+1)分类用桶维护转移就O(n^2)了,注意F[1]=1所以要减掉
6653. 【2020.05.27省选模拟】树
也不是dp
记sumi表示i的出现次数,贪心匹配一定是fa选小的,w选大的,这样不会冲突
不考虑构造距离的话存在sum[i-1]+2>i(枚举fax,满足fax<min(x),两个+1一个是初始为2,一个是当前的),即sum[i-1]>=i-1
如果要构造距离k,则等于选若干特殊点,满足特殊点从后往前连边
那么限制的下界会变为i,因为
2 3 4 5 6 7 8 9 10
1 1 1 2 2 2 3 3 3
有可能选了2和8,那么第一个3会向前一位匹配到7(选了一个<i的和一个>sum[i-1]的)
考虑什么时候会有sum[i-1]>=i-1,设sum[i-1]=i-1,考虑限制
2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 7 7
发现此时若7不选,则一定会出现上面的情况,而7刚好卡界所以无解
因此sum[i-1]=i-1时i一定选,等于当i选时sum可以等于i-1
所以若i选则sum[i-1]>=i-1且i存在,否则sum[i-1]>=i
那么两个指针维护一下,如果越过了就每多选一个移两步
6652. 【2020.05.27省选模拟】序列
并不是dp
nm^2做法:考虑每个序列中每个数的移动方向,发现对于任意两种数,其在两个序列的关系为ab,ab,则两个b的移动方向相同;若为ab,ba,则后面的b和a移动方向相反,并查集连边最后构造
正解:设某个序列最后的数为a,将其移到结果序列开头(末尾镜像,*2即可),若其在其他序列的非末尾出现,则其后面的都要丢到末尾,丢到末尾的又会把一些丢到开头,一直这样操作下去可以把序列分成若干块,每块都可以翻转,所以ans=2^k(特判最后长1的)
构造就从内往外贪心即可
具体实现可以先把一种序列构出来之后再依次判断是否合法,这样只用记每个数是否加过然后加就行了
uoj#606. 【UER #9】面试
先询问(0,0,0)得到s=a+b+c,若s<=n则(0,n,0),(0,0,n),若s>=2n则(n,0,n),(n,n,0),其余n<s<2n
否则设2t=(n,s-n,0)=(n-a+c)+|n-a-c|,若a+c<=n则t=n-a,否则t=c,发现任何情况下t>=c
若s-t>n则询问(n,s-t-n,t)=2n+2t-2(a+c)得到a+c
否则询问(s-t,0,t)=(t+b-c)+|b+c-t|,注意t=c或n-a,两种情况下b+c-t>=0,所以得到2b
有了a+c后根据和n的关系就可以解出abc了
uoj#605. 【UER #9】知识网络
新建K个点,i->ai长0,ai->i长1,从某种颜色求最短路dis
发现如果能从x直接走最短路dag走到则dis-1,否则dis不变,因此求出dag后bitset拓扑求前驱即可
注意会卡空间,所以要多做几次+手写bitset
uoj#604. 【UER #9】赶路
把起点设为O终点放在x正半轴上,若极角排序后相邻<180则直接转,否则先转完第一象限的,然后在停止位置处往y<0的点走,走到连终点和y轴夹角最小的两个(根据叉积判走哪个),然后转圈

更简单的做法:从1开始随机一个点x,将剩下的分成两部分,然后递归做1->x和x->n
gym100543L. Outer space invaders
发现问题等价于有若干由y>=di,x∈[ai,bi]围成的向上无限矩形,在里面放一些点(bi,di)代价为di,使得每个矩形内部都有点
显然当前d最大的一定会被放,且放完之后由于d最大所以任何[a,b]跨过该点的矩形都会被消掉
把b排序,设f[i,j]表示ith-b,jth-b已放,放完中间的代价,转移枚举maxd的[a,b]中的点分裂,O(n^3)
gym102482D. Gem Island
想kthmin-max容斥,然后发现有个大组合数
简单推导发现每种最终情况的概率是一样的,所以直接f[i,j]表示答案/概率,g[i,j]表示方案/概率,n^3转移
(鬼知道double怎么过的
gym101242K. String Theory
发现问题等价于找一个k种括号的序列,满足k->k-1且存在1,i的编号为i,按顺序写下后合并相邻的可以变为序列a
设枚举K,设f[i,j,k,l=0/1]表示ai剩j,当前放到k,是否已放k-1的0/1状态
当k=1时l=1,k>1时只有l=1时才能放k变为k-1,否则只能放k+1,时间O(n^4),注意特判K=1
gym101221I. Sensor Network
枚举最远点,其余的合法点被限制在两个扇形中间,分成了两部分在上面找最大团
补图是二分图,直接O(n^4.5)过
gym101239H. Qanat
设x[i]表示第i个井的位置,x[0]=0,x[n+1]=w
设xi-1和xi+1已确定,经过疯狂化式子得到:\(\large x_i=A(x_{i-1}+x_{i+1})\),其中\(\large A=-\frac{k^2-1}{2}\),k=h/w
随便解
gym101239E. Evolution in Parallel
一些性质:
①祖先关系可以传递,若a不是b的祖先则a的后代也不是b的祖先
②合法方案中,任意三个必存在一对祖先后代关系
维护两条链,每次能加则加,否则找到两条链最后一段不是新加的祖先的,然后用新的点和最前的各一个点操作,因为②所以两个点间一定有边,不断往下展开,这样应该是O(n^3log)
考虑优化,每次两边都能加时记下另一边的边,然后反着展开
显然不好写,考虑硬点两边都加时加到左边,这样展开就只有一侧,记下最后一条右x->左y的边即可,若都不能加就判断左边y上一个点,显然这个点和x之间没有关系,若新的点也与该点无关系则无解,否则加进去
时间O(n|S|)
gym102511K. Traffic Blights
考虑x%a=b,x%c=d的解,若(a,c)=1则一定有解,否则要满足b=d (%(a,c))
设X=64*81*25*49,把%Li变为%[Li,X],这样变成了一条%X=a和若干%Xpi=a
后面的gcd等于X,所以枚举t%X等于多少,后面就一定有解,直接相乘
但这样X太大了,考虑把X变为8*9*5*7,发现多了8X,9X,7X,5X(2X,4X->8X,6X超了),仍然gcd=X,做法同上
gym100269C. Correcting Curiosity
设f[i,j]表示用[i,j]替换[i,n]的次数,i=n->1枚举同时在sam上跑,维护right集合二分下一个替换位置
求出次数后用len+(m-n)/f算出替换串的长度,再做一遍hash判断
CF1486F. Pairs of Paths
相交一共有两种情况:①lca不同,小的lca在大的链上且无交 ②lca相同,链无交
第一种从下往上dfs,线段树一个log维护,标记打在lca和lca下面两个点上询问链和,转化为区间改单点查
第二种枚举lca容斥计算
gym101190C. Cactus Construction
找一棵dfs树,若没有返祖边就把子树合完后根设为3其余为1,新的根设为2连2-3再改为3
有返祖边就把下端设为4,合并顺序先合返祖边到t的,然后合新增下端的,最后合剩下的
CF1307G. Cow and Exercise
先看了官方题解&洛谷题解,发现最后的式子是一样的但是理解方式不同(与下面的)所以感觉很奇怪
参考:https://www.cnblogs.com/Grice/p/13978598.html
先列出最终问题的线性规划,x表示增量d表示dis,二分ans
\(min(\sum x_{ij})\)
\(\left\{\begin{matrix} d_j \leq d_i+w_{ij}+x_{ij} \\ d_T-d_S \geq ans\\ x_{ij}\geq0,d无限制 \end{matrix}\right.\)
对偶可得
\(max(\sum f_{ij}w_{ij}+F*ans)\)
\(\left\{\begin{matrix} -f_{ij}\leq 1\\ \sum f_{ix}-\sum f_{xi}=0\ \ \\ \sum f_{ix}-\sum f_{xi}-F=0\ \ (x=S) \\ \sum f_{ix}-\sum f_{xi}+F=0\ \ (x=T) \\ f_{ij}\leq 0,F\geq 0 \end{matrix}\right.\)
把f取反,发现是个循环费用流,连i->j流量1费用-wij,连T->S流量inf费用ans
先去掉T->S跑,然后因为循环所以流量全部通过T->S流回,设去掉后跑F(非上面的)流量的代价Cost,则实际代价为F*ans+Cost
设询问X,因为原问题<=X所以max(...)<=X即对于任何流量都成立,即F*ans+Cost<=X,有ans<=min((X-Cost)/F),求出最大流然后判断即可
判断只用判整点,因为函数图像长这样,因此可以对整点三分
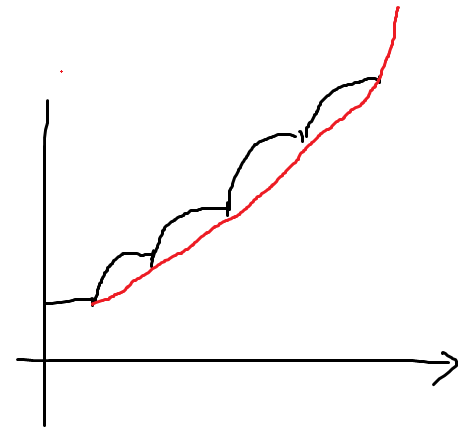
关于两种做法的差别:题解的最后做法的ans与中间过程的x有关,因此(也许)不能随便改;而上面做法的ans只与答案计算有关,因此可以直接设为上界
arc113E - Rvom and Rsrev
当a个数为偶数时可以全删,就尽量把a移到最右边,如果最右边没有就全删
当a为奇数时最后有a就同上,否则若最后一个a在后3位就全删(用删2b来换不优),否则一定要删2b换a
然后把a聚起来,先把头的一长段往后移(优先并>=2的),然后用2b翻到末尾
中间判掉一些零散的情况可以简化讨论
6991. 2021.2.20【2021省赛模拟】仲夏夜跑步
小孩召开法(并不
设f[i]表示长i的a1>a2<a3>a4...排列个数,最后只需要在最前面加上1即可
直接枚举1的位置,这样需要讨论前面长是否为奇
发现把符号反过来变为a1<a2>a3<a4...和原来的一一对应(a->n-a),所以把两条用同一个f的式子相加得
各种证明:
\(sinx'=cosx\),\(cosx'=-sinx\),设Δ然后展开
\(\large sinx=\frac{x^1}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}...\)
\(\large cosx=\frac{x^0}{0!}-\frac{x^2}{2!}+\frac{x^4}{4!}...\)
泰勒展开代入x0=0,sin(x0)=0,cos(x0)=1
\(tan'(x)=\frac{1}{cos^2(x)}\):\(tan'(x)=(\frac{sinx}{cosx})'=\frac{cos^2x+sin^2x}{cos^2x}=\frac{1}{cos^2x}\)
\(arctan'(x)=\frac{1}{x^2+1}\):
\(设y=arctan(x),x=tan(y)\)
\(y'=\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}=\frac{1}{tan'(y)}=cos^2(y)=\frac{1}{x^2+1}\)
\(x^2=\frac{sin^2}{cos^2}=\frac{1-cos^2}{cos^2},(x^2+1)cos^2=1\)
最后的变化:
\(sin2x=2sinxcosx,cos2x=2cos^2x-1,\frac{sinxcosx}{cos^2x}=tanx=\frac{sin2x}{cos2x+1}\)
\(tan(\frac{x+\pi/2}{2})=\frac{sin(x+\pi/2)}{cos(x+\pi/2)+1}=\frac{cosx}{1-sinx}\)
6989. 2021.2.20【2021省赛模拟】皇城 pk
发现\(f(n,k)=(s+1)!\binom{s+k}{s+1}\),sb(我&题解)的做法是把下降幂用斯特林转为普通幂,然后变为自然数幂和,接着插值解决
其实要求奇数位的等于乘上(-1)^i,然后相减/2即可得到,所以
\(\large (s+1)!\sum_{i=L}^R \binom{s+k}{s+1}(-1)^{s+k}=[x^{s+1}]-(s+1)!\frac{(-x-1)^{s+R+1}-(-x-1)^{s+L}}{1-(-x)}*\frac{1}{2}\)
上面的递推,直接O(s)求解
6988. 2021.2.19【2021省赛模拟】甲鱼漂泊
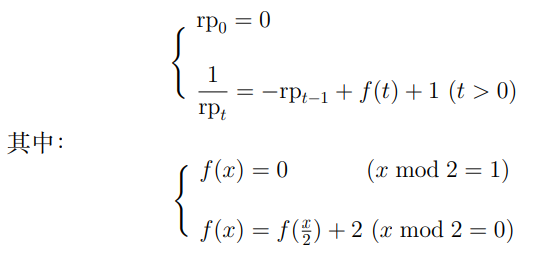
发现倒数操作等于分子分母交换,所以把分母写下来有
1 2 1 1 3 2 3 1 4 3 5 2 5 3 4 1
即每次复制一遍然后把相邻两个求和写在中间,辗转相除即可log解决
题解归纳证明
6987. 2021.2.19【2021省赛模拟】守望先锋
如果当前x往下k位的max确定了,则加上fa[x]可以贡献到长度k+1
所以可以直接求出f[i,j]表示i往下j的max,在每个点用堆即可维护修改
然后再维护一下每个点的答案,即找两条来自不同子树的链拼起来,一次操作后会改k个点每个点k所以O(nk^2log),也是用堆维护答案
CF1479E. School Clubs
停时,构造形如\(\sum f(a_i)\)的状态,记\(f(k)-f(k-1)=g(k)\)
把式子列出来:
\(\frac{1}{2}(\sum_i \frac{a_i}{n}(g(1)-g(a_i)))+\frac{1}{2}(\sum \sum \frac{a_i}{n}\frac{a_j}{n}(g(a_j+1)-g(a_i)))-\frac{1}{2}\sum \frac{a_i^2}{n^2}(g(a_i+1)-g(a_i))\)
(注意如果换到原来的组里的变化为0,所以最后要减掉)
化简得到与g(ai+1)和g(ai)有关的方程,解得\(g(k)=\prod_{i=0}^{k-1}\frac{2n-i}{n-i}\)
把a排序后求出f(ai)和f(n),前缀和维护分数
arc112F - Die Siedler
只要有一个cj>=2j就可以操作,直到所有都<2j为止
设\(f(c)=\sum 2^{i-1}(i-1)!c_j\),则操作后f不变,进一步发现除全0和全2j-1外f和c在<2j下一一对应(当成一个数)
所以初始的f每次可以加上f(s)再模\(N=2^nn!-1\),即每次加上\(\Delta f=gcd(N,f(si))\)
即要求所有\(f(c)=f(c') (mod\; \Delta f)\),把n=1~16都打出来发现N由一个不超1300000的数乘上一个大质数得到,所以gcd小dp,gcd大暴力
arc112E - Cigar Box
最后剩下未操作的一定是一个区间,枚举剩下的然后正着做
设固定表示最后一次操作,每次找一个为固定的移到左右,或者将其固定到对应位置(当区间非空时一定唯一),注意到固定分左右两种情况,所以在外面乘上组合数,里面即可唯一确定
设f[i,j]表示操作i次剩下j个的方案,这样即可求出区间非空的情况
区间为空(即操作全部数)的情况考虑枚举第一个固定的数以及操作次数,然后变为子问题解决
CF1479D. Odd Mineral Resource
套路,每种颜色随机权值取异或,用主席树以颜色为时间轴+二分可以log^2(要卡常
如果按照从根往下建树+二分或者欧拉序+二分可以一个log
6981. 【2021.02.03冬令营模拟】在星河里
m为奇时重心唯一,设M为输入的m,m=M/2,p=M-m-1
枚举重心,考虑所有子树,设s为size
\(\large [x^M]\prod \sum_i \binom{i+s-1}{s-1}x^i - \sum_{i>=m+1} \binom{i+s-1}{s-1}x^i\)
$=\large \binom{n+m-1}{n-1} -[x^p]\sum \frac{1}{(1-x)^{n-s}} \sum_{i} \binom{i+m+s}{s-1}x^i $
$=\large \binom{n+m-1}{n-1} -[x^p]\sum \frac{1}{(1-x)^{n-s}} \sum_{i} \binom{i+m+s}{s-1}x^i $
\(=\large \binom{n+m-1}{n-1} - \sum \sum_{i} \binom{i+m+s}{s-1}\binom{p-i+n-s-1}{n-s-1}\)
右边的预处理s爆算可以O(nm),用组合意义把i放进去,加上i左边有至少m+1个空这一限制,枚举s-1个左边的有多少在第m+1个空左边:
\(\large =\sum_{i=0}^{s-1} \binom{i+m}{i}\binom{M+n-1-(i+m+1)}{n-1-i}\)
前缀和O(n)处理
当m为偶数时发现可能的重心为一条链,用sum-min点分解决,每次把顺序的数组下传+按顺序枚举min即可O(nlogn),注意计算子树内放m个用的是原size而不是块的size
6980. 【2021.02.03冬令营模拟】你的世界
考场做法:发现n<=2或m<=2一定是yes,具体可以通过斜操作移动1然后在边界消掉
然后暴力枚举[1,1],[1,2],[1,3]的横竖斜共7个状态,先往下推得[i,1~3],再往右推得[1~3,j],接着从[4,4]往右下推,时间O(T128nm)能过
正解:如果只有横竖操作,一个结论是有解的充要条件是任意2*2的格子1为偶数,所以一个2*2格子的值是四个斜线的和,发现等价于两对相对斜线和的异或关系,并查集连边,O(Tnm)
奇怪做法:判一下[i+1,j],[i+2,j],[i,j+1],[i,j+2],[i+1,j+3],[i+2,j+3],[i+3,j+1],[i+3,j+2]异或是否为0(?
6977. 【2021.02.02冬令营模拟】去南极
先dp设f[i]表示i的概率,可以写出与Σf[i]*i和Σf[i]*i^2有关的递推式,用矩乘+线段树维护
具体来说,维护[1次和,2次和,1],转移矩阵拆成两部分,把常数项([3,1],[3,2])单独拆开,变为求Π(Ai+Bi)的形式,B是常数部分
可以发现乘法分配律拆开后只有AAAAA和BAAAA两种情况(AB=B,BB=0),所以维护B加了几次即可
CF1476F. Lanterns
dp,设f[i]表示处理完前i个能完整覆盖的前缀,转移考虑i往左/右,往右如果f[i-1]覆盖了i就可以往后加,往左一是可以覆盖[i-ai,i-1],二是可以覆盖某个j满足f[j]+1>=i-a[i],这样中间的就被覆盖了,所以中间的全部往右,即f[i]=max(k+a[k]),k∈[j+1,i-1]
用二分+st表维护
CF1476G. Minimum Difference
带修莫队,把cnt相同的合并后只有√n个,直接找
注意维护相同cnt要用链表,不能带log
6976. 【2021.02.01冬令营模拟】拉拖机
容斥变为小于等于,每次把最小的行/列填数,这样填对其余的没有影响,所以可以填完后删掉,最后把每次的相乘
设有c行d列值q,则贡献为
\(\large\sum_x \sum_y \binom{c}{x}\binom{d}{y}(-1)^{x+y}(q-1)^{xm+yn-xy}q^{cm+dn-cd-xm-yn+xy}\)
提一下多余的再枚举x,后面的y用二项式反演+快速幂解决


 浙公网安备 33010602011771号
浙公网安备 33010602011771号