对比:逻辑回归&支持向量机&因子分解机
前言:
从去年的一月份报名马士兵教育人工智能系列课程已经4个月过去。学习过程中记了不少笔记,一直琢磨着待觉得差不多的时候将笔记稍作整理,建个博客。以费曼学习之法,加深记忆。刚好最近学习到了因子分解机器。顿挫之后决定以此作为第一篇博文论题之选。
14年毕业之后未再提笔学习,学习起步的过程非常的痛苦,今自觉渐入佳境。 回首之时,忆起学生时代学习的点点滴滴。文字作备忘,亦作查阅,亦作消遣。
当时决定学习人工智能的目标是今年6月份生日前夕找到工作。如今只剩下一个月时间,总结学过的模型,跑一跑代码,有时间再学习学习NLP更多的模型。就业方向:NLP和搜索推荐相关。
2021-05-10 与苏州昆山花桥新家小书房
- 逻辑回归LR
- SVM支持向量机
- FM因子分解机
- 异同优缺
一、 逻辑回归 LogisticRegression
背景:二分类任务
输入 :[ [X1,X2,...,Xn], [Y] ]
输出 : 0<y<1
机器学习学习的主线: 损失函数、求解方法 、改进优化
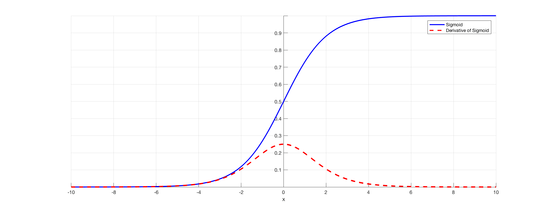
- 特征激活函数(sigmoid): f(x) = 1/(1+e^(-d))d = w0 + w1x1 +w2x2 +...+wnxn = W·X
- 值域在0~1之间,具有概率意义。对比MSE来说值域更符合概率意义。
- 图像:
![]()
- 比较软,数值变化非常平滑。也能找到一些函数值域在0~1之间,但都没有它好。
- 符合正态分布的规律。 (计划后面写一篇关于选择它作为逻辑回归激活函数的专题)
- 求解方法:
- KL距离: 通过激活函数后的值具备处于0~1之间,因此通过机器学习赋予它概率意义。这里我说这个概率意义是机器学习赋予它的:
- 我觉的这是机器学习最大的精髓之处,使处理之后的数值具备物理意义。它的概率意义的获得是自交叉熵比较概率分布之时开始获得,在梯度下降过程中逐渐成型,再模型优化过程中趋于成熟。(交叉熵后面也计划补个专题,单独介绍为什么选用KL距离作为优化目标)
- 梯度下降法(GD):随机初始化一个w,wi+1 = wi - λ(∂L/∂w)
- λ超参数,学习速率。需要人为调参,一般默认为0.002左右。
- KL距离: 通过激活函数后的值具备处于0~1之间,因此通过机器学习赋予它概率意义。这里我说这个概率意义是机器学习赋予它的:
- 改进优化
- 防止过拟合:理论上最后的w学习到是的KL最小,但是为了在测试集上获得最好的效果,通常会采取一些方法
- 提前终止学习。
- 加大训练集数据量。
- 人为选择特征
- 引入正则项 L1 或者 L2
- L1正则 ,特征选择,忽略一部分特征,让部分特征的权重为0
- L2正则 :力求把所有特征都用起来,同时能够加速梯度下降,将w的数量级约束在可控范围之内。
在机器学习中,加速学习过程是个很好的研究方向,在实际应用中,无论是由于项目场景要求训练周期短,或者为了防止过拟合,再或者因为当前机器算力限制,通常会采取一些方法简化学习过程,加快学习速度。
- 添加正则项,约束w的学习方位 KL + λL2 λ正则权重,决定了是训练集的数据对学习贡献大还是正则项对模型训练结果影响大。
- 特征优化: 归一化,优化学习路线。从反向过程来看:逻辑回归模型的参数优化一般采用了梯度下降法,如果不对特征进行归一化,可能会使得损失函数值得等高线呈椭球形,这样花费更多的迭代步数才能到达最优解。
- 防止过拟合:理论上最后的w学习到是的KL最小,但是为了在测试集上获得最好的效果,通常会采取一些方法
以上是基于LR原理的优化,但在实际应用中,LR的实际应用场景并不多,但作为一种更好模型发展起来的思想,还是很有必要进行深入的理解。为了解决实际场景出现的问题,同维度的优化显然已不能满足。因此,SVM支持向量机横空出世,并在相当一段时间中受到追捧。曾今的分类王者 ——支持向量机。
二、SVM(支持向量机)
曾经的分类王者。在今天的应用很少了。但学习AI不能不知道。
三、FM 因子分解机
论文原文:https://ieeexplore.ieee.org/document/5694074
背景:传统LR回归模型的训练需要花精力在特征的选择和特征的认为组合上。FM为这种问题提供了一种机器学习来解决的方法。就是因子分解。其实在我第一遍学习的时候我并没有接触到“因子分解机”这个说法,反而是看到这个说法后加深了我对FM模型的理解。从最简单例子来理解:
-
- 假设有两个特征:
X1(性别) X2(年龄在4~8岁之间) W12·X1x2 u1 0 1 u2 1 1 - d =w0 + w1x1 + w2x2 +w12x1x2 ==>这个式子很熟悉,这不就是高中解方程最常见的因式分解解方程吗形式吗?
- 因此d = (w1x1-b)(w2x2-c)的形式
- => w12 =w1·w2 ,w0 = b
- 因此w12可以用向量内积的形式来表示是,这样将原本组合特征和每个组合特征独立相关o(n2) =》之和有多少初始特征相关o(n),复杂度(线性的)降低的同时,满足了两两交叉组合特征的目的。
- 假设有两个特征:
- 特征激活函数
- 和LR的区别在于组合特征的权重
- 和LR的区别在于组合特征的权重
-
求解方法:
-
梯度下降法:运用数学技巧降低运算量复杂度。这里的学学习过程和LR相同,只不过公式寓所不同。
-
-
方法优化:
-
FM 在处理两两特征组合比较得心应手,但在处理更多特征组合时,目前机器的性能不能很好地发hi这个模型的效果。
- FFM:在业务场景成熟的公司,可以通过业务经理或者产品经理将特征进行fiel的分类,往往能达到更好的效果。
-
四。优缺
| 模型 | 逻辑回归 | SVM支持向量机 | FM因子分解机 |
| 优点 |
|
1. 分类超平面仅有支持向量决定,大大降低了噪声点,对模型训练效果的影响。
|
1.是对LR的缺点是一个很好补充。 2.在处理高稀散数据时效果很好 3.参数的学习过程是线性的,便于优化。 4.FM包含了许多最成功地协同过滤方法,包括有偏差的MF、SVD++、PITF和FPMC |
| 缺点 |
|
1.在处理特征稀散的场景效果比较差,这是因为分类仅由SV决定,儿特征空间往往时上亿维度,这意味着超平面也是上亿维度。 2.通过和技巧将高维度问题降维计算,存在不可解释性。维度越高,牺牲的性能越高。 3.对比LR来说,损失函数用于分类相比不具备概率意义。 4.SVM的密集参数化需要直接建模相互作用,通常在稀疏环境中无法进行。 5.对比LR,LR的梯度训练可以通过部分训练集数据来进行。SVM的支持向量理论上有所有数据所决定。 训练及数据都是耦合的,对计算机性能是极大的,所以,目前只在训练数据量不大的情况下使用。 |
暂时还没想到 |
没有免费的午餐定理
· 模型的优点往往是模型的缺点!业务场景+ABtest = 》最好的模型。
posted on 2021-05-13 09:35 life‘s_a_struggle 阅读(455) 评论(0) 收藏 举报


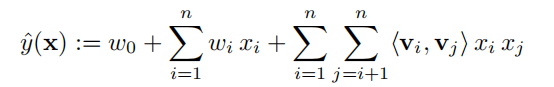
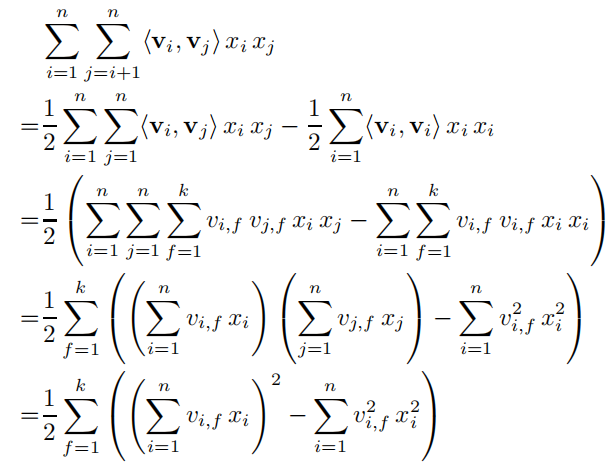
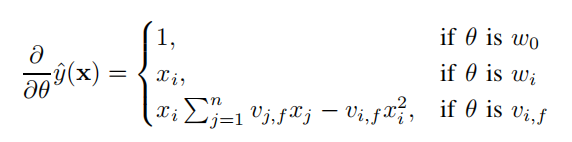

 浙公网安备 33010602011771号
浙公网安备 33010602011771号