会员
周边
新闻
博问
闪存
众包
赞助商
Chat2DB
所有博客
当前博客
我的博客
我的园子
账号设置
会员中心
简洁模式
...
退出登录
注册
登录
ghzhan
博客园
首页
新随笔
联系
订阅
管理
上一页
1
2
3
4
5
下一页
2023年8月26日
自动启动浏览器联网
摘要: 1,安装相应的python库 2,下载 edge 浏览器驱动 weddriver python 文件转成exe文件 Python 生成exe程序_python生成exe_minky糕的博客-CSDN博客 参考链接 编写python代码实现打开并登录网页、对网页进行点击、输入信息等操作_python
阅读全文
posted @ 2023-08-26 14:57 ghzphy
阅读(61)
评论(0)
推荐(0)
2023年5月19日
MATLAB 绘图
摘要: matlab直接保存图形而不显示图形_matlab直接保存图片不显示_faith默默的博客-CSDN博客 Matlab中图片保存的四种方法 - 技术蛀虫 - 博客园 (cnblogs.com) 暴力参数遍历 clear all tic N_L = 10; N_M = 10; N_N = 10; L1
阅读全文
posted @ 2023-05-19 19:41 ghzphy
阅读(77)
评论(0)
推荐(1)
2023年5月16日
拟合!!!!
摘要: 柳暗花明又一村!!!!!!!
阅读全文
posted @ 2023-05-16 19:39 ghzphy
阅读(60)
评论(0)
推荐(0)
2023年5月15日
Sentaurus学习
摘要: 快速入门 问题
阅读全文
posted @ 2023-05-15 21:30 ghzphy
阅读(94)
评论(0)
推荐(0)
2023年5月3日
常用物理常数
摘要: #### 物理常数 $$ q = 1.602176634\times 10^{-19}C\\ m_0 = 9.1093837015\times 10^{-31} kg\\ eV = 1.602176634\times 10^{-19}J\\ h = 6.62607015\times 10^{-34}
阅读全文
posted @ 2023-05-03 13:25 ghzphy
阅读(911)
评论(0)
推荐(0)
2023年4月29日
不光滑的态密度
摘要: 背景 在固体物理或相关物理教材可知,对于如下的非常经典的抛物线型色散关系 $$ H = \bm{k}^2 $$ 其对应的态密度色散关系为: 一维时, 与 $E^{-1/2}$ 成正比; 二维时,其是个常数; 三维时, 与 $E^{1/2}$ 成正比. 态密度公式 (参考下面该篇博士论文附录,先码住有
阅读全文
posted @ 2023-04-29 20:06 ghzphy
阅读(267)
评论(0)
推荐(0)
五一劳动节
摘要: 五一劳动节快乐!!!
阅读全文
posted @ 2023-04-29 19:47 ghzphy
阅读(21)
评论(0)
推荐(0)
2023年4月20日
最简单一维量子链求解实例
摘要: 写在前面: 5年前的笔记,再次做个备份. 假设器件长度为 $L$, 均匀分成 $N+1$ 份, 网格spacing 为 $a = L/(N+1)$. $$ H\varphi = -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\varphi = E
阅读全文
posted @ 2023-04-20 19:42 ghzphy
阅读(167)
评论(0)
推荐(0)
2023年4月18日
有限厚度 vs 周期性结构
摘要: 写在前面 本文将以二维 Weyl的哈密顿量为例 哈密顿量 $$ H(k_x,k_y)=v(k_x\sigma_x+k_y\sigma_y) + \frac{\Delta}{2}\sigma_z + E_f\sigma_0 $$ 这里, $v$ 是费米速度, $\Delta$ 是带隙, Weyl 锥关
阅读全文
posted @ 2023-04-18 17:10 ghzphy
阅读(145)
评论(0)
推荐(0)
边界条件
摘要:  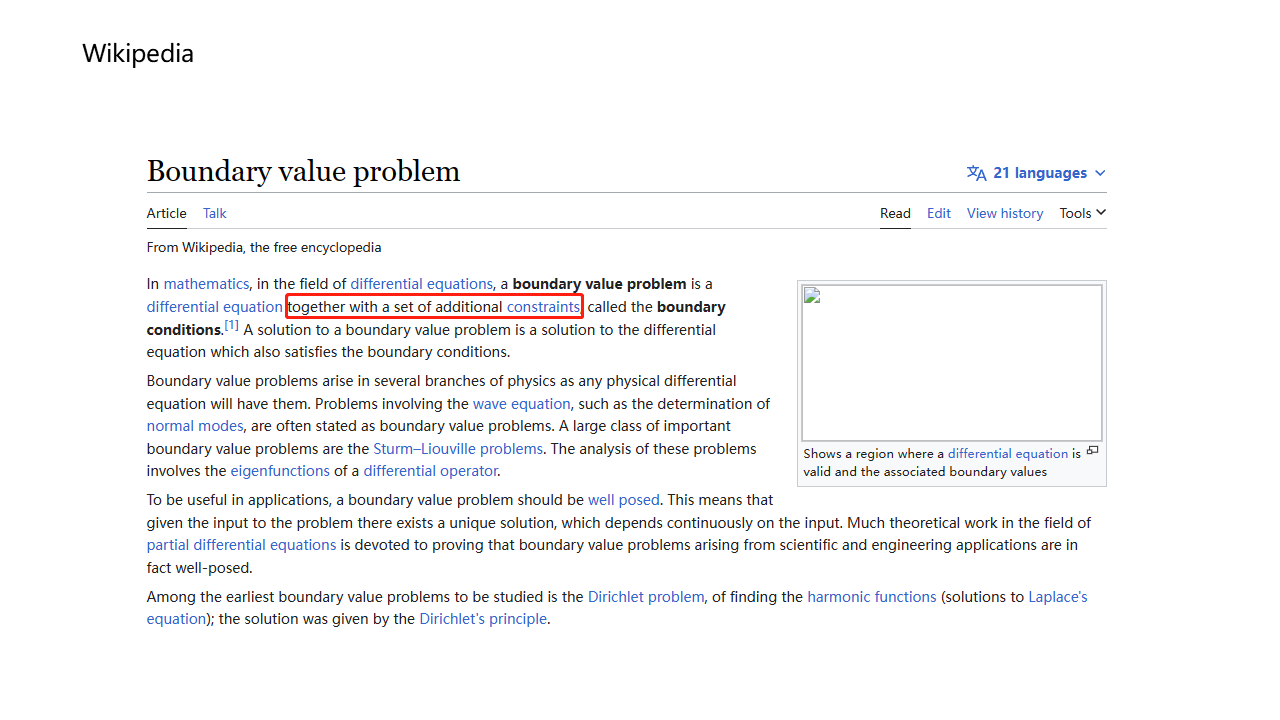 ![
阅读全文
posted @ 2023-04-18 13:39 ghzphy
阅读(145)
评论(0)
推荐(0)
上一页
1
2
3
4
5
下一页
公告