计算非中心 t 分布的累积分布函数——基于 LLM 的 Excel VBA 实现
微信群中发现有对数理统计中单样本 T 检验功效值计算的讨论,在 R 语言中 1-pt(qt(0.975,8),8,-1.571428571)+pt(-qt(0.975,8),8,-1.571428571) 得到 0.2834242。
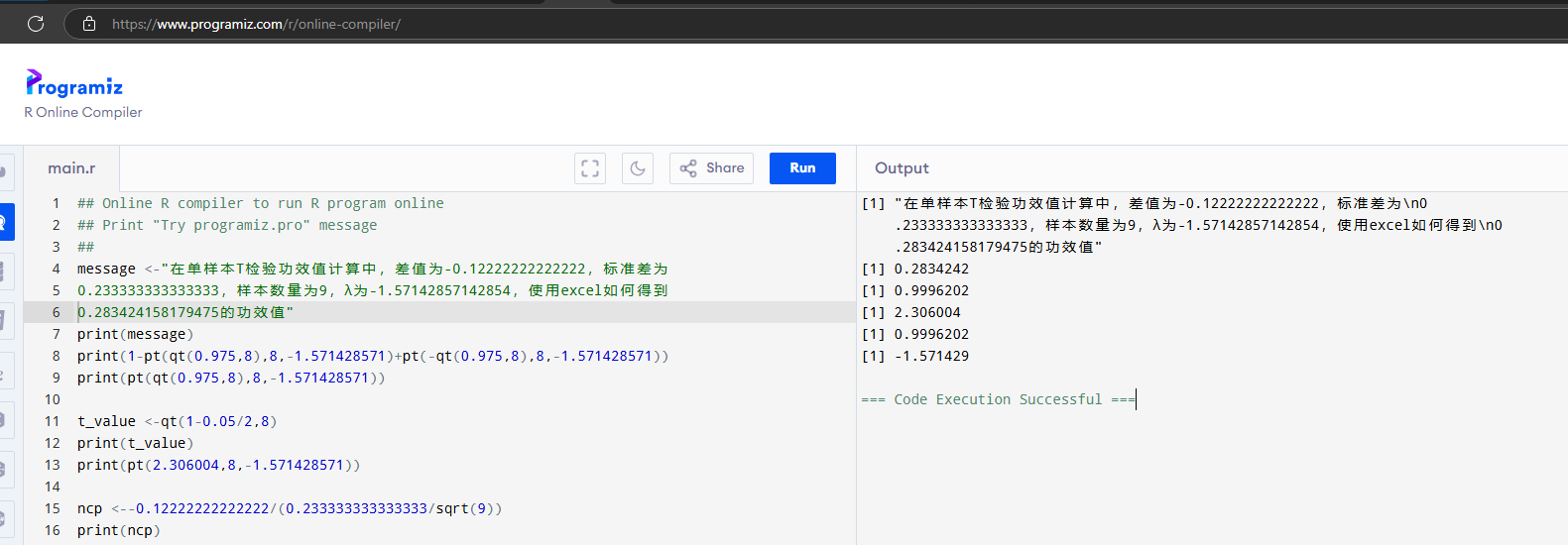
计算功效过程中用到了的非中心 t 分布,而 excel 原生没有对其支持,需要写自定义函数,
询问大模型及信息检索有如下的代码——
deepseek 等大模型的回答免不了幻觉。下图是 microsoft copilot中的回复





excel 中 T.DIST.NC 函数是不存在的。
使用多个大语言模型及传统搜索引擎,有如下结果
其一、
Function NonCentralTCDF(x As Double, df As Double, ncp As Double) As Double
' 基于AS 243算法实现非中心t分布的CDF
Dim eps As Double, iterMax As Integer
eps = 0.0000001: iterMax = 1000
Dim sum As Double, term As Double, lam2 As Double, pois As Double
Dim k As Integer, t As Double, beta As Double
Dim a As Double, b As Double
If df <= 0 Then
NonCentralTCDF = CVErr(xlErrValue)
Exit Function
End If
If x < 0 Then
NonCentralTCDF = 1 - NonCentralTCDF(-x, df, -ncp)
Exit Function
End If
t = x / Sqr(df + x * x)
lam2 = ncp * ncp
sum = 0
term = 0
k = 0
Do
a = 0.5 * lam2
' 计算泊松概率:exp(-a) * a^k / k!
If k = 0 Then
pois = Exp(-a)
Else
pois = pois * a / k
End If
beta = Application.BetaDist(t * t, k + 0.5, df / 2)
term = pois * beta
sum = sum + term
k = k + 1
Loop While (term > eps * sum) And (k <= iterMax)
sum = sum + Exp(-0.5 * lam2) * Application.Norm_S_Dist(-ncp, True)
NonCentralTCDF = sum
End Function
又一
Public Function NonCentralT_CDF(t As Double, df As Double, ncp As Double) As Double
Dim a As Double, b As Double
Dim x As Double
Dim sum As Double, term As Double
Dim k As Integer
Const MAX_ITER As Integer = 1000
Const EPS As Double = 0.000000000001
Dim lambda As Double
If df <= 0 Then
NonCentralT_CDF = CVErr(xlErrNum)
Exit Function
End If
lambda = ncp
a = df / 2
b = 0.5
x = df / (df + t * t)
' 初始项
term = Exp(-0.5 * lambda * lambda)
sum = term * IncompleteBeta(x, a, b)
' 迭代计算
k = 1
Do While k < MAX_ITER
term = term * (lambda * lambda / (2 * k))
Dim temp As Double
temp = term * IncompleteBeta(x, a + k, b)
sum = sum + temp
If temp < EPS * sum Then Exit Do
k = k + 1
Loop
If t >= 0 Then
NonCentralT_CDF = 1 - 0.5 * sum
Else
NonCentralT_CDF = 0.5 * sum
End If
End Function
' 不完全贝塔函数
Private Function IncompleteBeta(x As Double, a As Double, b As Double) As Double
Dim bt As Double
If x = 0 Or x = 1 Then
bt = 0
Else
bt = Exp(GammaLn(a + b) - GammaLn(a) - GammaLn(b) + a * Log(x) + b * Log(1 - x))
End If
If x < (a + 1) / (a + b + 2) Then
IncompleteBeta = bt * BetaCF(x, a, b) / a
Else
IncompleteBeta = 1 - bt * BetaCF(1 - x, b, a) / b
End If
End Function
' 贝塔函数的连分式展开
Private Function BetaCF(x As Double, a As Double, b As Double) As Double
Const MAX_ITER As Integer = 200
Const EPS As Double = 0.0000003
Dim m As Integer
Dim aa As Double
Dim c As Double
Dim d As Double
Dim h As Double
Dim del As Double
c = 1
d = 1 - (a + b) * x / (a + 1)
If Abs(d) < 1E-30 Then d = 1E-30
d = 1 / d
h = d
For m = 1 To MAX_ITER
Dim m2 As Integer
m2 = 2 * m
' 偶数步骤
aa = m * (b - m) * x / ((a + m2 - 1) * (a + m2))
d = 1 + aa * d
If Abs(d) < 1E-30 Then d = 1E-30
c = 1 + aa / c
If Abs(c) < 1E-30 Then c = 1E-30
d = 1 / d
h = h * d * c
' 奇数步骤
aa = -(a + m) * (a + b + m) * x / ((a + m2) * (a + m2 + 1))
d = 1 + aa * d
If Abs(d) < 1E-30 Then d = 1E-30
c = 1 + aa / c
If Abs(c) < 1E-30 Then c = 1E-30
d = 1 / d
del = d * c
h = h * del
If Abs(del - 1) < EPS Then Exit For
Next m
BetaCF = h
End Function
' 计算伽马函数的对数
Private Function GammaLn(xx As Double) As Double
Dim cof As Variant
cof = Array(76.1800917294715, -86.5053203294168, _
24.0140982408309, -1.23173957245015, _
1.20865097386618E-03, -5.395239384953E-06)
Dim x As Double, y As Double, tmp As Double, ser As Double
Dim j As Integer
x = xx - 1
y = x
tmp = x + 5.5
tmp = tmp - (x + 0.5) * Log(tmp)
ser = 1.00000000019001
For j = 0 To UBound(cof)
x = x + 1
ser = ser + cof(j) / x
Next j
GammaLn = -tmp + Log(2.506628274631 * ser)
End Function
其二、
Function NonCentralTCDF2(t As Double, df As Double, ncp As Double, _
Optional maxIterations As Long = 1000, Optional precision As Double = 0.000000000001) As Double
'================================================================================
' 函数名称:NonCentralTCDF2
' 功能描述:计算非中心t分布的累积分布函数(Cumulative Distribution Function)
'--------------------------------------------------------------------------------
' 参数说明:
' t : 分位数值(可正可负)
' df : 自由度(必须为正整数)
' ncp : 非中心参数(表示分布偏移量)
' maxIterations : 最大迭代次数(默认1000次)
' precision : 收敛精度(默认1e-12)
'--------------------------------------------------------------------------------
' 返回值:
' 返回概率值 P(T ≤ t),其中T服从非中心t分布
'--------------------------------------------------------------------------------
' 算法原理:
' 基于Lentz算法优化的级数展开法,核心公式:
' P(T ≤ t) = Σ [e^(-λ/2)*(λ/2)^k / k!] * I_r(k+0.5, df/2) + 修正项
' 其中:
' λ = ncp2/2
' r = t2/(t2 + df)
' I_x(a,b)为不完全Beta函数
'================================================================================
' ============== 参数预处理 ==============
' 处理自由度无效的情况
If df <= 0 Or df <> Int(df) Then
NonCentralTCDF2 = CVErr(xlErrValue)
Exit Function
End If
' 处理t为负的情况(利用非中心t分布的对称性)
If t < 0 Then
' 对称公式:P(T ≤ t | ncp) = 1 - P(T ≤ -t | -ncp)
NonCentralTCDF2 = 1 - NonCentralTCDF2(-t, df, -ncp, maxIterations, precision)
Exit Function
End If
' ============== 计算准备 ==============
Dim lambda As Double ' 泊松分布参数λ = ncp2/2
Dim r As Double ' Beta分布参数r = t2/(t2 + df)
Dim iterCount As Long ' 实际迭代次数计数器
Dim sumP As Double ' 累计概率和
Dim remainP As Double ' 剩余未计算概率
Dim term As Double ' 当前项的计算值
lambda = ncp ^ 2 / 2
r = t ^ 2 / (t ^ 2 + df)
sumP = 0
remainP = 1 ' 初始总概率为1
' ============== 级数展开计算 ==============
' 从泊松分布的均值点向两侧展开计算
Dim baseIndex As Long
baseIndex = Int(lambda) ' 泊松分布概率最大的位置
' 向下计算(baseIndex, baseIndex-1,...)
Dim downIndex As Long
downIndex = baseIndex
' 向上计算(baseIndex+1, baseIndex+2,...)
Dim upIndex As Long
upIndex = baseIndex + 1
With Application.WorksheetFunction
Do While iterCount < maxIterations And remainP > precision
' === 向下计算 ===
If downIndex >= 0 Then
' 计算泊松概率项
term = .Poisson_Dist(downIndex, lambda, False)
' Beta分布项计算
Dim beta1 As Double
beta1 = .Beta_Dist(r, downIndex + 0.5, df / 2, True)
' 修正项计算(包含Gamma函数比值)
Dim gammaRatio As Double
gammaRatio = Exp(.GammaLn(downIndex + 1) - .GammaLn(downIndex + 1.5))
Dim beta2 As Double
beta2 = .Beta_Dist(r, downIndex + 1, df / 2, True)
' 累加计算结果
sumP = sumP + term * (beta1 + (ncp / Sqr(2)) * gammaRatio * beta2)
remainP = remainP - term
downIndex = downIndex - 1
End If
' === 向上计算 ===
term = .Poisson_Dist(upIndex, lambda, False)
beta1 = .Beta_Dist(r, upIndex + 0.5, df / 2, True)
gammaRatio = Exp(.GammaLn(upIndex + 1) - .GammaLn(upIndex + 1.5))
beta2 = .Beta_Dist(r, upIndex + 1, df / 2, True)
sumP = sumP + term * (beta1 + (ncp / Sqr(2)) * gammaRatio * beta2)
remainP = remainP - term
upIndex = upIndex + 1
iterCount = iterCount + 1
Loop
End With
' ============== 最终结果修正 ==============
' 添加标准正态分布的尾部修正项
Dim normCorrection As Double
normCorrection = Application.WorksheetFunction.Norm_S_Dist(-ncp, True)
' 综合计算结果
NonCentralTCDF2 = sumP / 2 + normCorrection
' 确保结果在[0,1]范围内
If NonCentralTCDF2 < 0 Then NonCentralTCDF2 = 0
If NonCentralTCDF2 > 1 Then NonCentralTCDF2 = 1
End Function
其三、根据 Real Statistics Resource Pack for Excel 2010, 2013, 2016, 2019, 2021 or 365 for Windows 得到
Function NT_DIST(t As Double, df As Double, d As Double, cum As Boolean, _
Optional iter As Long = 1000, Optional prec As Double = 0.000000000001) As Double
' return non-central t pdf if cum = FALSE or distribution if cum = TRUE at t with df degrees of freedom and
' non-centrality parameter d; iter is the number of iterations and prec is the precision of the answer
If cum Then ' distribution function
If t >= 0 Then
NT_DIST = NT_DIST_CDF(t, df, d, iter, prec)
Else
NT_DIST = 1 - NT_DIST_CDF(-t, df, -d, iter, prec)
End If
Else ' pdf
If Abs(t) < 0.00000001 Or (Abs(t) < 0.0000001 And d <= 0.35) Then ' t is close enough to zero
NT_DIST = Exp(Application.WorksheetFunction.GammaLn((df + 1) / 2) - Application.WorksheetFunction.GammaLn(df / 2) - d ^ 2 / 2) / _
Application.WorksheetFunction.SqrtPi(df)
Else
NT_DIST = df * (NT_DIST(t * Sqr(1 + 2 / df), df + 2, d, True, iter, prec) - NT_DIST(t, df, d, True, iter, prec)) / t
End If
End If
End Function
Private Function NT_DIST_CDF(t As Double, df As Double, d As Double, iter As Long, prec As Double) As Double
' return non-central t cdf at t >= 0 with df degrees of freedom and non-centrality parameter d
' iter is the number of iterations and prec is the precision of the answer
Dim lambda As Double ' mean of Poisson distribution
lambda = d ^ 2 / 2
Dim i As Long
Dim df2 As Double ' df/2
df2 = df / 2
Dim dsq As Double ' d/sqrt(2)
dsq = d / Sqr(2)
Dim r As Double ' r
r = t ^ 2 / (t ^ 2 + df)
Dim p As Double ' p(i)
Dim ptot As Double ' total of the p(i)
ptot = 1#
Dim ctot As Double ' total of the cdf values
ctot = 0#
Dim hi As Long ' upper index
Dim low As Long ' lower index
low = Int(lambda)
hi = low + 1
With Application.WorksheetFunction
For i = 1 To iter
If low >= 0 Then
p = .Poisson_Dist(low, lambda, False)
ptot = ptot - p
ctot = ctot + p * .Beta_Dist(r, low + 0.5, df2, True) + _
dsq * p * Exp(.GammaLn(low + 1) - .GammaLn(low + 1.5)) * .Beta_Dist(r, low + 1#, df2, True)
low = low - 1
End If
p = .Poisson_Dist(hi, lambda, False)
ptot = ptot - p
ctot = ctot + p * .Beta_Dist(r, hi + 0.5, df2, True) + _
dsq * p * Exp(.GammaLn(hi + 1) - .GammaLn(hi + 1.5)) * .Beta_Dist(r, hi + 1#, df2, True)
If ptot < prec Then Exit For
hi = hi + 1
Next
NT_DIST_CDF = ctot / 2 + .Norm_S_Dist(-d, True)
End With
End Function
功效计算 1-NT_DIST(T.INV(1-alpha/2,df),df, ncp,true)+NT_DIST(-T.INV(1-alpha/2,df),df, ncp,true)
| 单元格 | 内容 | 公式或值 |
|---|---|---|
| A1 | ncp(非中心参数) | -1.57142857142854 |
| A2 | df(自由度) | 8 |
| A3 | α(显著性水平) | 0.05 |
| A4 | t_crit(临界 t 值) | =T.INV(1 - A3 / 2, A2) |
| A5 | Power(功效值) | =1 - NonCentralTCDF(A4, A2, A1) + NonCentralTCDF(-A4, A2, A1) |
 |
Python脚本核验
import scipy.stats as stats
def power_calculation():
# 参数设置
delta = -0.12222222222222 # 均值差
sigma = 0.233333333333333 # 标准差
n = 9 # 样本量
df = n - 1 # 自由度 = 8
alpha = 0.05 # 显著性水平
ncp = delta / (sigma / (n**0.5)) # 非中心参数λ
# 计算临界值(等效R的qt(0.975,8))
t_crit = stats.t.ppf(1 - alpha/2, df)
# 处理非中心参数符号问题(对称性转换)
def pt_noncentral(q, df, nc):
if nc < 0:
return 1 - stats.nct.cdf(-q, df, -nc)
else:
return stats.nct.cdf(q, df, nc)
# 计算右尾概率:P(T ≤ t_crit)
right_tail = pt_noncentral(t_crit, df, ncp)
# 计算左尾概率:P(T ≤ -t_crit)
left_tail = pt_noncentral(-t_crit, df, ncp)
# 总功效 = 1 - 右尾 + 左尾
power = 1 - right_tail + left_tail
return power
print(f"功效值: {power_calculation():.7f}") # 输出:0.2834242
以上,Real1Statistics 的宏函数更接近 R 或者 Python 的计算结果。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号