图

最短路径问题

可以使用 Dijkstra 算法。求一个节点到其他节点的最短路径。

Dijkstra 算法操作步骤：

1. 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为”起点s到该顶点的距离”[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。
2. 从U中选出”距离最短的顶点k”，并将顶点k加入到S中；同时，从U中移除顶点k。
3. 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。
4. 重复步骤(2)和(3)，直到遍历完所有顶点。

最短距离的维护是通过一个小顶堆来实现，每次找到距离最短的节点的时候删除堆顶元素，然后将新节点到其他节点的距离加入堆中。

第1步：初始化距离，其实指与D直接连接的点的距离。dis[c]代表D到C点的最短距离，因而初始dis[C]=3，dis[E]=4，dis[D]=0，其余为无穷大。设置集合S用来表示已经找到的最短路径。此时，S={D}。现在得到D到各点距离 {D(0)，C(3)，E（4），F（），G（），B（），A()}，其中 * 代表未知数也可以说是无穷大，括号里面的数值代表D点到该点的最短距离。

第2步：不考虑集合S中的值，因为dis[C]=3，是当中距离最短的，所以此时更新S，S={D,C}。接着我们看与C连接的点，分别有B，E，F，已经在集合S中的不看，dis[C-B]=10，因而dis[B]=dis[C]+10=13，dis[F]=dis[C]+dis[C-F]=9，dis[E]=dis[C]+dis[C-E]=3+5=8>4 (初始化时的dis[E]=4)不更新。此时{D(0)，C(3)，E（4），F（9），G（），B（13），A()}。

第3步：在第2步中，E点的值4最小，更新S={D，C，E}，此时看与E点直接连接的点，分别有F，G。dis[F]=dis[E]+dis[E-F]=4+2=6（比原来的值小，得到更新），dis[G]=dis[E]+dis[E-G]=4+8=12（更新）。此时 {D(0)，C(3)，E（4），F（6），G（12），B（13），A(*)}。

第4步：在第3步中，F点的值6最小，更新S={D，C，E，F}，此时看与F点直接连接的点，分别有B，A，G。dis[B]=dis[F]+dis[F-B]=6+7=13，dis[A]=dis[F]+dis[F-A]=6+16=22，dis[G]=dis[F]+dis[F-G]=6+9=15>12（不更新）。此时 {D(0)，C(3)，E（4），F（6），G（12），B（13），A(22)}.

第5步：在第4步中，G点的值12最小，更新S={D，C，E，F，G}，此时看与G点直接连接的点，只有A。dis[A]=dis[G]+dis[G-A]=12+14=26>22(不更新)。{D(0)，C(3)，E（4），F（6），G（12），B（13），A(22)}.

第6步：在第5步中，B点的值13最小，更新S={D，C，E，F，G，B}，此时看与B点直接连接的点，只有A。dis[A]=dis[B]+dis[B-A]=13+12=25>22(不更新)。{D(0)，C(3)，E（4），F（6），G（12），B（13），A(22)}.

第6步：最后只剩下A值，直接进入集合S={D，C，E，F，G，B，A}，此时所有的点都已经遍历结束，得到最终结果 {D(0)，C(3)，E（4），F（6），G（12），B（13），A(22)}.

多源 BFS 问题

例题：1162 地图分析

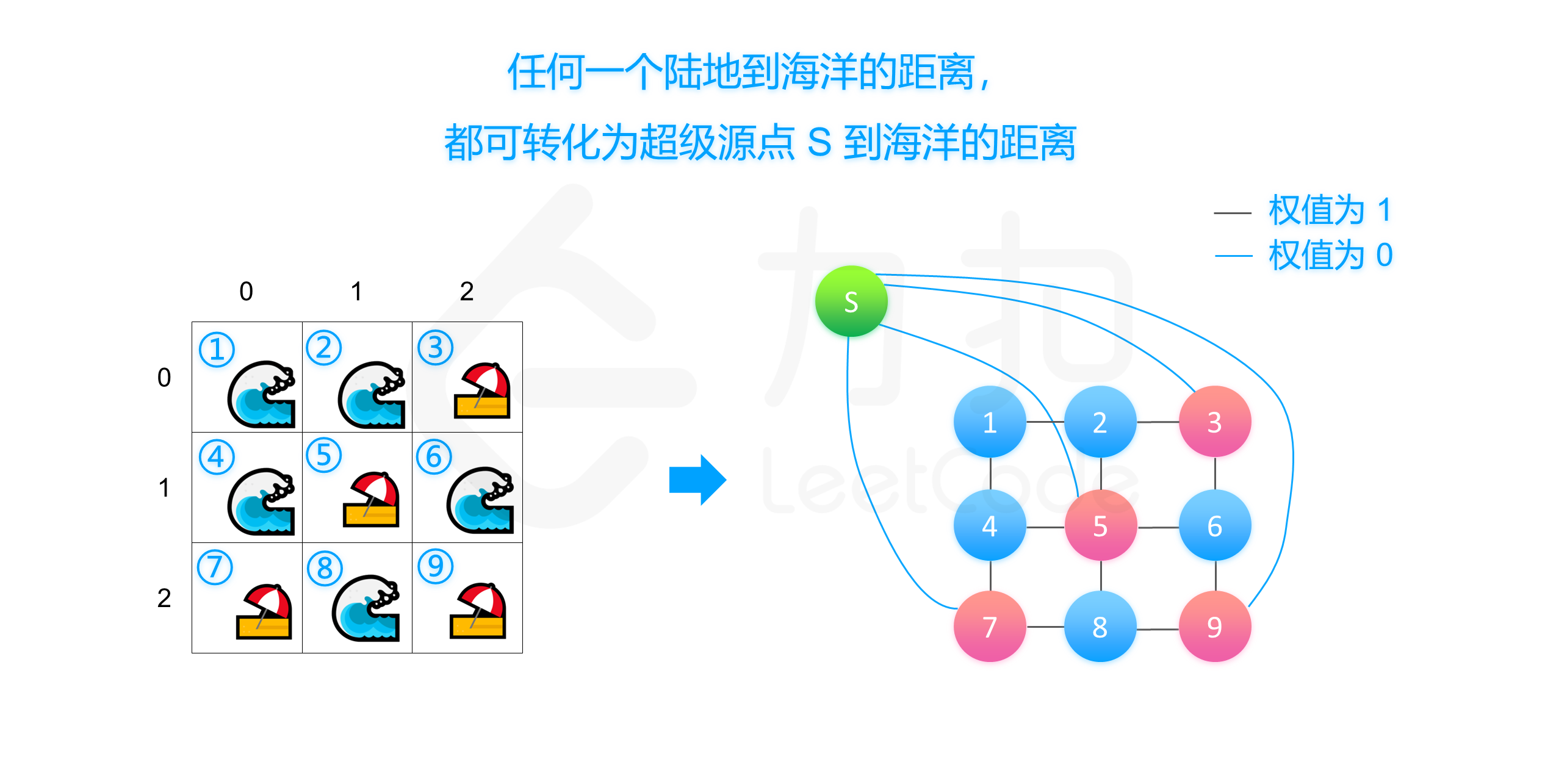
你现在手里有一份大小为 n x n 的 网格 grid，上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

示例 1：

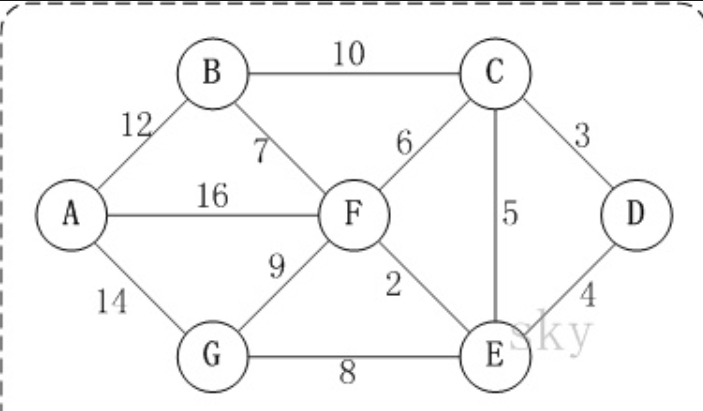
输入： grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释：
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

示例 2：

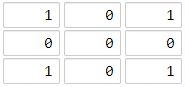
输入： grid = [[1,0,0],[0,0,0],[0,0,0]]
输出： 4
解释：
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

分析：

这道题首先第一个想法是使用递归+回溯的方法，但是要注意：递归法只适合查找路径类似于树状结构的题，这道题明显是一个图结构的题。递归 + 回溯本质上是一个 DFS + 回溯的搜索方。

如果本题使用递归方式来进行查找，可能会出现成递归环的情况，这样就死循环了。如图所示：

1
@1	@2	@3
@6	@5	@4

所以说这道题不能用递归的方式，只能考虑 BFS 来搜索了。如下是伪代码

for 每一个海洋节点 {
    初始化一个队列
    将自身加入队列中
    计算距离的计数器初始化 = 0
    for 队列不为空 {
        计算距离的计数器 + 1
        弹出队列一层的元素
        for 遍历这一层的元素 {
            如果是陆地节点：海洋节点到陆地的最短距离为计数器的值
            如果是海洋节点：将其推入队列中
        }
    }
    将所有海洋节点的计数器比较，取最大的值
}

经过分析，时间复杂度为：O(n ^ 4) ，遍历每一个海洋节点需要 O(n^2)，遍历每一个陆地节点需要 O(n ^ 2)。

多源 BFS 问题：

由上述 BFS 伪代码得知：这里本质上是要求海洋点到陆地点集合的最短路径，可以转换为海洋点到一个超级原点 S 的最短路径，点到点集的问题被转换为点到点的问题，然后就可以转换为 S 到海洋点集的最短路径。使用 Dijkstra 算法来求解一个点到其他节点的最短路径。