动态规划

动态规划

理论

01 背包

• 01 背包题目模板

for 遍历物品数组 {
    for 遍历背包容量（从大到小）{
        递推公式
    }
}

• 解释模板的含义：

dp[i] 是指在背包容量为 i 的时候，结果的值。这个模板是一个迭代的过程，从第一个物品开始，仅对于这个物品来说，对于每个背包容量有两种状态，要么加入背包，要么不加入背包。每次遍历物品都是将 dp 数据迭代一次。

背包容量从大到小遍历是为了保证每个物品只能被添加一次。

• 举一个例子：

背包最大重量为4。

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？

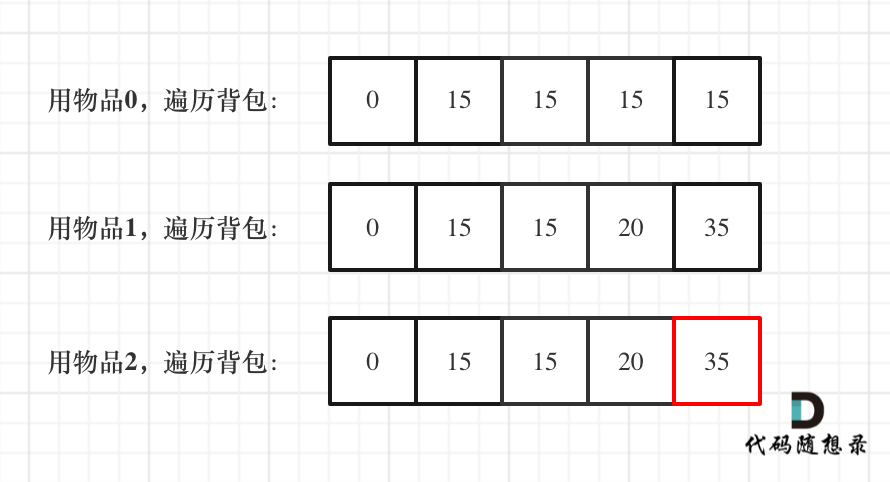
// weight[i] 物品 i 的重量
// value[i] 物品 i 的价值
for i := 0 ;i < len(weight) ; i++ {
    // 背包容量从大到小遍历
    for j:= bagWeight; j >= weight[i] ; j-- {
        // 递推公式
        dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
    }
}

完全背包

• 完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

• 完全背包模板：

  • 结果是一个排序，与序列有关

  • 结果是一个组合，与序列无关

// 结果是一个组合，与序列无关
for 遍历物品数据 {
    for 遍历背包容量（从小到大） {
        递推公式
    }
}

// 结果是一个排序，与序列有关
for 遍历背包容量（从小到大）{
    for 遍历物品数据 {
        递推公式
    }
}

• 举一个例子：

背包最大重量为4。

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

每件商品都有无限个！

问背包能背的物品最大价值是多少？

// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

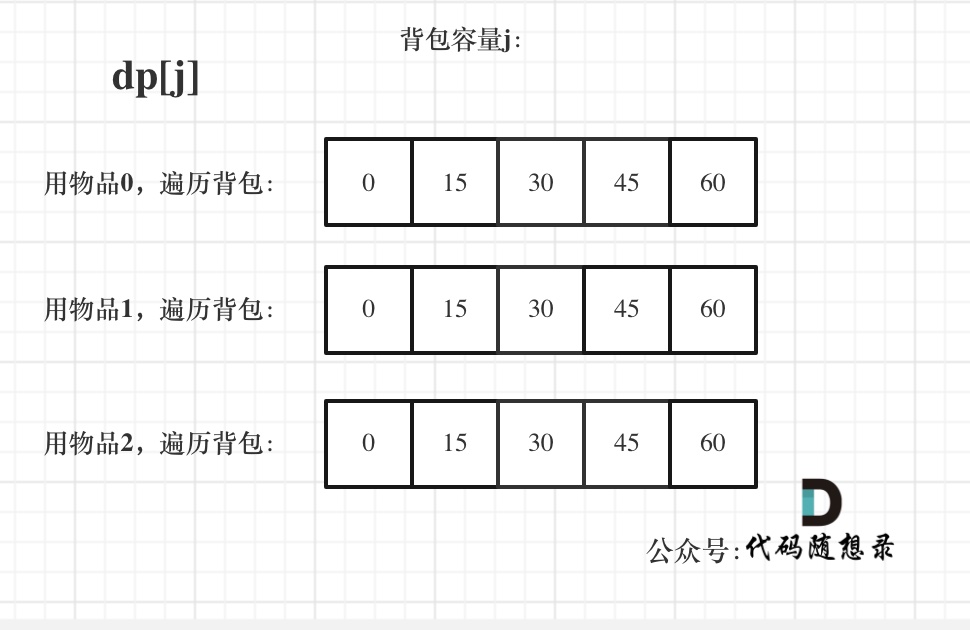
我们知道01背包内嵌的循环是从大到小遍历，为了保证每个物品仅被添加一次。而完全背包的物品是可以添加多次的，所以要从小到大去遍历。

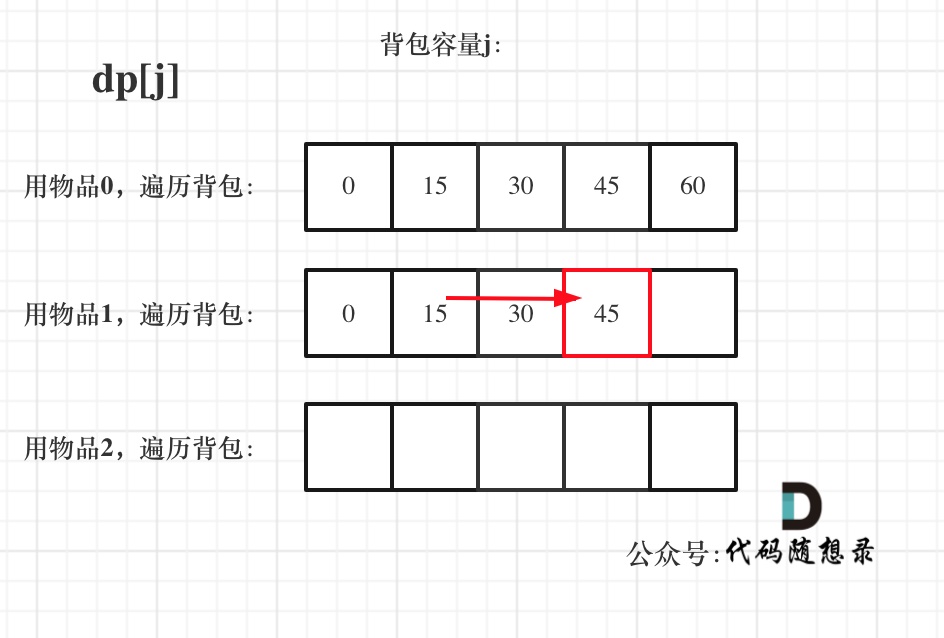
遍历物品在外层循环，遍历背包容量在内层循环，状态如图：

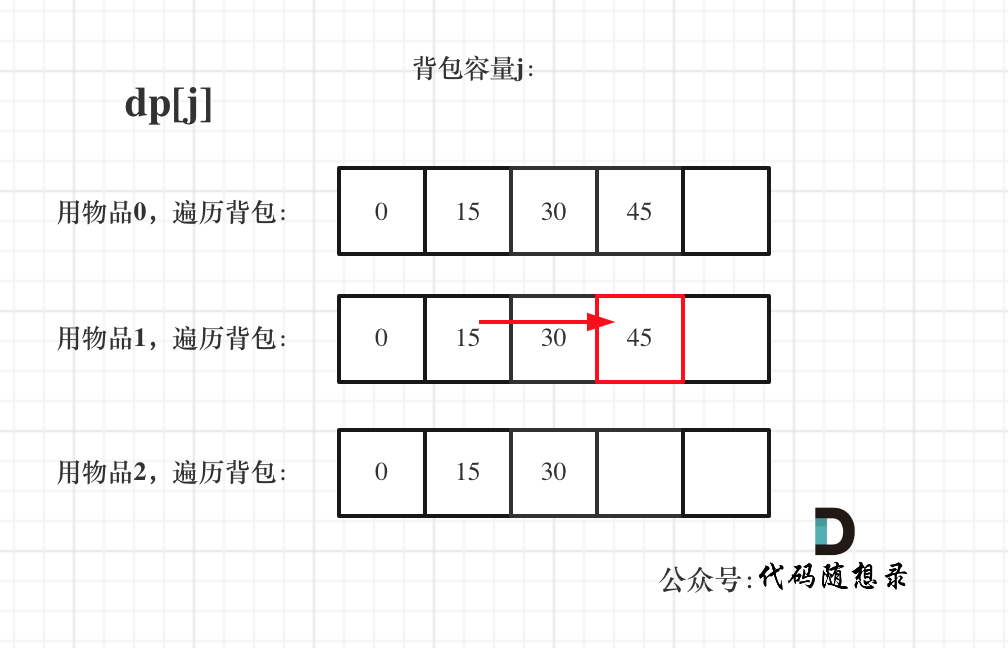
遍历背包容量在外层循环，遍历物品在内层循环，状态如图：

基础题目

509. 斐波那契数

力扣

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是： F(0) = 0，F(1) = 1 F(n) = F(n - 1) + F(n - 2)，其中 n > 1 给你n ，请计算 F(n) 。

dp := make([]int, n+1)
dp[0] = 0
dp[1] = 1
for i := 2; i <= n; i++ {
    dp[i] = dp[i-1] + dp[i-2]
}

62. 不同路径

力扣

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。问总共有多少条不同的路径？

dp[i][j]
dp[0~m-1][0] = 1, dp[0][0~n-1] = 1
for i := 1; i < m; i++ {
    for j := 1; j < n; j++ {
        dp[i][j] = dp[i][j-1] + dp[i-1][j]    
    }
}

343. 整数拆分

力扣题目链接

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

dp[i] = make([]int, n+1)
dp[0] = 0, dp[1] = 0, dp[2] = 1
for i := 3; i <= n; i++ {    // 遍历物品
    for j := 1; j < i - 1; j++ {
        dp[i] = max(dp[i], (i-j)*j, dp[i-j]*j)
    }
}