OO第一单元总结
第一单元解决的主要是表达式化简的问题,涉及到了因子、项和表达式三个层级。每一次的作业就是对于因子层不断增加新内容。第一次作业的因子有且仅有幂函数、常数和表达式因子;第二次作业新增了自定义函数、求和函数和三角函数因子;第三次作业是在第二次作业的基础上进行扩容,允许多层括号嵌套、允许三角函数括号內部进行因子嵌套,也允许多重自定义函数嵌套。其总的形式化表述如下所示(这里偷懒就直接把第三次作业指导书上的内容搬了过来):
-
表达式 \rightarrow 空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项
-
项 \rightarrow [加减 空白项] 因子 | 项 空白项 '*' 空白项 因子
-
因子 \rightarrow 变量因子 | 常数因子 | 表达式因子
-
变量因子 \rightarrow 幂函数 | 三角函数 | 自定义函数调用 | 求和函数
-
常数因子 \rightarrow 带符号的整数
-
表达式因子 \rightarrow '(' 表达式 ')' [空白项 指数]
-
幂函数 \rightarrow (函数自变量|'i') [空白项 指数]
-
三角函数 \rightarrow 'sin' 空白项 '(' 空白项 因子 空白项 ')' [空白项 指数] | 'cos' 空白项 '(' 空白项 因子 空白项 ')' [空白项 指数]
-
指数 \rightarrow '**' 空白项 ['+'] 允许前导零的整数
-
带符号的整数 \rightarrow [加减] 允许前导零的整数
-
允许前导零的整数 \rightarrow (0|1|2|…|9){0|1|2|…|9}
-
空白项 \rightarrow {空白字符}
-
空白字符 \rightarrow
(空格) |\t -
加减 \rightarrow '+' | '-'
-
自定义函数定义 \rightarrow 自定义函数名 空白项 '(' 空白项 函数自变量 空白项 [',' 空白项 函数自变量 空白项 [',' 空白项 函数自变量 空白项]] ')' 空白项 '=' 空白项 函数表达式
-
函数自变量 \rightarrow 'x' | 'y' | 'z'
-
自定义函数调用 \rightarrow 自定义函数名 空白项 '(' 空白项 因子 空白项 [',' 空白项 因子 空白项 [',' 空白项 因子 空白项]] ')'
-
自定义函数名 \rightarrow 'f' | 'g' | 'h'
-
求和函数 \rightarrow 'sum' '(' 空白项 'i' 空白项',' 空白项 常数因子 空白项 ',' 空白项 常数因子 空白项 ',' 空白项 求和表达式 空白项 ')'
-
函数表达式 \rightarrow 表达式
-
求和表达式 \rightarrow 因子
二、设计思路
第一次作业
第一次作业相对来说较为简单,因为其仅仅涉及了常数和幂函数。个人思路也比较清晰,为了便于化简,我使用了一个Hashmap来保存键值对,key值代表幂次,value值代表系数。值得注意的是这里为了避免被大数据定点爆破,value值需要使用Biginteger,而key由于课程题目的设置直接使用int类型即可。
第二次作业
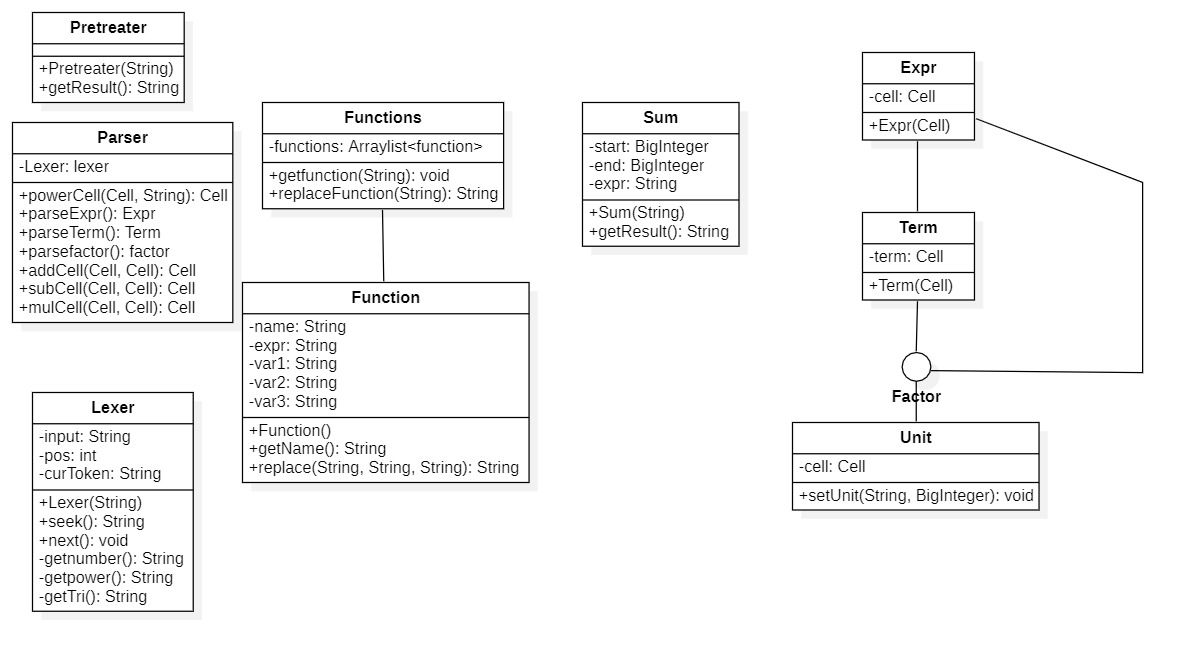
第二次作业的要求相比第一次作业来说有一个极大的提升。对我个人来说,主要的难点在于如何存储数据。在第一次作业中,可以直接使用多项式特有的“系数-指数”特性来利用Hashmap存储,但是在第二次作业中,由于新增了三角函数,所以之前的策略不再可行。为了找到一种统一的存储方式以便进行化简,我和很多同学进行了讨论,最后我决定使用嵌套Hashmap的方式进行操作。
内层的Hashmap如下所示
private HashMap<String,BigInteger> cell = new HashMap<>();
//String代表因子内容,可以是x或三角函数;Biginteger为其指数
对于Cell,我将其理解为一个细胞,也就是一个最小的存储单元。 可以注意到,它的key值使使用的String类型,这其实就是考虑到本次作业特点所做出的妥协。因为三角函数内部不会出现复杂的因子,所以只需要将三角函数进行一些预处理(比如说去掉常数的前导零和无用符号,去掉空白符),随后三角函数便可以转换为一个统一的形式。借助这种“范式”,我们就可以直接比较字符串来判断两个因子是否可以合并同类项。同时可以发现,Cell自带成为一个“项”的特性。当一个项里面需要多加入一个因子时,只需要往Cell中多插入一个键值对即可。
外层的Hashmap如下所示:
private HashMap<HashMap<String,BigInteger>,BigInteger> tissue = new HashMap<>();
//其实可以将其理解为HashMap<Cell,BigInteger>
//Cell即为刚刚所提及的“细胞”,而BigInteger为这个“细胞”前面的常数项系数
//整个tissue可以被理解为“系数*一个无系数的因子”的形式
可以观察到,外层的HashMap自带“表达式”特性。也就是说,tissue里面的一个键值对就是一个完整的项,当有多个键值对时,默认其中的关系为加法(或者减法),这样就组成了一个完整的表达式。
第二次作业UML图如下所示:
第三次作业
第三次作业是第二次作业的一个加强版,主要复杂在各种嵌套:括号嵌套、三角函数嵌套、自定义函数嵌套。身边很多同学都在极少代码改动的情况下轻松地完成了这次作业,但是我在这次作业中却被卡了许久。原因有以下两点:
-
在第二次作业中并没有解析求和函数和自定义函数而是直接在预处理阶段进行字符串替换
-
缺乏面向对象的思想,过度考虑计算的便利性而忽略了数据之间本身的结构关系。
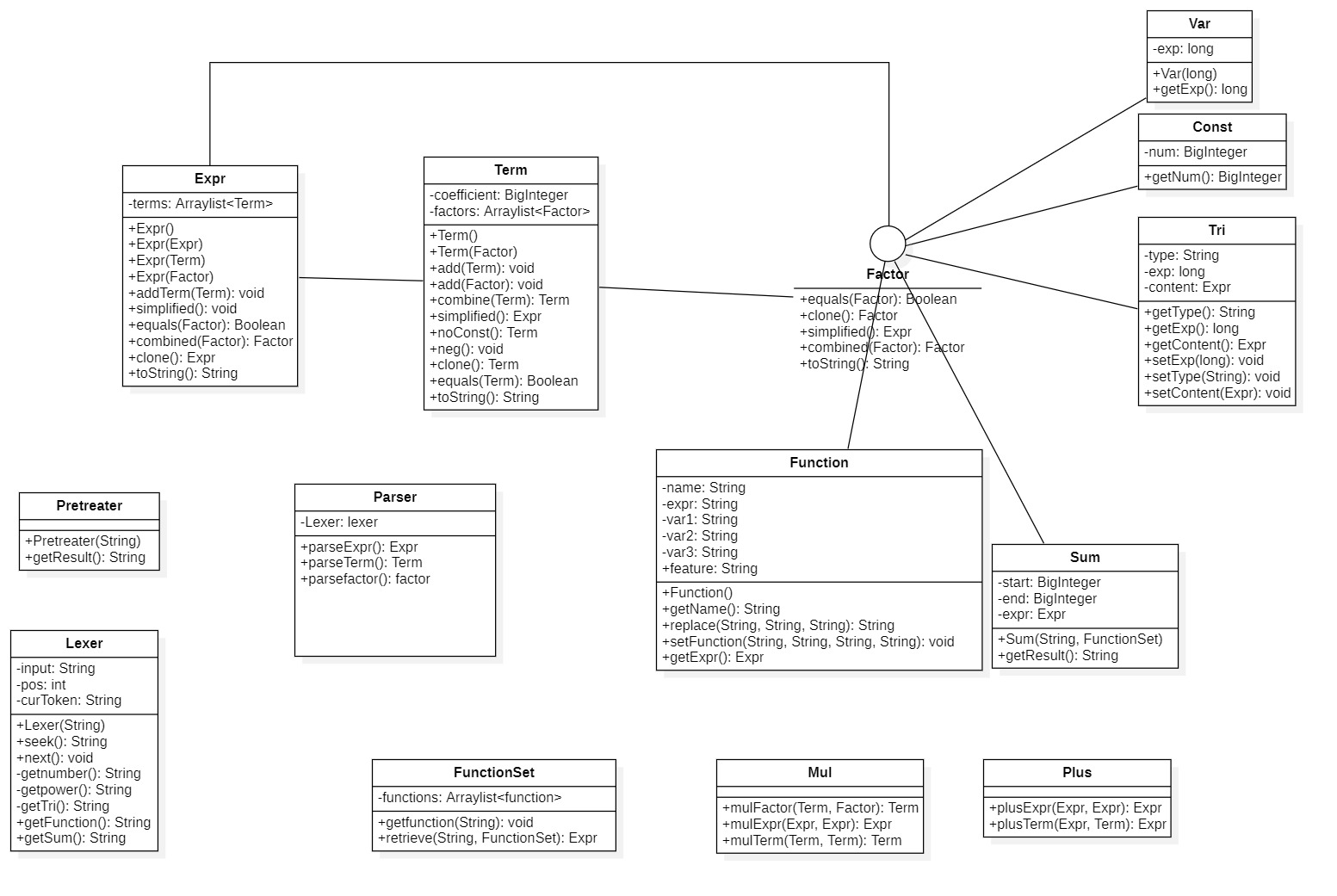
针对第一点,其实我就是在第二次作业偷懒了。考虑到求和函数和自定义函数都不允许嵌套,那我不就在句法分析之前直接预处理将他们全部替换掉即可?因此第二次作业当中我的预处理较为复杂,但却能尽可能地和第一次作业结构相似。但是由于允许函数嵌套,那就意味着我必须递归调用字符串替换,同时会引入相当多不必要的括号(为了保证替换时的正确性),给后期调试将带来极大的不便。因此在经过思考后,我还是决定不要偷懒,将自定义函数和求和函数单独生成一个类,作为因子参与到表达式化简的过程当中。
第二个问题其实才是最致命的。在第三周周一的理论课上,老师强调了“抽象层次结构”。说实话,在此之前我虽然知道自己在“面向对象”,但是从来不知道所面向的“对象”究竟是什么。在结合”多态“这个面向对象的核心概念之后,我突然”顿悟“了。没错,就是”顿悟“。我才意识到前两次作业我压根就没管过啥是对象,处于一种相当摇摆的状态,本质上我还是在使用某种”统一“的形式在进行操作,而忽略了对象本身的特点。具体来看,在第一次和第二次作业当中我其实并没有用到各个”类“的特性,而是都将他们用HashMap的形式表示在了一起,这虽然有利于合并计算化简,但是丢失了各个数据之间内在的层次结构关系。尤其是在老师讲述了”接口“的含义之后,我才真正理解了设置那么多子类究竟有何用处。通过多态的内部实现,我从外部可以直接管理一个”因子“类,其中的相等判断、乘法运算我都不用管具体实现细节如何,只需要知道这个”因子接口“中有这样的一个方法即可。在真正需要调用的时候,可以将选择权交给java,让java自己调用符合的子类的相应方法。
在经过了慎重的思考后,我决定抛弃第一第二次作业的架构,开始重构(重构势在必行!)
由于理解了面向对象真正的精妙之处,所以在重构的前半部分我走得很顺利。首先就是将各个因子类建好,考虑他们各自所必需的属性,并为他们定义一些常见的方法,使用factor这个接口来进行统一的管理。在句法和词法分析方面改动不大,只需要在分析时多考虑几种因子的情况即可。为了解决函数嵌套问题,我在三角函数、求和函数、自定义函数内部都进行了再一次的处理,即先将其内部的表达式解析并构建出一个表达式树,再将整个表达式树作为一个因子传回上一层级。使用类自身的调用可以有效的降低我思考的复杂度,避免了使用”循环“这种相对低端的方法来判断调用终点。
但是!构建表达式树不是真正的难点,真正的难点在于表达式化简。由于前两次我使用了Hashmap,并未真正地思考过表达式化简方面的问题,直接靠hashmap内部的机制就解决了。在重构时,我决定使用递归调用进行化简。整体思路很简单,无非就是表达式对化简过后的项求和,项对化简过后的因子求乘积。一开始上完理论课我就已经构思好整个架构了,觉得好像领悟到了《葵花宝典》的精髓,打通了任督二脉,体会到面向对象原来如此精妙。但是在实际操作的过程中,我发现了一个难点:究竟会递归到何处。每次在进行表达式之间化简运算的时候,我就会不由自主地往下想它下一层会如何调用,然后顺着这一层在接着往下想......用不了多久我就被绕晕了,所以这一块我一直没写对。
为了能够写对表达式运算模块,我请教了许多位大佬,最终意识到了自己的误区:在进行递归运算的时候不要想太多,只需要考虑递归的结束点以及每一层级我所需要的运算即可。也就是说,我在表达式层级只需要考虑将每个化简后的项进行加减运算即可,至于如何化简项就不是这一层级需要考虑的事情了。在递归的最底层,只需要考虑三角函数间、常数因子间以及幂函数因子间的化简即可。我想将他们定义为“原子因子”,因为无论是自定义函数还是求和函数抑或是表达式因子最终都会回归到“原子因子”上来。
在理清运算的递归关系之后,一切变得豁然开朗,剩下的就只是一些代码的实现了。第三次作业的UML图如下图所示。
三、代码度量
| Method | CogC | ev(G) | iv(G) | v(G) |
| calculate.Mul.mulExpr(Expr, Expr) | 3 | 1 | 3 | 3 |
| calculate.Mul.mulFactor(Term, Factor) | 9 | 1 | 5 | 5 |
| calculate.Mul.mulTerm(Term, Term) | 4 | 1 | 4 | 4 |
| calculate.Plus.plusExpr(Expr, Expr) | 2 | 1 | 3 | 3 |
| calculate.Plus.plusTerm(Expr, Term) | 9 | 1 | 5 | 5 |
| expr.Const.Const(String) | 0 | 1 | 1 | 1 |
| expr.Const.add(Const) | 0 | 1 | 1 | 1 |
| expr.Const.clone() | 0 | 1 | 1 | 1 |
| expr.Const.combined(Factor) | 2 | 2 | 2 | 2 |
| expr.Const.equals(Factor) | 1 | 2 | 2 | 2 |
| expr.Const.getNum() | 0 | 1 | 1 | 1 |
| expr.Const.mul(Factor) | 0 | 1 | 1 | 1 |
| expr.Const.same(Factor) | 0 | 1 | 1 | 1 |
| expr.Const.simplified() | 0 | 1 | 1 | 1 |
| expr.Const.toString() | 0 | 1 | 1 | 1 |
| expr.Expr.Expr() | 0 | 1 | 1 | 1 |
| expr.Expr.Expr(Expr) | 1 | 1 | 2 | 2 |
| expr.Expr.Expr(Factor) | 0 | 1 | 1 | 1 |
| expr.Expr.Expr(Term) | 0 | 1 | 1 | 1 |
| expr.Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| expr.Expr.clone() | 0 | 1 | 1 | 1 |
| expr.Expr.combined(Factor) | 0 | 1 | 1 | 1 |
| expr.Expr.equals(Factor) | 11 | 4 | 3 | 7 |
| expr.Expr.getTerms() | 0 | 1 | 1 | 1 |
| expr.Expr.simplified() | 1 | 1 | 2 | 2 |
| expr.Expr.toString() | 8 | 4 | 7 | 7 |
| expr.Function.clone() | 0 | 1 | 1 | 1 |
| expr.Function.combined(Factor) | 0 | 1 | 1 | 1 |
| expr.Function.equals(Factor) | 4 | 4 | 4 | 4 |
| expr.Function.getExpr() | 0 | 1 | 1 | 1 |
| expr.Function.getName() | 0 | 1 | 1 | 1 |
| expr.Function.replace(String, String, String) | 6 | 1 | 5 | 5 |
| expr.Function.setFunction(String, String, String, String, String) | 0 | 1 | 1 | 1 |
| expr.Function.simplified() | 0 | 1 | 1 | 1 |
| expr.FunctionSet.getfunction(String) | 1 | 1 | 2 | 2 |
| expr.FunctionSet.retrieve(String, FunctionSet) | 13 | 5 | 9 | 10 |
| expr.Sum.Sum(String, FunctionSet) | 13 | 1 | 4 | 7 |
| expr.Sum.clone() | 0 | 1 | 1 | 1 |
| expr.Sum.combined(Factor) | 0 | 1 | 1 | 1 |
| expr.Sum.equals(Factor) | 4 | 4 | 4 | 4 |
| expr.Sum.getExpr() | 0 | 1 | 1 | 1 |
| expr.Sum.getResult() | 11 | 2 | 6 | 7 |
| expr.Sum.simplified() | 0 | 1 | 1 | 1 |
| expr.Term.Term() | 0 | 1 | 1 | 1 |
| expr.Term.Term(Factor) | 0 | 1 | 1 | 1 |
| expr.Term.add(Factor) | 0 | 1 | 1 | 1 |
| expr.Term.add(Term) | 1 | 1 | 2 | 2 |
| expr.Term.clone() | 1 | 1 | 2 | 2 |
| expr.Term.combine(Term) | 1 | 2 | 1 | 2 |
| expr.Term.equals(Term) | 9 | 6 | 4 | 6 |
| expr.Term.getCoe() | 5 | 3 | 3 | 4 |
| expr.Term.getCoefficient() | 0 | 1 | 1 | 1 |
| expr.Term.getFactors() | 0 | 1 | 1 | 1 |
| expr.Term.neg() | 0 | 1 | 1 | 1 |
| expr.Term.noConst() | 3 | 3 | 2 | 3 |
| expr.Term.setCoefficient(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Term.setFactors(ArrayList) | 0 | 1 | 1 | 1 |
| expr.Term.simplified() | 2 | 1 | 2 | 3 |
| expr.Term.toString() | 6 | 2 | 4 | 4 |
| expr.Tri.Tri() | 0 | 1 | 1 | 1 |
| expr.Tri.Tri(String, FunctionSet) | 12 | 3 | 3 | 8 |
| expr.Tri.clone() | 0 | 1 | 1 | 1 |
| expr.Tri.combined(Factor) | 3 | 4 | 1 | 4 |
| expr.Tri.equals(Factor) | 10 | 5 | 4 | 5 |
| expr.Tri.getContent() | 0 | 1 | 1 | 1 |
| expr.Tri.getExp() | 0 | 1 | 1 | 1 |
| expr.Tri.getType() | 0 | 1 | 1 | 1 |
| expr.Tri.same(Factor) | 2 | 2 | 3 | 3 |
| expr.Tri.setContent(Expr) | 0 | 1 | 1 | 1 |
| expr.Tri.setExp(long) | 0 | 1 | 1 | 1 |
| expr.Tri.setType(String) | 0 | 1 | 1 | 1 |
| expr.Tri.simplified() | 1 | 2 | 1 | 2 |
| expr.Tri.toString() | 7 | 2 | 4 | 5 |
| expr.Var.Var(long) | 0 | 1 | 1 | 1 |
| expr.Var.clone() | 0 | 1 | 1 | 1 |
| expr.Var.combined(Factor) | 1 | 2 | 1 | 2 |
| expr.Var.equals(Factor) | 2 | 2 | 2 | 2 |
| expr.Var.getExp() | 0 | 1 | 1 | 1 |
| expr.Var.simplified() | 1 | 2 | 1 | 2 |
| expr.Var.toString() | 4 | 4 | 4 | 4 |
| src.Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| src.Lexer.getFunction() | 7 | 3 | 3 | 6 |
| src.Lexer.getNumber() | 2 | 1 | 3 | 3 |
| src.Lexer.getPower() | 6 | 2 | 6 | 6 |
| src.Lexer.getSum() | 7 | 3 | 3 | 6 |
| src.Lexer.getTri() | 7 | 3 | 3 | 6 |
| src.Lexer.next() | 11 | 2 | 12 | 13 |
| src.Lexer.seek() | 0 | 1 | 1 | 1 |
| src.MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| src.Parser.Parser(Lexer, FunctionSet) | 0 | 1 | 1 | 1 |
| src.Parser.parseExpr() | 4 | 1 | 3 | 3 |
| src.Parser.parseFactor() | 9 | 7 | 7 | 7 |
| src.Parser.parseTerm() | 23 | 1 | 12 | 12 |
| src.Pretreater.Pretreater(String) | 0 | 1 | 1 | 1 |
| src.Pretreater.getResult() | 0 | 1 | 1 | 1 |
| Class | OCavg | OCmax | WMC | |
| calculate.Mul | 4 | 5 | 12 | |
| calculate.Plus | 4 | 5 | 8 | |
| expr.Const | 1.2 | 2 | 12 | |
| expr.Expr | 2.27 | 7 | 25 | |
| expr.Function | 1.88 | 5 | 15 | |
| expr.FunctionSet | 5.5 | 9 | 11 | |
| expr.Sum | 2.86 | 6 | 20 | |
| expr.Term | 2.12 | 6 | 34 | |
| expr.Tri | 2.36 | 7 | 33 | |
| expr.Var | 1.86 | 4 | 13 | |
| src.Lexer | 3.88 | 9 | 31 | |
| src.MainClass | 2 | 2 | 2 | |
| src.Parser | 5.75 | 12 | 23 | |
| src.Pretreater | 1 | 1 | 2 | |
| Package | v(G)avg | v(G)tot | ||
| calculate | 4 | 20 | ||
| expr | 2.24 | 168 | ||
| src | 4.6 | 69 | ||
| Module | v(G)avg | v(G)tot | ||
| homework_2022_20373354_hw_3 | 2.71 | 257 | ||
| Project | v(G)avg | v(G)tot | ||
| project | 2.71 | 257 | ||
四、BUG分析
1、自身的bug
(1)第一次作业
可能是第一次作业较为简单的缘故,自己在第一次作业中没有出现bug。
(2)第二次作业
在第二次作业中,我的强测错了六个点,涉及到两个bug。其中第一个bug最为可惜,直接导致强测错了五个点。第一个错误出现在正则表达式。在本人第二次作业的思路中,已经提及了将各个因子转换为标准形式,然后使用字符串进行相应的操作。可是在生成字符串时,我忽略了自定义函数的代入问题。
f(x)=sin(x)
f(x**2)
//实际替换形式为:sin((x**2))
为了保证正确性,在函数调用时我会新增一对括号,可是在生成三角函数标准字符串时我的正则表达式忽略了这个括号,直接导致有这五个强测点的三角函数都是异常输出,即上述例子会输出
sin()
就因为这个正则五个强测点没了www。
另一个设计优化问题。我在优化输出时将sin(0)直接转换为0,将cos(0)直接转换为1,可是我大意了,忽略了三角函数后还有幂次的情况,导致了形如
原始输出:cos(0)**3
优化过后输出:1**3
问题就在于自己忽视了形式化表述,优化过后的输出其实是非法的,常数因子不能直接带上指数,这就让我有一个强测点出现了format error
(3)第三次作业
在第三次作业中,强测没出现问题,而互测被打了两刀。这其中出现了两个bug。第一个bug还是出现在正则表达式。在三角函数的输出判断中,为了减少输出长度,我会判断三角函数括号内部的内容,而由于正则表达式错误,会出现如下问题:
//测试样例:sin((x+1))
//本人输出:sin(x+1) format error
//错误正则:
public static final Pattern VAR_RE = Pattern.compile("x\\*?\\*?\\+?\\d+?");
//正确正则
public static final Pattern VAR_RE = Pattern.compile("x(\\*\\*\\+?\\d+)?");
我在此处的正则直接沿用了HW2的三角函数正则,那时候由于三角函数内部因子限制所以没有问题,但是在HW3由于因子种类扩大,之前的正则就会出现误判,导致我输出少了必要的括号。
第二个问题是判断表达式相等的过程中,如果出现两个表达式项的个数不相等时,可能会出现误判。
(4)总结
自身问题主要出现在正则表达式。这提醒我正则表达式虽好,但是也有风险,所以在使用正则表达式时一定要考虑充分,不然可能在意想不到的地方被人爆破。
2、他人的bug
他人的bug主要有以下三类:
首先是空串输出问题。当表达式的结果为零时,由于输出的一些优化可能会导致代码输出空串而没有输出0
其次是“逆向优化”问题。为了优化,少数同学将sin函数内部的负号提出括号外,却忽略了平方等偶次幂运算的特点,导致了输出时多了一个负号。
还有就是正则表达式的老大难问题。在第二次作业中有两个同学的三角函数内部正则表达式出现了偏差,大概情况如下
本意:将sin(x**1)替换为x
错误数据:sin(x**11)
错误输出结果:sin(x1)




