计算几何详解

计算几何基础

向量

基础概念

可以这么理解：既有长度又有方向的量。通常用 \(\overrightarrow{a}\) 表示。

运算

对于 \(\overrightarrow{a}=(x_1,y_1),\overrightarrow{b}=(x_2,y_2)\)：

• 加减法：\(\overrightarrow{a}\pm\overrightarrow{b}=(x_1\pm y_1,x_2\pm y_2)\)。几何意义为坐标平移。

• 点积：\(\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos<\overrightarrow{a},\overrightarrow{b}>\)。几何意义为 \(\overrightarrow{b}\) 的长度乘上 \(\overrightarrow{a}\) 在 \(\overrightarrow{b}\) 上投影（做垂线）的长度。注意点积得到的是数而不是向量。

• 叉积：\(\overrightarrow{a}\times\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\sin<\overrightarrow{a},\overrightarrow{b}>\)。几何意义为 \(\overrightarrow{a}\) 和 \(\overrightarrow{b}\) 张成的平面的一个法向量。叉积同样得到的是数。

应用

这些应用在计算几何题目中都是十分基础、重要的内容，需要掌握。

1. 判断夹角

• 点积为 \(0\)，两向量垂直。

• 点积 \(<0\)，夹角大于 \(90^{\circ}\)。

• 点积 \(>0\)，夹角小于 \(90^{\circ}\)。

考虑 \(\cos\) 性质即可。

2. 判断位置关系

• 当 \(\overrightarrow{a}\times\overrightarrow{b}<0\) 时，\(\overrightarrow{b}\) 在 \(\overrightarrow{a}\) 顺时针方向。

• 当 \(\overrightarrow{a}\times\overrightarrow{b}>0\) 时，\(\overrightarrow{b}\) 在 \(\overrightarrow{a}\) 逆时针方向。

3. 判断两线段是否相交

先判 \(x,y\) 的范围是否相交。

若相交，再用叉积判断一条线段两个端点是否在另一条线段的同一侧。

4. 计算三角形面积

两向量叉积的绝对值除以 \(2\) 即可表示两向量中间三角形的面积。

5. 求线段交点

设 \(AB,CD\) 交于点 \(O\)，原点为 \(O'\)，则：

\[\overrightarrow{O'O}=\overrightarrow{O'A}+\frac{\overrightarrow{AC}\times\overrightarrow{CD}}{\overrightarrow{CD}\times\overrightarrow{AB}}\overrightarrow{AB} \]

面积法，平移作垂线相似即可证明。

6. 点到线段距离

假设求 \(C\) 到 \(AB\) 的距离。

如果 \(\angle CAB>90^{\circ}\) 或 \(\angle CBA>90^{\circ}\)，则答案为 \(\min(AC,BC)\)。

否则考虑面积法，算出三角形面积再除以底即为高（距离），答案为 \(\frac{|\overrightarrow{AC}\times\overrightarrow{BC}|}{AB}\)。

7. 点到直线垂足

设 \(C\) 到 \(AB\) 垂足为 \(H\)，则：

\[\overrightarrow{AH}=\frac{|\overrightarrow{AC}\cdot\overrightarrow{AB}|}{|\overrightarrow{AB}|^2}\overrightarrow{AB} \]

考虑点积的几何意义（向量投影）即可。

8. 旋转向量

将 \(\overrightarrow{a}=(x,y)\) 逆时针旋转 \(\theta\) 度，得到 \((x\cos\theta−y\sin\theta,y\cos\theta+x\sin\theta)\)。

证明考虑坐标，使用和角公式即可。

多边形基础

多边形面积

设多边形顶点按顺时针排列为：\(\overrightarrow{a_1}=(x_1,y_1),\overrightarrow{a_2}=(x_2,y_2),\cdots,\overrightarrow{a_n}=(x_n,y_n)\)，则它的面积为：

\[S={1\over 2}\left(\sum\limits_{i=1}^{n-1}a_i\times a_{i+1}+a_n\times a_1\right) \]

自适应辛普森法

可用于求任意图形的面积，比较玄学。

设 \(f(a)\) 表示图形与直线 \(x=a\) 的交的长度，则面积能写成积分的形式：

\[\int^R_L f(x)\,\text{d}x \]

我们尝试用二次函数去拟合这条直线。假设 \(f(x)\approx Ax^2+Bx+C\)，经过推式子（积分）得：

\[S=\frac{R-L}{6}\left(f(L)+f(R)+4f(\frac{L+R}{2})\right) \]

但是显然有很大的误差，我们考虑分治，每次用公式拟合，再递归计算左右区间，如果误差在可接受的范围内，那么就不再递归。

判断点在多边形内

判断点 \(P\) 是否在多边形 \(A\) 内。

我们在无穷远处随机一个点 \(Q\)，连接 \(PQ\)，看 \(A\) 与 \(PQ\) 相交的边数的奇偶性。正确性显然。

注意到会有端点在 \(PQ\) 上的神秘情况，实战可以多次随机。

判断点在凸多边形内

我们从一个端点出发向每个顶点连出射线，显然可以把平面分成若干个区域。我们二分点在哪个区域里，就能很容易判断点是否在多边形内了。

注意点有可能在所有区域之外，要特殊判断。

例题

1. 折纸

给定一个正方形纸片和 \(8\) 条直线，按照直线依次翻折纸片（右侧翻到左侧上），\(50\) 次询问折叠后的某个点上有几层纸片。

sol:

我们考虑对于每一个询问点处理。容易想到折转化为展开。依次处理每条线，我们搜索当前点展开后能到达的所有位置。显然求出它展开一次后变成的两个点（求对称点），然后对于两个点继续搜索即可。最后处理完所有线后，把合法点统计进答案即可。复杂度 \(O(2^8)\)。

计算几何

凸包

基础概念

满足能围住平面上一些点的最小多边形。容易证明它一定是凸的（内角小于 \(180^{\circ}\)）。

Andrew 算法

先按 \(x\) 为第一关键字，\(y\) 为第二关键字排序。显然到第一个点一定在凸包内。

然后正反扫两遍，第一次求出上凸包，第二次求出下凸包。

以求上凸包为例，维护一个栈，假设加入一个点后不满足凸包的性质（没有"向右偏"）就将栈顶的点出栈。

例题

1. 信用卡凸包

信用卡是一个矩形，唯四个角作了圆滑处理，使它们都是与矩形的两边相切的 \(1/4\) 圆。现在平面上有一些规格相同的信用卡，试求其凸包的周长。

sol:

如下图：

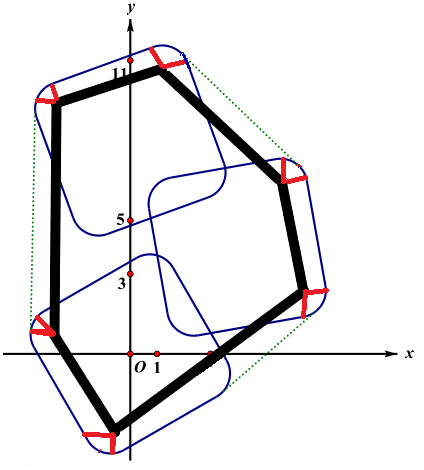
容易发现红色的圆弧刚好能拼成一个圆（转了一圈转回来了），剩下的黑色部分又是一个凸包，直接把每个信用卡建 \(4\) 个点，跑凸包板子即可。

2. timeismoney

给出一个 \(n\) 个点 \(m\) 条边的无向图，第 \(i\) 条边有两个权值 \(a_i\) 和 \(b_i\)。

求该图的一棵生成树 \(T\) ，使得

\[\left(\sum\limits_{e\in T}a_e\right)\times\left( \sum\limits_{e\in T}b_e\right)\]

最小。

sol:

将 \(\sum a\) 和 \(\sum b\) 分别看成 \(x\) 坐标和 \(y\) 坐标，并将它投射到平面直角坐标系上，那么我们就是想找到 \(x×y\) 最小的点，显然应该在所有点组成的凸包上。

但是求出每种生成树 \(\sum a\) 和 \(\sum b\) 十分困难，于是我们考虑另外一种求凸包的方式：分治。

先找出 \(x\) 最小的点 \(A\) 以及 \(y\) 最小的点 \(B\)，接下来我们就需要求出一个点 \(C\)，使得 \(C\) 在 \(AB\) 左侧且 \(C\) 距离 \(AB\) 最远（显然在凸包上）。

转化一下，即让 \(S_{\triangle ABC}\) 最大，即 \(\overrightarrow{AB}\times\overrightarrow{AC}\) 最小（因为 \(\overrightarrow{AB}\times\overrightarrow{AC}<0\)）。考虑这个式子：

\[\begin{aligned}\overrightarrow{AB}\times\overrightarrow{AC}&=(x_B-x_A)(y_c-y_A)-(y_B-y_A)(x_C-x_A)\\&=(x_B-x_A)\times y_C+(y_A-y_B)\times x_C+y_Bx_A-x_By_A\end{aligned} \]

于是变成最小化 \((x_B-x_A)\times y_C+(y_A-y_B)\times x_C\)。把边权改为 \((x_B-x_A)\times b_i+(y_A-y_B)\times a_i\)，跑最小生成树即可得到 \(C\) 点。然后递归计算 \(AC\) 和 \(CB\) 即可。

根据期望分析，复杂度为 \(O(m\log m\sqrt{\ln n!})\)。

闵可夫斯基和

基础概念

对于点集 \(A\) 和 \(B\)，定义它们的闵可夫斯基和为:

\[A+B=\{(X_A+X_B,Y_A+Y_B)\mid(X_A,Y_A)\in A,(X_B,Y_B)\in B\} \]

也就是把 \(A\) 中的每个点沿着 \(B\) 中每个向量的方向平移，所得到的点集。

求法

我们先求出 \(A\) 和 \(B\) 分别的凸包。显然，它们凸包的闵可夫斯基和就是原来 \(A\) 和 \(B\) 的闵可夫斯基和。

观察下面这张图（来自 OI-Wiki）：

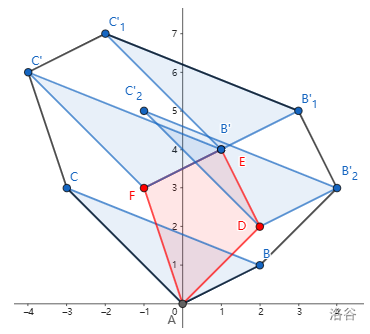
容易观察到，闵可夫斯基和 \(A+B\) 的边集是由凸包 \(A,B\) 的边按极角排序后连接的结果。于是我们将 \(A,B\) 极角排序，把 \(A_1+B_1\) 看做 \(A+B\) 的起点，然后用类似归并的做法依次放边即可。

例题

1. 战争

有两个凸包 \(P,Q\)，平移若干次 \(Q\)，问每次移动后是否有交点。

sol:

假设移动向量为 \(w\)。如果移动后有交点，那么一定存在 \(a\in A,b\in B\) 使得 \(b+w=a\)，变形一下得到 \(w=a−b\)。

于是可以构造闵可夫斯基和 \(C=A+(−B)\)（\(-B\) 是 \(B\) 的坐标都取反后的结果）。

转化为判断移动向量是否在 \(C\) 内，二分即可。

旋转卡壳

思路

似乎更偏向于是一种处理问题的思想。本质上就是双指针。

以求凸包直径为例，我们顺序枚举每个点 \(i\)，并处理以 \(i\) 为一个端点的最长直径。显然这条最长直径的另一个端点在 \(i\) 增加时，位置也会单调增加，于是维护一个指针，每次跳即可。

例题

1. 最大土地面积

给定 \(n\) 个点，选出四个点使得组成的四边形面积最大。

sol:

首先求出凸包，并特殊判断大小 \(\le 3\) 的情况。对于凸包大小 \(\ge 4\)，显然选出的四个点都在凸包上。

考虑枚举四边形的对角线。注意这里不需要每两对点全部枚举，只需枚举一个端点，并类似旋转卡壳求出距离它最远的点作另一个端点即可。

对于每一条对角线，我们需要计算出它两边距离它最远的两个点（作为四边形另外两个顶点）。我们发现这个东西在对角线顺序移动的时候也是单调的，于是使用指针维护即可。

2. 最小矩形覆盖

给定 \(n\) 个点，求框住所有点的最小矩形（矩形边不一定平行于坐标轴）。

sol:

先求出凸包。考察这个最小矩形的性质：它一定有一条边在凸包上。

感性理解：如果每条边都不在凸包上，那么就可以把这个矩形旋转一下"卡在"凸包上，这时候就会多"节约"出来一些空，可以使答案更优。

于是我们顺序枚举每条凸包上的边作为矩形的一条边，然后旋转卡壳处理对于这条边最左、最上、最右的点即可。

半平面交

基础概念

半平面：一条直线左侧或右侧的平面。

半平面交即为所有半平面的交集。显然应该是一个凸多边形。

S&I 算法

我们维护当前半平面交的凸壳。因为后来加入的只可能会影响最开始加入的或最后加入的边，容易想到单调队列维护。

先把向量极角排序（也就是按照斜率排序），然后顺序枚举每个向量。对于当前枚举的向量，如果上一个交点在这条向量表示的半平面的异侧（如果半平面表示直线左侧的平面，那么"异侧"就代表右侧），那么显然上一条边就没有意义了。图片示例（来自 OI-Wiki，当前向量为 \(\vec{c}\)，交点为 \(D\)）：

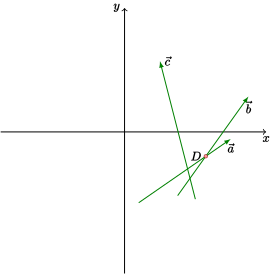
什么时候队首会被影响呢？考虑这样的情况：一开始的向量指向左下，枚举到后面时向量指向左上，这时最前面的交点在最后加入的向量表示半平面的异侧（和上图差不多的方位），那么就需要弹出队首。

于是就求出了半平面交的顶点。

这里有一个需要注意的点：我们需要先弹出队尾，再弹出队首。考虑一个向量，它能够弹出所有队列中的向量，如下图：

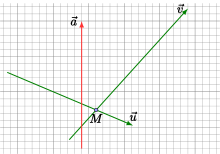
如果先弹出 \(\vec{u}\)，显然 \(\vec{a}\) 左边的半平面交会被扩大，错误计算（因为极角排序后 \(\vec{v}\) 的影响范围会更小）。

圆相关

最小圆覆盖

给定平面上 \(n\) 个点，求最小的圆使得覆盖所有点。

算法（随机增量法）

我们依次枚举每个点加入。考虑新加入一个点 \(p\) 对答案的影响：假设前面所有点的集合为 \(S\)，显然如果 \(p\) 不在 \(S\) 的最小覆盖圆内，那么 \(p\) 一定在 \(S\cup\{p\}\) 的最小覆盖圆上。

于是得到"暴力"算法：若 \(p\) 不在当前的最小覆盖圆上，就设当前最小覆盖圆为 \((p,0)\)，向前枚举一个点 \(i\)，若 \(i\) 不在当前最小覆盖圆内，则设新的最小覆盖圆为以 \(p,i\) 为直径端点的圆；然后再向前枚举一个点 \(j\)，若 \(j\) 不在当前最小覆盖圆内，则设当前最小覆盖圆为 \(p,i,j\) 的外接圆。

例题

1. 最小双圆覆盖

给定平面上 \(n\) 个点，求两个最小的半径相同的圆使得它们覆盖所有点。

sol:

仍然是考虑这两个圆的性质。显然两个圆一定是左边一个、右边一个，中间有一些覆盖的交集。我们发现最优的覆盖方法一定能够把点集分成两半，一半左边圆覆盖，一半右边圆覆盖。进一步地，观察到一定存在一条直线，使得点集分成的左右两半构成的覆盖方案是最优解。

于是考虑枚举这条直线，并在两边跑最小圆覆盖即可。考虑到点数不多，我们枚举直线的角度，并把坐标系旋转转化为竖直的直线，二分处理。枚举的角度精度可以多试一下。