WQS二分

简介

WQS 二分主要用来解决下面问题：给定 \(n\) 个物品，要求从中恰好选 \(m\) 次。对于一个选择方案，它有一个权值，请最大/最小化这个权值。以下假设题目要求最大权值。

使用它有一个条件：假设选择 \(i\) 个物品的最大权值为 \(f(i)\)，需要 \((i,f(i))\) 形成的图形是一个凸包。如下图（此图片及以下图片均来自此处，侵删）：

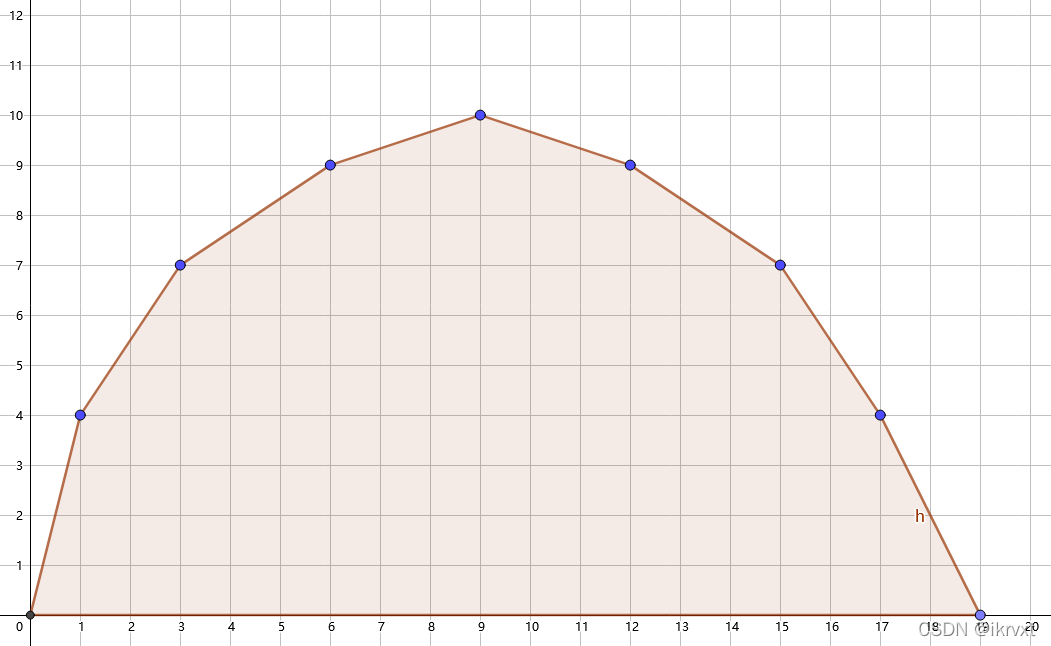
需要注意的一点是，我们并不知道这个凸包的形状，但知道这是个上凸包。我们需要利用这一点解决问题。

算法思路

我们考虑用直线去切凸包。具体来说，我们不断用斜率 \(k\) 不同的直线切，并能够处理出直线第一个碰到的点 \((x,f(x))\)。直到切到 \(x=m\)，就可以求出 \(f(m)\) 的值了。

这里，我们可以利用上凸包的性质：直线的 \(k\) 越大，切到的 \(x\) 就越靠左，具有单调性。于是可以二分。

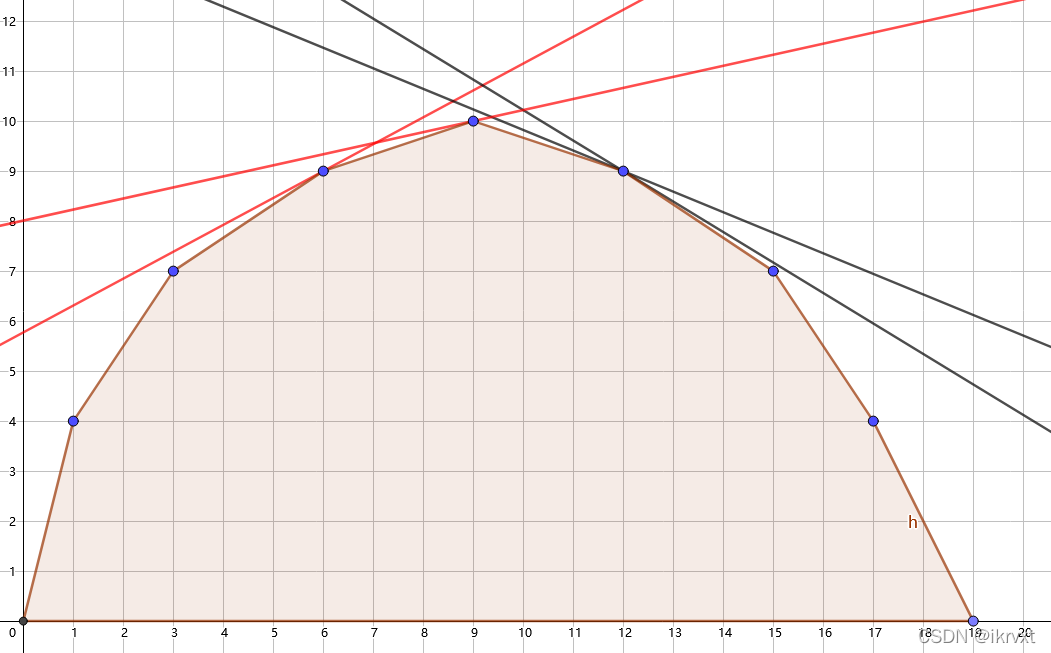
那么二分时，我们需要 check 什么呢？显然，我们需要找到最先切到的点。观察这条直线切每一个点的图像，我们发现：截距（与 \(y\) 轴的交点）最大的一条就是最先切到的一条。

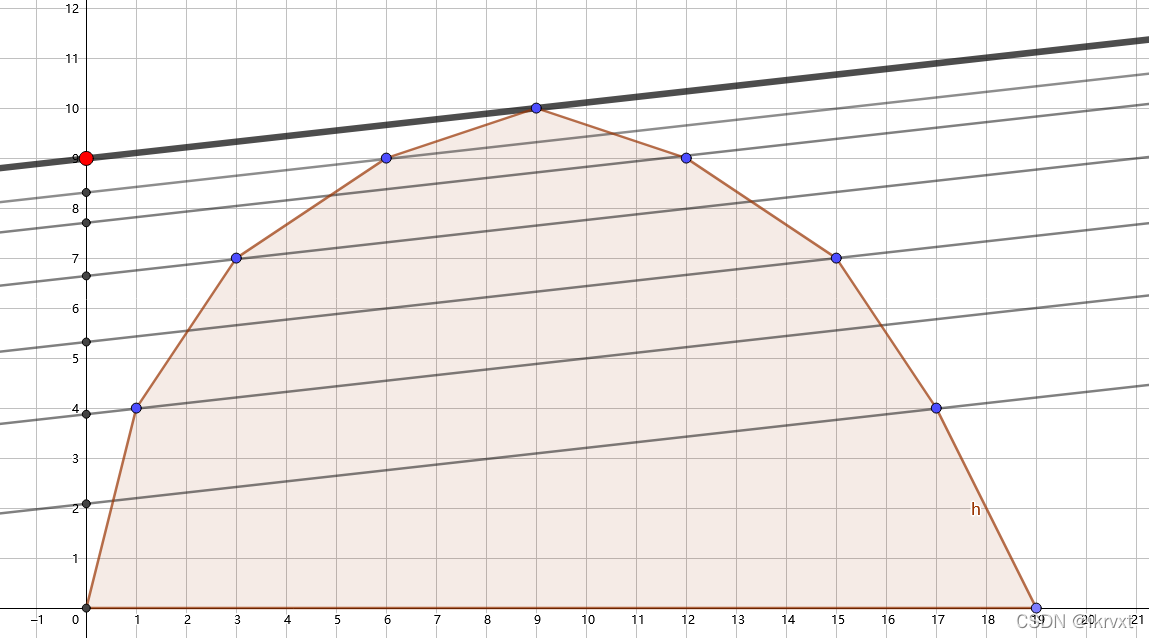
而一条斜率为 \(k\)，经过 \((t,f(t))\) 的直线方程为 \(y=kx+f(t)-kt\)，截距为 \(f(t)-kt\)。问题转化为对于所有 \(t\)，求出 \(f(t)-kt\) 的最大值。我们发现，这相当于每选一个物品会有 \(-k\) 的附加权值，然后求一遍无次数限制的最大值。到这一步，通常都能使用 DP 解决了。

而 check 过程中，一般都能处理出这条线切到的点的坐标，于是 \(f(m)\) 就能算了。

例题

1. Tree I

给你一个无向带权连通图，每条边是黑色或白色。请求出一棵恰好有 \(m\) 条白边的最小生成树。

sol:

发现这个问题完全满足 WQS 二分的条件，是一个上凸包。于是二分斜率 \(k\)，每条白边加上附加权值 \(-k\)。如果白边的数量少了，那么说明白边权较大，那么 \(k\) 要增大，反之亦然。二分即可。

2. 林克卡特树

给你一棵树，割掉恰好 \(k\) 条边然后重新接上恰好 \(k\) 条 \(0\) 权边，然后要求最大化新树的直径。

sol:

割掉 \(k\) 条边之后会出现 \(k+1\) 个联通块，那么我们对于每一个联通块求直径然后用 \(k\) 条边将这 \(k\) 个联通块串起来即可了。所以问题变成了在树上寻找 \(k+1\) 条不相交链，并且最大化这 \(k+1\) 条链的边权之和。

经过暴力 DP 再打表后，我们发现答案是上凸的！于是可以使用 WQS 二分去掉 \(k\) 的限制，每选一条链加上一个附加权值，后续的 DP 就非常简单了，这里略去。