字符串
AC 自动机
简介
AC 自动机可以解决:给定一个模式串集合和一个主串,求有多少个模式串在主串中出现。
AC 自动机是在 Trie 树上添加一些转移边(称为 \(\operatorname{fail}\))形成的。具体来说,一个节点 \(S\) 会连向 \(T\),代表 \(T\) 是 \(S\) 在 Trie 树上出现过的最长后缀。
构建方法
我们先构建出 Trie 树。接着,我们按照字符在 Trie 上的深度从小到大(就是 BFS 序)枚举节点处理 \(\operatorname{fail}\)。这样的好处是,我们在处理当前节点时,所有长度更短的串的 \(\operatorname{fail}\) 都已经计算好了。
假设当前枚举的节点为 \(u\),它的父亲为 \(p\),这条 Trie 的边的字符为 \(c\)。那么我们直接循环跳 \(p\) 的 \(\operatorname{fail}\),直到跳到的点 \(f\) 有 \(c\) 的出边或不能往上了为止。把 \(p\) 连向 \(f\) 点 \(c\) 出边指向的节点即可。
其实这个过程应该很好理解,\(u\) 在 Trie 上出现过的后缀就是 \(p\) 在 Trie 上出现过的后缀加上一个 \(c\) 字符,用 \(p\) 的 \(\operatorname{fail}\) 跳就行。
在代码实现上,我们如果 while 向上跳,可能会超时,这时我们采用一种压缩路径的方式,如果一个点 \(p\) 没有 \(x\) 的出边,我们就创建一个 \(x\) 的边指向 \(\operatorname{fail}_p\) 的 \(x\) 出边。这样以后跳到 \(p\) 时如果要找 \(x\) 出边,那么就可以省去中间一大段跳 \(\operatorname{fail}\) 的过程。看一张图:
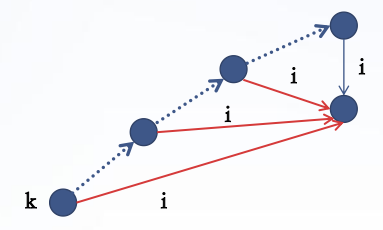
这样,AC 自动机的构建就完成了。
查询算法
一个一个枚举主串的字符,并在字典树上走。走到节点 \(p\) 时,不停跳它的 \(\operatorname{fail}\),统计答案即可。
Manacher
简介
Manacher 可以做到时间复杂度 \(O(n)\) 求最长回文子串及相关问题。
Manacher 的思想是利用前面求出的东西加速后面的计算。它产生的原因主要是因为回文串的特殊性:如果求出了 \(i-1\) 处的最长回文半径,那么这个回文串有可能延伸到 \(i\) 后面,可以帮助 \(i\) 的计算。
算法流程
首先,奇回文和偶回文不好处理,我们在每两个字符间加上 #,这样所有回文串都是奇回文了。
我们记录现在已知回文子串的最大右端点 \(R\),和它对应的回文中心 \(C\)(为了最大限度利用已知条件)。假设第 \(x\) 位的最长回文半径为 \(p_x\)。
假设现在处理到第 \(i\) 位。我们有两种情况:
-
若 \(i>R\),这时已有的条件无法帮助处理,暴力扩展即可。
-
若 \(i\le R\),我们发现,\(i'\) 的回文区域是我们已经求过的,于是我们就可以加速处理,放一张图:

我们需要分三种情况考虑:-
若 \(i'\) 的回文区域在 \([L,R]\) 内:

这时因为回文串翻转后还是回文串,而 \(i'\) 已经无法扩展了,于是 \(p_i=p_{i'}\)。 -
若 \(i'\) 的回文区域超过了 \(L\):

这时,显然 \(3\) 为 \(1\) 的反转,而 \(4\) 又为 \(3\) 的反转,所以 \(4\) 和 \(1\) 相同。
但是 \(2\) 一定不与 \(1\) 的反转相同(否则 \([L,R]\) 可以扩展),也就是说 \(2\) 一定不与 \(4\) 的反转相同,那么 \(i\) 只能扩展到 \(R\),即 \(p_i=R-i+1\)。 -
若 \(i'\) 的回文区域左端点刚好为 \(L\):

此时 \(2\) 是否等于 \(4\) 的反转未知,于是还是需要暴力扩展。
-
至此,Manacher 的流程已讲解完毕。但我们一定有一个疑问:算法中有这么多暴力扩展,为什么复杂度还是 \(O(n)\) 呢?
时间复杂度
使 Manacher 复杂度正确的东西主要是这个 \(R\):显然,它只增不减。但只有这一点还不够,我们需要说明每次操作要么是 \(R\) 加一,要么复杂度为 \(O(1)\)。我们对于每种情况考虑:
-
若 \(i>R\),显然扩展会使 \(R\) 增加。
-
若 \(i\le R\):前两种情况显然复杂度为 \(O(1)\)。对于第三种情况:若无法扩展,则复杂度为 \(O(1)\);若可以扩展,则会使 \(R\) 增加。
于是总复杂度为 \(O(n)\)。
回文自动机
简介
回文自动机可以在线性复杂度内求出字符串中所有的回文子串,和一些相关的问题。
回文自动机的每个节点都是一个回文子串,一条转移边代表在子串前后分别加上同一个字符。因为回文串有长度为奇数和偶数两种,所以回文自动机也有两个根,称为奇根、偶根,代表长度为 \(0\) 和 \(-1\) 的字符串(\(-1\) 可以理解为转移后是单个字符的子串)。
回文自动机采用的是一个一个添加字符,处理贡献的方式。那么,我们在添加字符时需要维护什么来方便建边呢?考虑串为 \(s\),当前加入第 \(i\) 个位置,前 \(i-1\) 个字符的最长回文后缀为 \([x,i-1]\)。如果 \(s_i=s_{x-1}\),显然 \([x-1,i]\) 就是新的最长回文串。否则,我们必须找出另一个以 \(i-1\) 结尾的回文串,判断它两边的字符是否相等。容易看出,我们维护每个节点的最长回文后缀,添加字符时不停跳即可。这也就是回文自动机 \(\operatorname{fail}\) 的定义。
构建方法
我们扫描一遍字符串,假设当前的位置为 \(i\),考虑在回文自动机中添加当前字符。
在这之前,我们已经处理了 \(i\) 之前的所有子串,并维护了每个节点 \(x\) 的回文串长度 \(len_x\)。假设处理完 \(i-1\) 后,跳到的节点为 \(l\)。
我们看 \(l\) 能否再扩展一个字符,也就是判断 \(s_i\) 和 \(s_{i-len_l-1}\) 是否相等。相等则可以在 \(l\) 下新建 \(s_i\) 的出边,否则不断跳 \(l\) 的 \(\operatorname{fail}\),直到条件满足即可。这一步可以参照简介理解。
这里有一个细节:如果跳到根节点了还无法扩展,那么怎么保证一定会加入 \([i,i]\) 这个字符串呢(单个字符一定是回文串)?我们可以把偶根的 \(\operatorname{fail}\) 连向奇根,而奇根的 \(len\) 为 \(-1\),一定可以扩展(因为 \(s_i\)=\(s_{i-(-1)-1}\)),于是问题解决。
现在我们已经新建了一个节点 \(cur\),如何连它的 \(\operatorname{fail}\) 指针?假设 \(l\) 不断跳 \(\operatorname{fail}\) 跳到了 \(p\),那么我们从 \(\operatorname{fail}_p\) 开始继续跳(因为 \(p\) 两边字符都是 \(s_i\)),直到某一个回文后缀有 \(s_i\) 的出边,把 \(cur\) 的 \(\operatorname{fail}\) 连向它即可。
时间复杂度
我们需要知道:每在字符串末尾增加一个字母,本质不同回文子串的数量至多会增加 \(1\)。
证明:我们选出增加的回文子串中最长的一个。如果还增加了其他的回文子串,则该回文子串必定在之前已经出现过,并非本质不同。看图理解:

那么,回文自动机中的节点是扩展了 \(n\) 次之后生成的,最多只有 \(n\) 个节点,所以回文自动机的时间复杂度为 \(O(n)\)。
后缀数组
简介
可以在 \(O(n\log n)\) 或 \(O(n)\) 的复杂度内,把一个字符串的所有后缀按字典序排序。
下面我们设 \(sa_i\) 表示将后缀排序后第 \(i\) 小的后缀开头的字符位置,\(rk_i\) 表示后缀 \(S_i\)(表示以 \(i\) 开头的后缀)的排名。
算法思路
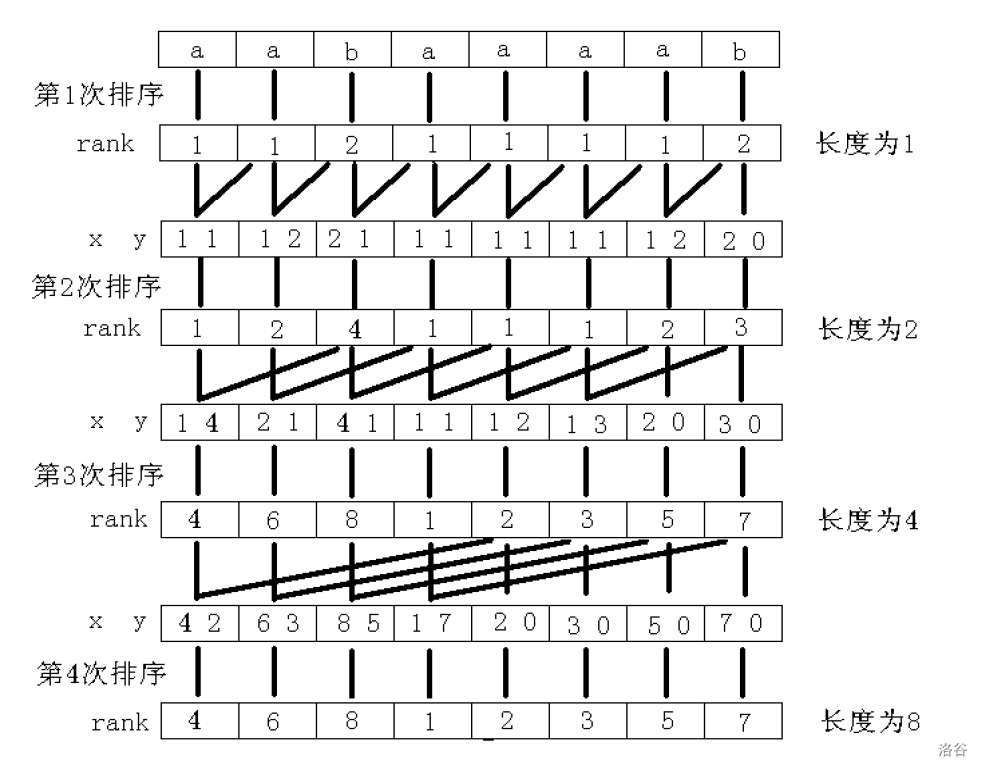
我们主要采用倍增的思想求后缀数组。
假设我们求出了长度为 \(w\) 的子串的排名 \(rk^w_i\),那么我们以 \(rk_i^w\) 为第一关键字,\(rk_{i+w}^w\) 为第二关键字排序,就可以求出 \(rk_i^{2w}\)。
这里,因为只有两个关键字,所以可以使用基数排序,复杂度从 \(O(n\log^2 n)\) 优化到 \(O(n\log n)\)。
应用
设 \(h_i=\operatorname{LCP}(S_{sa_{i-1}},S_{sa_i})\)。解释一下:\(sa_{i-1}\) 是第 \(i-1\) 小的后缀的开头字符,那 \(S_{sa_{i-1}}\) 就是第 \(i-1\) 小的后缀。于是 \(h_i\) 就是排名 \(i-1\) 和 \(i\) 的后缀的 \(\operatorname{LCP}\)。
我们使用后缀数组,可以 \(O(n)\) 求出 \(h\) 数组。
具体来说,定义 \(H_i=h_{rk_i}\)。\(rk_i\) 是后缀 \(S_i\) 的排名,根据 \(h\) 的定义,\(H_i\) 就表示后缀 \(S_i\) 和排在它前面一位的后缀的 \(\operatorname{LCP}\)。
\(H_i\) 有如下性质:
证明:
设 \(S_k\) 是 \(S_{i-1}\) 前一名的后缀,根据 \(H\) 的定义,它们的 \(\operatorname{LCP}\) 是 \(H_{i-1}\)。我们现在讨论 \(s_k\) 和 \(s_{i-1}\) 的关系(\(s\) 是原字符串):
-
若 \(s_k\ne s_{i-1}\),那么 \(H_{i-1}=0\),不等式显然成立。
-
若 \(s_k=s_{i-1}\),那么 \(S_{i}\) 和 \(S_{k+1}\) 的 \(\operatorname{LCP}\) 必然是 \(H_{i-1}-1\)(扣掉两个相同字符)。因为字典序排名相邻的串的 \(\operatorname{LCP}\) 最大,所以 \(S_i\) 和排名小于 \(S_i\) 的后缀的 \(\operatorname{LCP}\) 最大值为 \(H_i\)。而根据假设 \(rk_k<rk_{i-1}\),去掉第一个字符得到 \(rk_{k+1}<rk_i\),于是 \(S_{k+1}\) 的排名小于 \(S_i\),\(\operatorname{LCP}(S_{k+1},S_{i})\) 也必须小于上界 \(H_i\),即 \(H_i\ge H_{i-1}-1\)。
后缀自动机
定义
字符串 \(s\) 的 SAM 是一个接受 \(s\) 所有后缀的最小 DFA(确定性有限状态自动机)。
可以理解为在 SAM 上走可以经过 \(s\) 的所有后缀。
字符串的 \(\operatorname{endpos}\)
设字符串 \(s\) 的一个非空子串 \(s'\) 在 \(s\) 中所有结尾的位置构成的集合为 \(\operatorname{endpos}\)。
\(\operatorname{endpos}\) 有一些性质:
-
对于 \(s\) 的两个非空子串 \(a,b(|a|\le |b|)\),如果 \(\operatorname{endpos}(a)=\operatorname{endpos}(b)\),那么 \(a\) 是 \(b\) 的后缀;如果 \(a\) 是 \(b\) 的后缀,则 \(\operatorname{endpos}(b)\subseteq \operatorname{endpos}(a)\),否则 \(\operatorname{endpos}(a)\cap \operatorname{endpos}(b)=\empty\)。
这个十分显然,因为如果 \(a\) 是 \(b\) 的后缀,\(b\) 出现的地方 \(a\) 一定出现,\(a\) 出现的地方 \(b\) 不一定出现。 -
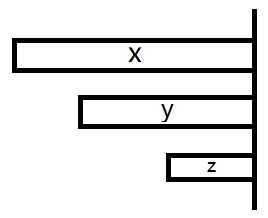
同一个 \(\operatorname{endpos}\) 等价类中的字符串的长度互不相同且连续。
考虑两个串 \(x,y(|x|>|y|)\),她们在同一个等价类中。那么对于一个串 \(z\) 满足 \(|x|>|z|>|y|\) 且 \(z\) 是 \(x\) 后缀,因为 \(x\) 出现的地方 \(z\) 一定出现,所以 \(z\) 的 \(\operatorname{endpos}\) 包含 \(x\) 的 \(\operatorname{endpos}\);而 \(z\) 出现的地方 \(y\) 一定出现,所以 \(z\) 的 \(\operatorname{endpos}\) 属于 \(y\) 的 \(\operatorname{endpos}\)。于是 \(z\) 一定和 \(x,y\) 在同一个等价类中。
放一张图:
Parent 树(后缀链接)
对于一个字符串,我们如果不断在前面添加字符,那么它的 \(\operatorname{endpos}\) 会逐渐变小,添加不同的字符会使 \(\operatorname{endpos}\) 划分为几个不交的集合。我们把这个划分建成一棵树的形态,这就是 parent 树,每个节点都对应了一些字符串和一个 \(\operatorname{endpos}\) 集合(就是一个 \(\operatorname{endpos}\) 等价类)。
反过来看,对于一个等价类中的串,它的父亲就应该是不在这个等价类中的最长后缀所在的节点(相当于不断删除这个等价类中最长串的开头字符,直到它的 \(\operatorname{endpos}\) 变化,得到的串就是它的父亲节点)。
因为是不断划分的,所以这棵树最多有 \(2n-1\) 个点。
另一个结论:一个节点中包含了一些长度连续的字符串,设最长串的长度为 \(l_u\),最短串的长度为 \(ml_u\),则有 \(ml_u=l_{fa_u}+1\)。
SAM 的构造
SAM 是一个 DAG,而 SAM 中的节点就是 parent 树上的节点(注意边和 parent 树上不一样)。现在要做的就是在树上添加边使得其能接受所有后缀。将一个节点连向另一个节点,表示这个节点中所有串在后面加上一个字符后会到达另一个 \(\operatorname{endpos}\) 等价类(这里容易理解错,正确意思是这个节点的所有串同时加上一个字符后,它们的 \(\operatorname{endpos}\) 集合两两还是一样的,只是可能和加上之前的 \(\operatorname{endpos}\) 集合不同)。
现在考虑如何在线性复杂度内构造 SAM,我们将所有字符依次加入 SAM 中。在加入第 \(i\) 个字符时,已经维护好了 \([1,i-1]\) 这个串构成的 SAM。我们记 \(ls\) 表示前缀 \(i-1\) 对应的节点。
当插入第 \(i\) 个字符(假设是字符 \(c\))时,新建一个点 \(k\) 表示整个串对应的节点。我们从 \(ls\) 开始,一直在 parent 上跳父亲,如果这个点没有 \(c\) 的出边,就将其连向 \(k\),直到跳到一个有 \(c\) 出边的点 \(p\),或者跳到了根节点。
为什么要这么做?考虑插入当前字符对后缀树的影响:对于串 \([1,i-1]\) 的每一个后缀 \([t,i-1]\),它的后面都添加了字符 \(c\)。我们从 \(ls\) 开始跳父亲,相当于把 \([1,i-1]\) 的每一个后缀按不同的等价类分成了若干不交部分枚举。考虑枚举到了一个等价类(节点),它里面字符串的 \(\operatorname{endpos}\) 集合都是 \(S\)。这时我们按照它有没有 \(c\) 的出边分为两种情况:
-
它没有 \(c\) 的出边。这说明集合 \(S\) 中的每个位置后面都没有字符 \(c\),而现在在最后添加了一个 \(c\)(\(S\) 中必然包含 \(i-1\)),所以直接把节点连向 \(k\) 即可。
-
它有 \(c\) 的出边。因为我们是从 \(ls\) 开始向上跳父亲,所以我们枚举的集合 \(S\) 会越来越大,再往上跳一定都有 \(c\) 的出边,所以直接跳出循环即可。
如果是跳到了根节点且还没有出边,这就说明之前整个字符串没有字符 \(c\),将 \(k\) 的父亲设为 \(1\)。
否则,假设我们跳父亲跳到了 \(p\),设它通过 \(c\) 出边可以转移到 \(q\)(注意到 \(p\) 是 \(s\) 最长的、且满足 \(p+c\) 在前 \(i-1\) 个字符组成的串中出现过的后缀)。显然我们不应该在这里添加一个新的 \(c\) 的转移。
然而,我们的难点在于,\(k\) 的父亲应该连接到哪个状态呢?我们要把父亲连到一个状态上,且其中最长的一个字符串恰好是 \(p+c\),即这个状态的 \(l\) 应该是 \(l_p+1\)(父亲的定义是在前面删字符去到不同等价类,而因为上面标黑的那句话,\(p+c\) 是最长的去到不同等价类里的一个后缀,于是易得此结论)。我们讨论 \(l_p\) 和 \(l_q\) 的关系:
-
如果 \(l_q=l_p+1\),那么 \(q\) 满足上面的条件,我们只需要将 \(k\) 的父亲连向 \(q\) 即可。
-
否则 \(l_q>l_p+1\),这意味着 \(q\) 中不止有长度为 \(l_p+1\) 的串,还有更长的串。这种情况下,我们必须通过拆开 𝑞 来创建一个新节点,使得它的 \(l\) 等于 \(l_p+1\)。
我们如何拆开一个状态呢?我们复制 \(q\),产生一个状态 \(cl\),我们将 \(l_{cl}\) 赋值为 \(l_p+1\)。由于我们不想改变遍历到 \(q\) 的路径,我们将 \(q\) 的所有转移复制到 \(cl\)。我们也把 \(cl\) 的父亲连向 \(q\) 的父亲,并把 \(q\) 的父亲连向 \(cl\)。
在拆开状态后,我们就可以把 \(k\) 的父亲连向 \(cl\) 了。最后,我们还需要把一些到 \(q\) 的转移重定向到 \(cl\)。从 \(p\) 开始跳父亲,直到根节点或者转移到不是状态 \(q\) 停止,把一路上的全部重定向即可。
以上就是 SAM 的构建过程。对于复杂度,SAM 的点数最多为 \(2n-1\),边数最多为 \(3n-4\),构建的时间复杂度为 \(\mathcal{O}(n)\)。另外,如果字符集很大,那么每个节点可以维护一个 map 来记录出边。
例题
基础
- 最小表示法
求一个字符串 \(s\) 循环移位后字典序最小的一个。
sol:
相当于求字符串 \(s+s\) 长度为 \(|s|\) 的子串中字典序最小的。建出 SAM,从根节点开始,走 \(|s|\) 次最小的字符即可。
- 不同子串个数
给你一个长为 \(n\) 的字符串,求本质不同的子串的个数。
sol:
建出 SAM,相当于统计路径条数,拓扑序上 DP 即可。
还有一种在线的方法:假设每次新加的点为 \(x\),那么答案加上 \(l_x-l_{f_x}\)。这是生成魔咒的做法。
- 弦论
给定一个字符串,求出它的第 \(k\) 小子串是什么。不同位置的相同子串有可能算作一个或多个。
sol:
建出 SAM,从根节点开始走。对于每个点 \(x\),我们维护一个 \(f_x\) 表示经过 \(x\) 的位置不同子串数量。走的过程类似线段树查询第 \(k\) 小的过程。
如何维护 \(f\)?如果本质不同才算不同,那么 \(f\) 就是子树点个数,一个 DFS 解决。
对于位置不同才算不同的情况,我们给每个点赋一个权值 \(sz_i\),表示这个点在字符串中出现的次数(就是 \(\operatorname{endpos}\) 集合大小),\(f\) 就是子树和。
那么怎么求 \(sz_i\)?我们发现,每个字符串都会使它到根节点的路径上的节点的 \(\operatorname{endpos}\) 集合大小加一。于是 \(sz_i\) 还是一个子树和,同样 DFS。
总结:对于前三道题,我们发现:SAM 上求关于字典序的问题十分方便(直接走即可),而且我们做题时也经常需要一些 SAM 上的 DP。这是 SAM 的基本应用。
- Longest Common Substring
给定两个字符串 \(s,t\),求它们的最长公共子串长度。
sol:
我们考虑求出这样一个数组:\(f_i\) 表示 \(t\) 的前 \(i\) 个字符和 \(s\) 的必须以 \(t_i\) 结尾的最长公共子串。即最长的 \(x\) 使得 \(t[i-x+1,i]\) 是 \(s\) 的子串。
对 \(s\) 建 SAM,并让 \(t\) 在上面跑。我们枚举 \(t\) 的每一个字符,并维护当前走到的节点 \(nw\) 与最长公共子串 \(l\)。假设枚举到了 \(t_i\)。
如果 \(nw\) 有 \(t_i\) 的出边,那么直接走即可,更新 \(l\)。
否则,我们像 AC 自动机一样,不停跳 \(nw\) 的父亲,直到根节点或有 \(t_i\) 的出边为止,然后走过去。可以感性理解:AC 自动机跳到的是字符串中存在了的最长的后缀,SAM 跳到的是是 \(s\) 的子串的最长的后缀。
最后的答案就是每次的 \(l\) 的最大值。
- Cyclical Quest
给定主串 \(s\) 和 \(n\) 个询问串,求每个询问串的所有循环同构在主串中出现的次数总和。
sol:
显然有暴力做法:枚举每个循环同构。但是我们发现一个性质:删去最前面的字符,在后面加上一个字符,就可以得到另一个循环同构。
于是,我们可以像上题一样,每次加一个字符,并维护当前最长公共子串。如果它的长度大于询问串长,那么就出现了一次。注意如果最长公共子串长大于询问串长,那么我们需要不停跳父亲,直到它不满足(因为要去除最前面字符的影响)。
- 封印
给定两个字符串 \(s,t\),\(q\) 次询问,每次询问 \(s[l\cdots r]\) 和 \(t\) 的最长公共子串长度。
sol:
根据上面的题,我们很容易想到对 \(t\) 建 SAM,然后同样处理出 \(f_i\) 表示最长的 \(s[i-f_i+1,i]\) 是 \(t\) 的子串。
考虑询问的是什么。很显然,就是下面这个式子:
挖掘一下她的性质,可以发现:每加一个字符时,\(f_i\) 最多加一,而且有可能清零。所以,必然有一个分界线,满足它左边都 \(i-l+1<f_i\),右边都 \(f_i<i-l+1\)。
二分出边界,再线段树查区间 \(\max\) 即可。
总结:对于上面三道题,我们发现都是和公共子串相关的内容。我们可以使用 SAM 简单求出以每一个位置结尾的最长公共子串,帮助我们解决问题。
- 广义后缀自动机
给定 \(n\) 个由小写字母组成的字符串 \(s_1,s_2,\cdots,s_n\),求本质不同的子串个数。
sol:
这题把 SAM 单串的问题扩展到了多串。我们很容易想到这样一种方法:每加完一个串,就把 \(ls\) 设为 \(1\),重新从根节点添加。
这样做,我们确实也建出了一个可以接受所有后缀的自动机,所以这种方法可以在许多题中通过。但是,这样建出的自动机不一定是点数最小的,它可能有空节点,可能在统计过程中出问题。
为什么会有空节点?还是感性理解:你前面几个串已经建好了一个 SAM,现在又加了一个串,它在沿着已有的转移边 \((p,q)\) 走时可能 \(l_p+1\neq l_q\)(\(l_p+1=l_q\) 可以判掉,因为你想要加的点已经存在了,直接用即可)。于是没有任何边会连向新建的点,而它应该记录的新信息却被全部记录在了从 \(p\) 复制出来的那个点上。于是它就成为了一个只有父亲连边的空节点。
如何避免呢?如果当前没有已有的转移边则和普通 SAM 一样。否则,我们首先加上上面的判存在的特判,然后就是上面讲的产生空节点的情况。处理很简单,我们不新建节点,把 \(ls\) 设为从 \(p\) 复制出来的那个点就行了。
- Standing Out from the Herd
给定一些字符串,请计算每个字符串中不与其他串共享的子串的数量。
sol:
建出广义 SAM。对于每一个串,我们把从它的每个前缀对应的节点到根节点的路径上都打上它的标记(每个串标记不同)。如果一个节点有多个标记,那么它就失效。
最后对于每个节点 \(x\),把它标记的那个串的答案加上 \(l_x-l_{f_x}\)。
总结:上面两题是广义 SAM 的基本应用。其实就是把单串的方法用到多串上即可。
- Paper Task
给定一个长度为 \(n\) 的括号串,问有多少种不同的合法括号子串。
sol:
考虑没有本质不同怎么做:每个括号赋权值 \(1\) 或 \(-1\),然后合法序列有两个条件:
-
序列和为 \(0\)。
-
序列所有后缀和非负。
于是对于每个右端点 \(r\),二分出满足后缀和非负的最左端点 \(l\)。然后第一个条件用线段树判一下即可。
如果有本质不同,那么如果右端点移动一位,产生的新的子串一定左端点在某个 \([1,x]\) 之间,使用 SAM 维护出来就行了。
总结:对于一些求本质不同子串个数的问题,我们可以使用 SAM 将她简化为普通的没有本质不同要求的问题,从而更好处理。
- Security
给出一个字符串 \(s\) 和一些询问,每次给定 \(l,r,t\),求字典序最小的 \(s_1\),使得 \(s_1\) 为 \(s[l\ldots r]\) 的子串,且 \(s_1\) 的字典序严格大于 \(t\)。
sol:
从后往前枚举 \(t\),假设当前枚举到了 \(x\)。如果当前 \(t[1\ldots x]\) 拼上一个大于 \(t_{x+1}\) 的字符在 \(s[l\ldots r]\) 中,那么它就是答案,否则 \(x\) 减一,继续判断。
现在主要的问题是:如何判断一个节点的字符串是否在 \(s[l\ldots r]\) 中。转化为 \(\operatorname{endpos}\) 的问题:假设串长度为 \(sz\),判断节点是否存在一个 \(\operatorname{endpos}\) 在 \([l+sz-1,r]\) 中。这可以线段树合并解决。
- Forensic Examination
给你一个串 \(s\) 以及一个字符串数组 \(t_{1\ldots m}\),\(q\) 次询问,每次问 \(s[p_l\ldots p_r]\) 在 \(T_{l\ldots r}\) 中的哪个串里的出现次数最多,并求出出现次数。
sol:
首先建出广义 SAM。对于每个询问,我们需要先找到 \(s[p_l\ldots p_r]\) 在树上的对应节点。预处理每个前缀的对应节点,然后在 SAM 上倍增跳父亲即可。
然后就是树上询问子树中出现次数最大的颜色(CF600E),线段树合并即可。
- 你的名字
给定一个字符串 \(s\),\(q\) 次询问,每次给定一个字符串 \(t\) 和 \(l,r\),求 \(t\) 有多少个本质不同的且没在 \(s[l\ldots r]\) 中出现过的子串。
sol:
我们反向考虑问题,考虑求出以每个 \(t_i\) 为结尾的与 \(s[l\ldots r]\) 的最长公共子串。
我们发现,这个东西就是 SP1811 加上了一个 \(s[l\ldots r]\) 子串的限制。只需要线段树合并求出 \(\operatorname{endpos}\),在跳的过程中加上一个判断即可。
总结:上面三道题是线段树合并维护 \(\operatorname{endpos}\) 的基础例题,这个方法十分有用。
进阶
- String Journey
给定一个字符串 \(S\),你需要从前往后选出若干个不交的子串,使得每个子串都是上一个的真子串,求最多能选出多少段。
sol:
先将串反过来,那么每次选的串都要包含上一个串。我们发现最终选的串的长度一定是 \(1,2,\ldots,k\) 的,因为如果有不符合条件的可以删去字符来使得满足条件。
考虑 DP,设 \(f_i\) 表示前 \(i\) 个字符最多能划分出多少段,且最后一段长度为 \(f_i\) 且右端点为 \(i\)。每次求可以二分答案,假设当前二分的是 \(t\),那么最后一段就是 \(S[i-t+1\ldots i]\),因为上一段比当前段长度少 \(1\),于是只有可能是 \(S[i-t\ldots i-1]\) 或 \(S[i-t+2\ldots i]\)。找到这两个串对应的节点,它的所有出现位置就是 SAM 上的子树,dfn 序后线段树维护每个位置 \(f\) 值,枚举时线段树上增加即可。
我们还可以优化:对于一个 \(f_i\),一定有一种方案是把 \(f_{i+1}\) 的每一段删去最后一个字母,所以 \(f_i\ge f_{i+1}-1\),于是就可以暴力跳 \(f_i\),时间复杂度为 \(\mathcal{O}(n\log n)\)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号