2017清北学堂(提高组精英班)集训笔记——图论
我们进入一个新的模块——图论!
emmmmm这个专题更出来可能有点慢别介意,原因是要划的图和要给代码加的注释比较多,更重要的就是。。。这几个晚上我在追剧!!我们的少年时代超级超级超级好看,剧情很燃啊!!咳咳,好吧下面回归正题。
一、图的存储:
1、邻接矩阵:
假设有n个节点,建立一个n×n的矩阵,第i号节点能到达第j号节点就将[i][j]标记为1(有权值标记为权值),
样例如下图:

1 /*无向图,无权值*/ 2 int a[MAXN][MAXN];//邻接矩阵 3 int x,y;//两座城市 4 for(int i=1;i<=n;i++) 5 { 6 for(int j=1;j<=n;j++) 7 { 8 scanf("%d%d",&x,&y);//能到达,互相标记为1 9 a[x][y]=1; 10 a[y][x]=1; 11 } 12 } 13 /*无向图,有权值*/ 14 int a[MAXN][MAXN];//邻接矩阵 15 int x,y,w;//两座城市,路径长度 16 for(int i=1;i<=n;i++) 17 { 18 for(int j=1;j<=n;j++) 19 { 20 scanf("%d%d%d",&x,&y,&w);//能到达,互相标记为权值w 21 a[x][y]=w; 22 a[y][x]=w; 23 } 24 } 25 /*有向图,无权值*/ 26 int a[MAXN][MAXN];//邻接矩阵 27 int x,y;//两座城市 28 for(int i=1;i<=n;i++) 29 { 30 for(int j=1;j<=n;j++) 31 { 32 scanf("%d%d",&x,&y);//能到达,仅仅是x到y标记为1 33 a[x][y]=1; 34 } 35 } 36 /*有向图,有权值*/ 37 int a[MAXN][MAXN];//邻接矩阵 38 int x,y,w;//两座城市,路径长度 39 for(int i=1;i<=n;i++) 40 { 41 for(int j=1;j<=n;j++) 42 { 43 scanf("%d%d%d",&x,&y,&w);//能到达,仅仅是x到y标记为权值w 44 a[x][y]=w; 45 } 46 }
邻接矩阵很方便,但是在n过大或者为稀疏图时,就会很损耗时空,不建议使用!
2.邻接表:
邻接表是一个二维容器,第一维描述某个点,第二维描述这个点所对应的边集们。
邻接表由表头point,链点构成,如下图是一个简单无向图构成的邻接表:
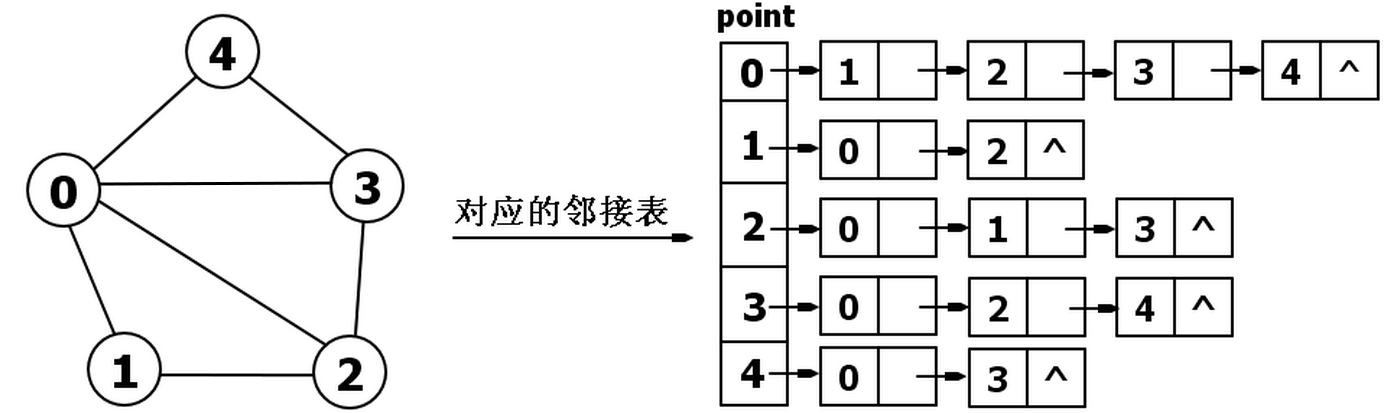
我们可以用指针来创建链表,当然,这是很复杂也很麻烦的事情,下面来介绍一种用数组模拟链表的方法:
1 //有向图邻接表存储 2 const int N=1005; 3 const int M=10050; 4 int point[N]={0};//i节点所对应链表起始位置(表头) 5 int to[M]={0}; 6 int next[M]={0};//i节点下一个所指的节点 7 int cc=0;//计数器(表示第几条边) 8 void AddEdge(int x,int y)//节点x到y 9 { 10 cc++; 11 to[cc]=y; 12 next[cc]=point[x]; 13 point[x]=cc; 14 } 15 void find(int x) 16 { 17 int now=point[x]; 18 while(now) 19 { 20 printf("%d\n",to[now]); 21 now=next[now]; 22 } 23 } 24 int main() 25 { 26 27 }
具体的过程我也不是很懂怎么描述,反正如果要加强记忆的话可以用我所给的例子模拟一下point[],to[],next[],然后再调用函数find(x)来输出x这个节点能到的点,大概就能YY到数组是怎么存储邻接表的了。
还是不理解的话,推一个blog,这里面说的和我这里给出的思路很相似:http://developer.51cto.com/art/201404/435072.htm
二、树的遍历:
1.BFS:运用队列,一开始队列中有一个点, 将一个点出队,将它的子结点全都入队。
算法会在遍历完一棵树中每一层的每个结点之后,才会转到下一层继续,在这一基础上,队列将会对算法起到很大的帮助:

1 //广度优先搜索 2 void BreadthFirstSearch(BitNode *root) 3 { 4 queue<BitNode*> nodeQueue; 5 nodeQueue.push(root);//将根节点压入队列 6 while (!nodeQueue.empty())//队列不为空,继续压入队列 7 { 8 BitNode *node = nodeQueue.front(); 9 nodeQueue.pop();//弹出根节点 10 if (node->left)//左儿子不为空 11 { 12 nodeQueue.push(node->left);//压入队列 13 } 14 if (node->right)//右儿子不为空 15 { 16 nodeQueue.push(node->right);//压入队列 17 } 18 } 19 }
2.DFS:运用栈,递归到一个点时,依次递归它的子结点。
还可以利用堆栈的先进后出的特点,现将右子树压栈,再将左子树压栈,这样左子树就位于栈顶,可以保证结点的左子树先与右子树被遍历:

1 //深度优先搜索 2 //利用栈,现将右子树压栈再将左子树压栈 3 void DepthFirstSearch(BitNode *root) 4 { 5 stack<BitNode*> nodeStack; 6 nodeStack.push(root);//将根节点压栈 7 while (!nodeStack.empty())//栈不为空,继续压栈 8 { 9 BitNode *node = nodeStack.top();//引用栈顶 10 cout << node->data << ' '; 11 nodeStack.pop();//弹出根节点 12 if (node->right)//优先遍历右子树 13 { 14 nodeStack.push(node->right); 15 } 16 if (node->left) 17 { 18 nodeStack.push(node->left); 19 } 20 } 21 }
三、无根树变成有根树:
选择一个点作为根结点, 开始遍历。
遍历到一个点时, 枚举每一条连接它和另一个点的边。 若另一个点不是它的父结点, 那就是它的子结点。 递归到子结点。
我们可以更加形象的比喻为:抓住一个点,把它拎起来构成一棵新的树。
四、并查集:
这是我学OI这么久以来觉得性价比最高的算法(简单又实用啊!!),用来处理不相交合并和查询问题。
给大家推个超超超超级易懂的blog,保证一看就懂,这里我就不再详解了:http://blog.csdn.net/dellaserss/article/details/7724401
五、最小生成树:
1.Prim算法(适用于稠密图):
算法描述:

1 #include<stdio.h>//普里姆算法 2 const int N=1050; 3 const int M=10050; 4 struct Edge//定义图类型结构体,a到b权值为c 5 { 6 int a,b,c; 7 }edge[M]; 8 int n,m;//n个点,m条边 9 bool black[N];//染黑这个点,表示这个点已经被选过了 10 int ans=0;//最小生成树权值和 11 int main() 12 { 13 int i,j,k; 14 scanf("%d%d",&n,&m); 15 for(i=1;i<=m;i++) 16 scanf("%d%d%d",&edge[i].a,&edge[i].b,&edge[i].c); 17 black[1]=1;//把第一个点染黑(从第一个点找起) 18 for(k=1;k<n;k++) 19 { 20 int mind,minz=123456789; 21 for(i=1;i<=m;i++)//开始! 22 { 23 if(black[edge[i].a]!=black[edge[i].b]&&edge[i].c<minz)//如果这个点未被找过并且权值比当前最优值还要小,更新之 24 { 25 mind=i;//记录当前最优点 26 minz=edge[i].c;//记录当前最小边权 27 } 28 } 29 /*******************************************///将这最优点归入 30 ans+=minz;//答案加上 31 black[edge[mind].a]=1;//染黑两个节点 32 black[edge[mind].b]=1; 33 /*******************************************/ 34 } 35 printf("%d\n",ans);//输出答案 36 return 0; 37 }
2.kruskal算法(适用于稀疏图):
算法描述:
克鲁斯卡尔算法从另一途径求网的最小生成树。
假设连通网N=(V,{E}),则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=(V,{∮}),图中每个顶点自成一个连通分量。
在E中选择代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边而选择下一条代价最小的边。
依次类推,直至T中所有顶点都在同一连通分量上为止。

1 #include<cstdio>//克鲁斯卡尔算法 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=1050; 6 const int M=10050; 7 struct Edge//定义图类型结构体 8 { 9 int a,b,c;//a到b的权值为c 10 }edge[M]; 11 int fa[N];//父亲数组 12 int n,m;//n个节点,m条边 13 int ans=0;//最小生成树权值和 14 bool cmp(Edge x,Edge y)//比较权值大小 15 { 16 return (x.c<y.c); 17 } 18 int getf(int x)//寻找x的最原始祖先(并查集) 19 { 20 if(fa[x]!=x) 21 fa[x]=getf(fa[x]); 22 return fa[x];//返回最原始祖先 23 } 24 int main() 25 { 26 int i,j; 27 scanf("%d%d",&n,&m); 28 for(i=1;i<=m;i++) 29 scanf("%d%d%d",&edge[i].a,&edge[i].b,&edge[i].c); 30 sort(edge+1,edge+m+1,cmp);//从小到大排序边数组 31 for(i=1;i<=n;i++) 32 fa[i]=i;//初始值,每个节点的父亲就是自己 33 for(i=1;i<=m;i++) 34 { 35 int a=edge[i].a; 36 int b=edge[i].b; 37 a=getf(a);//寻找a的最原始祖先 38 b=getf(b);//寻找b的最原始祖先 39 if(a!=b)//如果两个的最终祖先不相同(不会构成回路) 40 { 41 ans+=edge[i].c;//加入 42 fa[a]=b;//加入当前父亲的儿子们中(合并并查集) 43 } 44 } 45 printf("%d\n",ans); 46 return 0; 47 }
经典例题:繁忙的都市(Luogu 2330)
城市C是一个非常繁忙的大都市,城市中的道路十分的拥挤,于是市长决定对其中的道路进行改造。城市C的道路是这样分布的:城市中有n个交叉路口,有些交叉路口之间有道路相连,两个交叉路口之间最多有一条道路相连接。这些道路是双向的,且把所有的交叉路口直接或间接的连接起来了。每条道路都有一个分值,分值越小表示这个道路越繁忙,越需要进行改造。但是市政府的资金有限,市长希望进行改造的道路越少越好,于是他提出下面的要求:
1.改造的那些道路能够把所有的交叉路口直接或间接的连通起来。
2.在满足要求1的情况下,改造的道路尽量少。
3.在满足要求1、2的情况下,改造的那些道路中分值最大的道路分值尽量小。
任务:作为市规划局的你,应当作出最佳的决策,选择那些道路应当被修建。
这题是经典的最小瓶颈生成树问题:只用边权小于等于x的边,看看能不能构成最小生成树。
在kruskal算法中,我们已经对边从小到大排过序了,所以只要用≤x的前若干条边即可。
3.最小生成树计数问题:
题目:现在给出了一个简单无向加权图。你不满足于求出这个图的最小生成树,而希望知道这个图中有多少个不同的最小生成树。(如果两颗最小生成树中至少有一条边不同,则这两个最小生成树就是不同的)。
解法:按边权排序,先选小的,相同边权的暴力求出有几种方案,将边按照权值大小排序,将权值相同的边分到一组,统计下每组分别用了多少条边。然后对于每一组进行dfs,判断是否能够用这一组中的其他边达到相同的效果。最后把每一组的方案数相乘就是答案。
换句话说:就是不同的最小生成树方案,每种权值的边的数量是确定的,每种权值的边的作用是确定的, 排序以后先做一遍最小生成树,得出每种权值的边使用的数量x然后对于每一种权值的边搜索,得出每一种权值的边选择方案。
1 #include<cstdio> 2 #include<algorithm> 3 #define N 105 4 #define M 1005 5 #define MOD 31011 6 using namespace std; 7 struct node//定义图类型结构体 8 { 9 int a,b;//节点a,b 10 int zhi;//a到b的权值 11 }xu[M]; 12 int n,m; 13 int fa[N]; 14 int lian[N]; 15 int ans=1; 16 int cmp(struct node x,struct node y)//从小到大排序函数 17 { 18 return (x.zhi<y.zhi); 19 } 20 int getf(int x) 21 { 22 if(fa[x]!=x) 23 fa[x]=getf(fa[x]); 24 return(fa[x]); 25 } 26 int getlian(int x) 27 { 28 if(lian[x]==x) 29 return x; 30 return ( getlian(lian[x]) ); 31 } 32 int dfs(int now,int end,int last) 33 { 34 if(now==end) 35 { 36 if(last==0) 37 return 1; 38 return 0; 39 } 40 int res=dfs(now+1,end,last); 41 int s=getlian(xu[now].a); 42 int t=getlian(xu[now].b); 43 if(s!=t) 44 { 45 lian[s]=t; 46 res+=dfs(now+1,end,last-1); 47 lian[s]=s; 48 } 49 return res; 50 } 51 int main() 52 { 53 int i,j,k; 54 int s,t; 55 int now; 56 int sum=0; 57 scanf("%d%d",&n,&m); 58 for(i=1;i<=n;i++)//初始化,每个节点的父亲就是自己 59 fa[i]=i; 60 for(i=1;i<=m;i++) 61 scanf("%d%d%d",&xu[i].a,&xu[i].b,&xu[i].zhi); 62 sort(xu+1,xu+m+1,cmp);//从小到大排序边数组 63 for(i=1;i<=m;) 64 { 65 for(j=1;j<=n;j++) 66 lian[j]=j; 67 k=i; 68 while(i<=m&&xu[i].zhi==xu[k].zhi) 69 { 70 xu[i].a=getf(xu[i].a); 71 xu[i].b=getf(xu[i].b); 72 i++; 73 } 74 now=sum; 75 for(j=k;j<i;j++) 76 { 77 s=getf(xu[j].a); 78 t=getf(xu[j].b); 79 if(s!=t) 80 { 81 sum++; 82 fa[s]=t; 83 } 84 } 85 ans*=dfs(k,i,sum-now); 86 ans%=MOD;//防止溢出 87 } 88 if(sum!=n-1) 89 ans=0; 90 printf("%d\n",ans); 91 return 0; 92 }
六、最短路径:
1.Floyd算法(插点法):
通过一个图的权值矩阵求出它的每两点间的最短路径(多源最短路)。
算法描述:
一个十分暴力又经典的DP,假设i到j的路径有两种状态:
①i和j直接有路径相连:![]()
②i和j间接联通,中间有k号节点联通:![]()
假设dis[i][j]表示从i到j的最短路径,对于存在的每个节点k,我们检查一遍dis[i][k]+dis[k][j]。
1 //Floyd算法,时间复杂度:O(n^3) 2 int dis[MAXN][MAXN]; 3 for(k=1;k<=n;k++)//枚举 4 { 5 for(i=1;i<=n;i++) 6 { 7 for(j=1;j<=n;j++) 8 { 9 dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);//DP 10 } 11 } 12 }
2.Dijkstra算法(无向图,无负权边):
算法描述:
多源最短路!
a.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
啊~上面的的乱七八糟的概念太难懂了,还是举个例子吧!如下图!

我们假设1号节点为原点。
第一轮,我们可以算出2,3,4,5,6号节点到原点1的距离为[7,9,∞,∞,14],∞表示无穷大(节点间无法直接连通),取其中最小的7,就确定了1->1的最短路径为0,1->2的最短路径为7,同时取最短路径最小的2节点为下一轮的前驱节点。
第二轮,取2节点为前驱节点,按照 前驱节点到原点的最短距离 + 新节点到前驱节点的距离 来计算新的最短距离,可以得到3,4,5,6号节点到原点1的距离为[17,22,∞,∞](新节点必须经过2号节点回到原点),这时候需要将新结果和上一轮计算的结果比较,3号节点:17>9,最短路径仍然为9;4号节点:22<∞,更新4号节点的最短路径为22,;5号节点:仍然不变为∞;6号节点:14<∞,更新6号节点的最短路径为14。得到本轮的最短距离为[9,22,∞,14],1->3的最短路径为9,同时取最短路径最小的3节点为下一轮的前驱节点。
第三轮:同理上,以3号节点为前驱节点,可以得到4,5,6号节点到原点1的距离为[20,∞,11],根据最短路径原则,和上一轮最短距离比较,刷新为[20,∞,11],1->3->6的最短路径为11,同时取最短路径最小的6节点为下一轮的前驱节点。
第四轮:同理,得到4,5号节点最短距离为[20,20],这两个值相等,运算结束,到达这两个点的最短距离都是20,如果这两个值不相等,还要进行第五轮运算!
1 #include<cstdio> 2 #include<cstring> 3 const int N=100500; 4 const int M=200500; 5 int point[N]={0},to[M]={0},next[M]={0},len[M]={0},cc=0; 6 int dis[N];//最短路长度,dis[i]表示第i号点到源点(1号点)的最短距离 7 bool ever[N];//当前节点最短路有没有确定 8 int n,m; 9 void AddEdge(int x,int y,int z)//添加新的边和节点:x到y边长z 10 { 11 cc++; 12 next[cc]=point[x]; 13 point[x]=cc; 14 to[cc]=y; 15 len[cc]=z;//len记录x到y的边长 16 } 17 int main() 18 { 19 int i,j,k; 20 scanf("%d%d",&n,&m); 21 for(i=1;i<=m;i++) 22 { 23 int a,b,c; 24 scanf("%d%d%d",&a,&b,&c); 25 AddEdge(a,b,c);//无向图,要加两遍 26 AddEdge(b,a,c); 27 } 28 memset(dis,0x3f,sizeof dis);//用极大值来初始化 29 dis[1]=0;//1号节点到自己最短距离为0 30 for(k=1;k<=m;k++) 31 { 32 int minp,minz=123456789; 33 for(i=1;i<=n;i++) 34 { 35 if(!ever[i]) 36 { 37 if(dis[i]<minz) 38 { 39 minz=dis[i]; 40 minp=i; 41 } 42 } 43 } 44 ever[minp]=1; 45 int now=point[minp]; 46 while(now) 47 { 48 int tox=to[now]; 49 if(dis[tox]>dis[minp]+len[now]) 50 dis[tox]=dis[minp]+len[now]; 51 now=next[now]; 52 } 53 } 54 for(i=1;i<=n;i++) 55 printf("%d\n",dis[i]); 56 return 0; 57 }
3.SPFA算法(有负权边,无负圈,能检测负圈但不能输出):
多源最短路!
SPFA和Dijkstra极为相似,只是加了个队列优化来检测负圈和负权边。
算法描述:
建立一个队列,初始时队列里只有起始点,再建立一个表格记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到他本身的路径赋为0)。然后执行松弛操作,用队列里有的点作为起始点去刷新到所有点的最短路,如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。
判断有无负环:
如果某个点进入队列的次数超过N次则存在负环(SPFA无法处理带负环的图)
1 #include<cstdio> 2 #include<cstring> 3 const int N=100500; 4 const int M=200500; 5 int point[N]={0},to[M]={0},next[M]={0},len[M]={0},cc=0; 6 int dis[N];//最短路长度 7 int queue[N],top,tail;//双向队列queue,队头,队尾 8 bool in[N];//记录这个点在不在队列中,1表示在,0表示不在 9 int n,m; //n个节点,m条边 10 void AddEdge(int x,int y,int z)//x到y边长为z 11 { 12 cc++; 13 next[cc]=point[x]; 14 point[x]=cc; 15 to[cc]=y; 16 len[cc]=z; 17 } 18 int main() 19 { 20 int i,j; 21 scanf("%d%d",&n,&m); 22 for(i=1;i<=m;i++) 23 { 24 int a,b,c; 25 scanf("%d%d%d",&a,&b,&c); 26 AddEdge(a,b,c);//因为是双向队列,左边加一次,右边加一次 27 AddEdge(b,a,c); 28 } 29 memset(dis,0x3f,sizeof dis);//用极大值来初始化 30 dis[1]=0;//1号节点到自己最短距离为0 31 top=0;tail=1;queue[1]=1;in[1]=1;//初始化,只有原点加入 32 while(top!=tail) 33 { 34 top++; 35 top%=N; 36 int now=queue[top]; 37 in[now]=0; 38 int ed=point[now]; 39 while(ed) 40 { 41 int tox=to[ed]; 42 if(dis[tox]>dis[now]+len[ed]) 43 { 44 dis[tox]=dis[now]+len[ed]; 45 if(!in[tox]) 46 { 47 tail++; 48 tail%=N; 49 queue[tail]=tox; 50 in[tox]=1; 51 } 52 } 53 ed=next[ed]; 54 } 55 } 56 for(i=1;i<=n;i++) 57 printf("%d\n",dis[i]); 58 return 0; 59 }
4.Bellman Ford算法(有负权边,可能有负圈,能检测负圈并输出):
单源最短路!
算法描述:
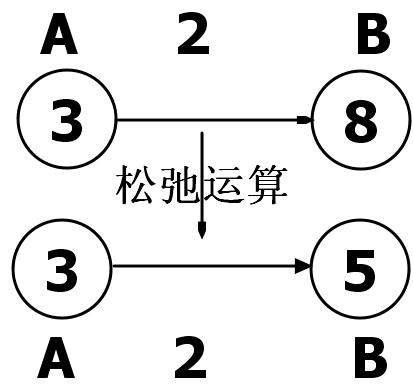

松弛操作后,变为7,7>6,这样就不修改(Bellman Frod算法的高妙之处就在这),保留原来的最短路径就OK,代码实现起来非常简单。
1 int n,m;//n个点,m条边 2 struct Edge//定义图类型结构体 3 { 4 int a,b,c;//a到b长度为c 5 }edge[]; 6 int dis[]; 7 memset(dis,0x3f,sizeof dis); 8 dis[1]=0; 9 for(int i=1;i<n;i++) 10 { 11 for(int j=1;j<=m;j++) 12 { 13 if(dis[edge[j].b]>dis[edge[j].a]+edge[j].c) 14 { 15 dis[edge[j].b]=dis[edge[j].a]+edge[j].c; 16 } 17 } 18 }
5.A*算法:
这玩意儿我是没看懂,等以后我看懂了再更吧(无奈脸)~
七、拓扑排序:
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。
打个比喻:我们要做好一盘菜名字叫做红烧茄子,那么第一步得买茄子和配料,第二步就是要洗茄子,第三步就是要开始倒油进锅里啊什么七七八八的,第四步…,你不可能先洗茄子再买茄子和配料,这样的一些事件必须是按照顺序进行的,这些依次进行的事件就构成了一个拓扑序列。
算法描述:
我们需要一个栈或者队列,两者都可以无所谓,只是找个容器把入度为0的元素维护起来而已。
①从有向图中选择一个入度为0(无前驱)的顶点,输出它。
②从网中删去该节点,并且删去从该节点出发的所有有向边。
③重复以上两步,直到剩余的网中不再存在没有前驱的节点为止。
具体操作过程如下:
若栈非空,则在栈中弹出一个元素,然后枚举这个点能到的每一个点将它的入度-1(删去一条边),如果入度=0,则压入栈中。
如果没有输出所有的顶点,则有向图中一定存在环
1 //拓扑排序,时间复杂度:O(n+m) 2 #include<cstdio> 3 #include<cstring> 4 const int N=100500; 5 const int M=200500; 6 int point[N]={0},to[M]={0},next[M]={0},cc=0; 7 int xu[N]={0};//栈,初始值为空,xu[0]表示栈的大小 8 int in[N]={0};//入度,a可以到达b,in[b]++ 9 int ans[N]={0};//ans[0]整个拓扑序列的大小 10 int n,m; 11 void AddEdge(int x,int y)//邻接表a到b 12 { 13 cc++; 14 next[cc]=point[x]; 15 point[x]=cc; 16 to[cc]=y; 17 } 18 int main() 19 { 20 int i,j; 21 scanf("%d%d",&n,&m); 22 for(i=1;i<=m;i++) 23 { 24 int a,b; 25 scanf("%d%d",&a,&b); 26 in[b]++;//统计每个节点的入度 27 AddEdge(a,b); 28 } 29 for(i=1;i<=n;i++) 30 { 31 if(in[i]==0)//这个节点入度为0,压入栈 32 xu[++xu[0]]=i; 33 } 34 while(xu[0]) 35 { 36 int now=xu[xu[0]];//出栈 37 xu[0]--; 38 ans[++ans[0]]=now; 39 int ed=point[now]; 40 while(ed) 41 { 42 int tox=to[ed]; 43 in[tox]--; 44 if(!in[tox]) 45 xu[++xu[0]]=tox; 46 ed=next[ed];//找下一个相邻节点 47 } 48 } 49 if(ans[0]<n)//有向图中一定存在环,无结果 50 printf("no solution"); 51 else 52 { 53 for(i=1;i<=n;i++) 54 printf("%d ",ans[i]); 55 } 56 return 0; 57 }
八、联通分量:
强连通:有向图中,从a能到b并且从b可以到a,那么a和b强连通。
强连通图:有向图中,任意一对点都满足强连通,则这个图被称为强连通图。
强联通分量:有向图中的极大强连通子图,就是强连通分量。
一般用Tarjan算法求有向图强连通分量:
推一个蛮容易理解的blog:http://www.cnblogs.com/uncle-lu/p/5876729.html
九、欧拉路径与哈密顿路径:
1.欧拉路径:从某点出发一笔画遍历每一条边形成的路径。
欧拉回路:在欧拉路径的基础上回到起点的路径(从起点出发一笔画遍历每一条边)。
欧拉路径存在:
无向图:当且仅当该图所有顶点的度数为偶数 或者 除了两个度数为奇数外其余的全是偶数。
有向图:当且仅当该图所有顶点 出度=入度 或者 一个顶点 出度=入度+1,另一个顶点 入度=出度+1,其他顶点 出度=入度
欧拉回路存在:
无向图:每个顶点的度数都是偶数,则存在欧拉回路。
有向图:每个顶点的入度都等于出度,则存在欧拉回路。
求欧拉路径/欧拉回路算法常常用Fleury算法:
再推一个蛮容易理解的blog:http://www.cnblogs.com/Lyush/archive/2013/04/22/3036659.html
2.哈密顿路径:每个点恰好经过一次的路径是哈密顿路径。
哈密顿回路:起点与终点之间有边相连的哈密顿路径是哈密顿回路。
最近发现一些网站盗用我的blog,这实在不能忍(™把关于我的名字什么的全部删去只保留文本啥意思。。)!!希望各位转载引用时请注明出处,谢谢配合噢~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号