信贷场景下深入理解WOE (转)
一、woe是什么？
WOE，全称是“Weight of Evidence”，翻译过来就是证据权重,是对于字符型变量的某个值或者是连续变量的某个分段下的好坏客户的比例的对数。实际的应用会将原始变量对应的数据替换为应用WOE公式后的数据，也称作WOE编码或者WOE化。
WOE编码需要首先将这个变量分组处也就是分箱。一般选择使用均匀分箱，离散型数据分箱个数就是该数据的数据类别个数，连续型数据一般会使用6组，尽可能均分。对某一变量分完组后，假设第i组下的数据的WOE的计算公式为：
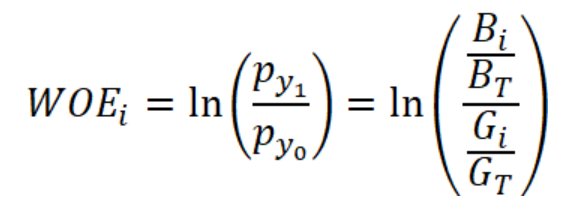
这个第i组的WOE，其中Bi表示这一组的风险客户，BT表示这一样本总的风险客户，Gi表示这一组的正常客户，也就是无风险客户，GT表示这样本总的正常客户。所以WOE就是将风险客户在所有风险客户的比例和正常客户在所有正常客户的比例，这两者做比，衡量的是两者的差异，再取对数，两者差异越大，对风险客户区分越明显。我们也如果对这个公式做个分子分母的变换，就可以得到：
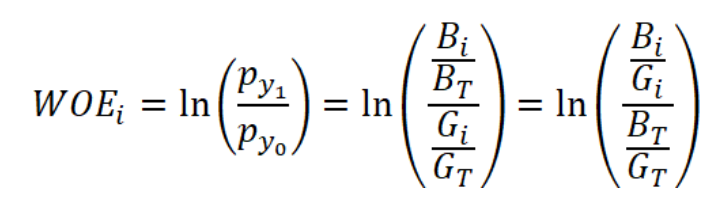
变换后我们也可以这样去理解WOE的含义，它表示的是当前这个组中风险的客户和正常客户的比值，和总体数据集中对应的这个比值的差异。这个差异是用这两个比值的比值，再取对数来表示的。
二、使用示例
以借贷场景下的信用评分卡的建模场景为例：X是客户样本字段，Y表示客户逾期与否，其中Y=1代表逾期，Y=0代表未逾期。我们希望能用客户已知的信息来预测客户借款后发生逾期的概率，以此来决定是否放贷。
下面我们拿Age(年龄)这个变量来计算woe值。
1.首先对每个level分层统计：
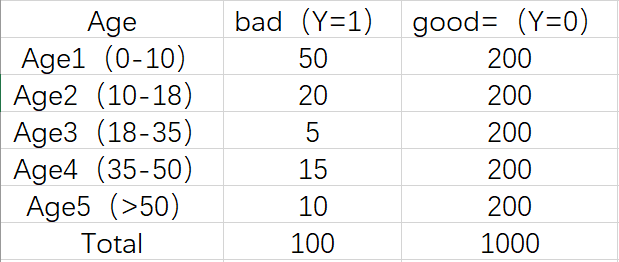
2.计算各分层的好坏客户占比：
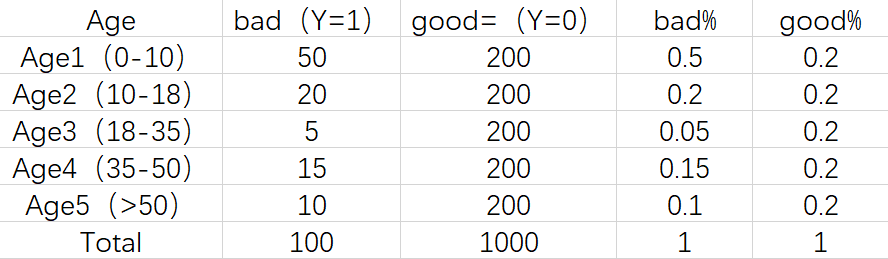
3.最后通过好坏客户占比完成WOE化：
统计上看WOE的本质为正常客户分布与不良客户分布的对数似然比。WOE越大，差异越大，这个分组里的样本为风险客户的可能性就越大，WOE越小，差异越小，这个分组里的样本中含有的风险客户的可能性就越小。
WOE反应的是逻辑回归中的比例，但WOE只考虑了对风险客户的区分的能力，但没有考虑能区分的申请人有多少。所以这里引出一个IV值的概念，IV值就考虑了这个变量能够区分风险客户的数量。
三、WOE使用场景
在对变量处理的可以WOE化也可以不做WOE化，但是在小额贷款的风控模型中，如果对变量离散化后不做WOE化处理，一般会将离散变量或者一些类别变量做成哑变量。做成哑变量而不是直接用离散化后的变量是因为离散化之后的变量很难知道各个组之间的数量关系。
比如组别分成三组，也许可以直接赋1、2、3的数量关系，但是这个数量关系仅仅表示顺序，他们之间实质性的数值间隔你是不知道的。一个特征变量的每个类别都对应一个WOE值。比如例子引用中的年龄变量划分了3个变量，对应的有3个WOE值。
所以在变量离散化后不能直接使用，但是WOE化之后就可以直接使用，是因为WOE化之后，组与组之间数值未知的情况就解决了。如果参考逻辑回归模型，会发现WOE和逻辑回归是公式是类似的，有很紧密的关系。
四、WOE的好处
-
解释性强，前文所说的变量做成哑变量，实际上就是将变量拆开了，数量关系仅仅表示数据，无法表示数量关系。
-
可以观察出变量的分布情况，选择符合实际情况分布的数据。
-
WOE化后的变量值是有正负之分的，也就能从数据上看出来哪些是正向的，哪些的负向的。WOE值的大小就是这种影响的程度。
-
原始指标数据中可能蕴含着某些非线性的信息，如果没有对变量进行WOE化，数据直接使用，会导致这些非线性的信息无法表达，从而降低准确性。
