线性代数核心概念

一、齐次线性方程

常数项全为0的线性方程称为齐次线性方程，也就是没有常数项。

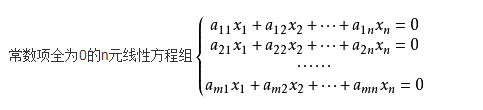
性质：

1.齐次线性方程组的系数矩阵秩r(A)=n，方程组有唯一零解。

2.齐次线性方程组的系数矩阵秩r(A)<n,方程组有无数多解。

3. n元齐次线性方程组有非零解的充要条件是其系数行列式为零，此时系数矩阵为奇异矩阵，奇异矩阵必不满秩，满秩就只有唯一零解。

4.齐次线性方程组的两个解的和仍是齐次线性方程组的一组解。

5.齐次线性方程组的解的k倍仍然是齐次线性方程组的解。

 

二、可逆矩阵与奇异矩阵

如果A的可逆矩阵A⁻¹存在，则A称为非奇异矩阵，此时矩阵A满秩，且|A|≠0。

如果A的可逆矩阵不存在，则称为A为奇异矩阵，此时A不满秩，|A|=0。

所以根据|A|是否等于0，就可以判断矩阵A是否是奇异矩阵。

注意判断是否为奇异矩阵的前提必须为方阵。

 

记忆：

一个矩阵非奇异当且仅当它的行列式不为零。 

 

一个矩阵非奇异当且仅当它代表的线性变换是个自同构。 

 

一个矩阵半正定当且仅当它的每个特征值大于或等于零。 

 

一个矩阵正定当且仅当它的每个特征值都大于零。

 

一个矩阵非奇异当且仅当它的秩为n

 

三、特征值与特征向量

 

1）公式定义

一个矩阵可以有多个特征值和与其对应的特征向量。

 

2）几何含义

对于给定矩阵A，寻找一个常数λ（可以为复数）和非零向量x，使得向量x被矩阵A作用后所得的向量Ax与原向量x平行，并且满足Ax=λx。

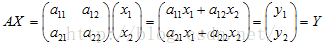
在几何上的变换如下：

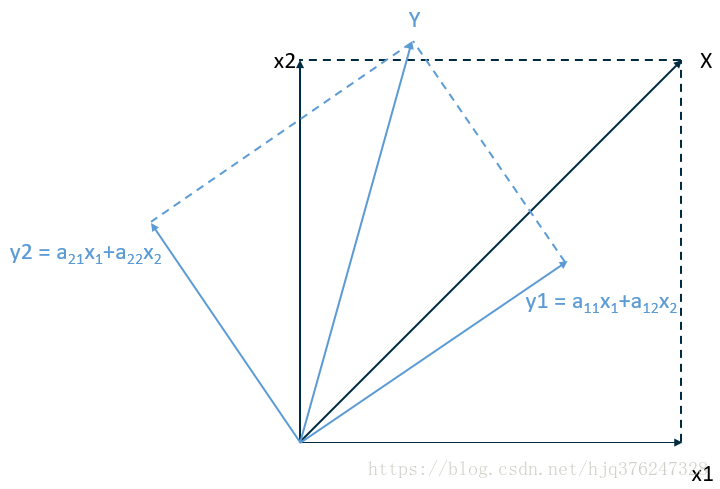
然后再去理解特征值和特征向量就好理解了：

所以，确定了特征值之后，向量x的变换为：

引用《线性代数的几何意义》的描述：“矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中，原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。”

 

四、其它知识点

1）标准正交基

在n维欧式空间中，由n个单位向量组成的正交向量组称为标准正交基

比如3维欧式空间中，

(1,0,0)、(0,1,0)、(0,0,1)是一个正交向量组，因为他们俩俩向量正交

(1,0,0)、(0,1,0)、(0,0,1)是一个正交基，因为此正交向量组由n个非零向量组成

(1,0,0)、(0,1,0)、(0,0,1)是一个标准正交基，因为每个向量都是单位向量

2）正交矩阵

如果一个矩阵是正交矩阵，则满足如下条件：

1）是一个方阵

2) A的转置矩阵也是正交矩阵

3)  （E为单位矩阵）

4) A的各行是单位向量且两两正交，也就是都是标准正交基。

5) A的各列是单位向量且两两正交

6) (Ax,Ay)=(x,y) x,y∈R

7) |A| = 1或-1

8)  ，A的转置矩阵等于A的逆矩阵