协方差与相关系数

一、协方差

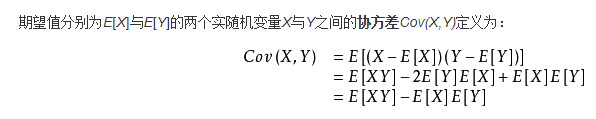
公式上理解：如果有X,Y两个变量，每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积，再对这每时刻的乘积求和并求出均值(准确说是期望，可以暂按均值方便理解)。

通俗理解：协方差反映的是两个变量是否是同向变化，你增大我也增大，则是正相关，数值为正；如果你增大我变小，则是反向变化，负相关，为负值。当随机变量X与Y独立时候，E[XY]=E[X]E[Y]，所以如果两个随机变量相互独立则其协方差COV(X,Y)=0。

深入理解：由公式可知，协方差反映的是各自值与均值之差再乘积的平均值，分几个情况讨论

1）X与Y都在同向增大，但是X的一部分值是小于均值的，而Y的对应部分正好是大于均值的，这个时候看起来乘积为负值了，但其实因为还要计算后面的部分数值的乘积，最后再相加求均值。所有如果后面有正向值了，就会相互抵消了，最终还是要看正负项的次数占比，乘积为正的部分越多，说明同向变化的次数越多，正值就越多，最后的协方差数值就越大。

 2）如果X与Y都在增大，但是X都在均值下面，Y都在均值上面，这样每个乘积都为负值，最后cov数值也为负值，怎么办？答案是这种情况不可能存在，没有这样的均值。

协方差性质：

随机变量相互独立，则协方差必为0；协方差为0，随机变量不一定相互独立，例如如果参考上述所分析的，正负值正好相加为0，因为你正值越多说明相关性越大，这个时候抵消了为0，说明两者不相关，但是不一定独立。

不相关指的是，若X和Y不相关，则仅仅是不存在线性关系，可能存在其他关系，如  ，X和Y不独立。因此，“不相关”是一个比“独立”要弱的概念

 二、相关系数

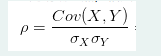
就是X,Y的协方差除以X的标准差和Y的标准差，其范围为[-1,1],

其实相关系数也可以看成协方差：一种剔除了两个变量量纲影响、标准化后的特殊协方差。

性质如下：

1)也可以反映两个变量变化时是同向还是反向，如果同向变化就为正，反向变化就为负。

2)由于它是标准化后的协方差，因此更重要的特性来了：它消除了两个变量变化幅度的影响，而只是单纯反应两个变量每单位变化时的相似程度。

3）它是一个可以表征X 和Y 之间线性关系紧密程度的量。当较大时，通常说X 和Y相关程度较好；当较小时，通常说X 和Y相关程度较差；当X和Y不相关，通常认为X和Y之间不存在线性关系，但并不能排除X和Y之间可能存在其他关系。

4）X与Y独立，则相关系数为0；相关性系数=0，表示不相关，不一定独立。

如何消除量纲呢？

如果X得取值范围从[1,100]变到[0,1]之间，Y值始终在[1,100] 之间，如果X对应的两种情况其变化趋势与Y始终一致，但是算出来的协方差可能相差几百倍，这就是因为量纲不同导致的。加入了标准差后，量纲就消除了，因为你数值波动越大，代表偏离均值越远，标准差就越大，这点跟协方差计算一致，所以两两相除抵消了。

 

参考文献：blog.sina.com.cn/s/blog_6aa3b1010102xkp5.html