基于分治的查找算法
-
顺序统计量(Order Statistic)
在一个由n个元素组成的集合中,第 i 个顺序统计量(
Order Statistic),是该集合中中第i小的元素。
例如:
最小值是第一个顺序统计量(i = 1),最大值是第n个顺序统计量,一个中位数就是其所在集合的"中点元素。"
当n为奇数时中位数在,而当n为偶数时,存在两个中位数,分别是
(下中位数) 和
(上中位数)
-
我们可以将问题抽象为从由
n个不同元素组成的集合中选择第i个顺序统计量, 由此我们定义选择问题如下:Input:一个包含n个不同元素的集合A和一个数i(![]() )
)
Output:元素x(![]() ),它恰大于
),它恰大于A中其他的i-1个元素
-
最大值和最小值
在n个元素的集合中,确定一个最值需要
n-1次比较,其查找的伪代码如下:
Minmum(A)
1. min = A[i]
2. for i <- 2 to length[A]
3. do if A[i] < min
4. then min = A[i]
5. return min
最大值的查找方法同理可得,为了确定最值,我们至少需要做
n-1次比较,从执行的次数来看,算法Minmum是最优的。
-
同时找出最大值和最小值
面对这个问题我们可以先分别找出最大值和最小值,然后问题就能得到解决,每一次找最值时需要
n-1次比较,那么总共的比较次数为2n-2次,但事实上至多需要次就能解决问题。
算法描述:
一开始从数据集合A中一次取出两个值,比较大小后将较小值放入Min将较大值放入Max,然后在剩下的数据集合中取两个数比较之后将较小值与Min相比,将较大值与Max相比,重复这个过程直至数据集合中的数据为空 (代码实现getMin&MAx)
-
线性时间做选择
一般的选择问题要比找最大值和最小值要难,一般来说需要在一个集合中查找第i个值,我们可以对其排序,然后输出数组中第i-1的值即可,如果我们使用基于决策树的排序算法去处理集合时,那么最优情况下时间复杂度为O(nlgn),如果利用CountingSort的话我们也可以在线性时间内解决这个问题,然而我们需要额外的空间来完成排序过程,有没有一种方法可以在不开辟新的空间下在线性时间内解决这个问题呢?答案是Randomized-Select
伪代码:
Randomized-Select(A,p,r,i)
1.if p == r
2. then return A[p]
3.q <- Random-Partition(A,p,r)
4.k <- q-p+1
5.if i=k
6. then return A[q]
7.elseif i < k
8.then return Randomized-Select(A,p,q - 1,i)
9.else return Randomized-Select(A,q+1,r,i-k)
算法描述:
要明白这个算法你需要先理解快速排序的随机划分过程(详情可以看我这一篇博客Analysis of QuickSort),但是和快速排序不同的是快速排序需要递归的处理数组的两边,而Randomized-Select只需要处理划分的一边,那么这一差异就体现出来了:快速排序的期望运行时间是O(nlgn),而Randomized-Select期望运行时间为O(n)
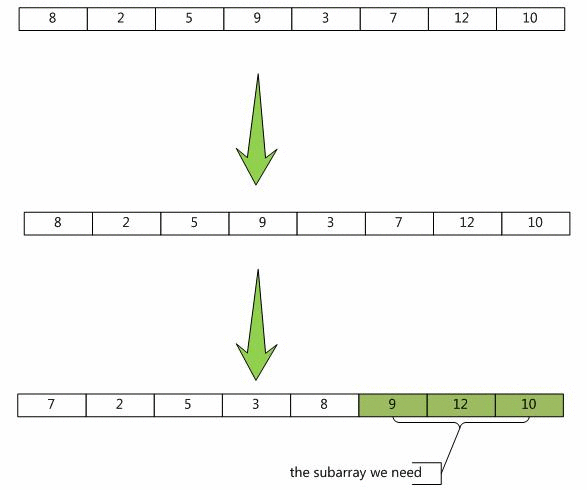
我们从数组A中需要找到第6小的数,在在第一次的划分中我们得到的数为第五个数(8),所以我们需要在它的右边部分再划分,这时由于pivot(8)为第5小的数,我们在右边部分需要查找的数应当去掉左边数组的个数,即我们需要在右边部分查找第1小的数。
-
Randomized-Select code
-
Summary
Randomized-Select的最坏情况下的运行时间为Theta(n^2),因为在划分时我们可能极不走运,总是按余下元素的最大划分,每次划分需要Theta(n),的时间,但是该算法的平均性能较好,因为它是随机化的,所以没有哪一种特别的输入会导致其最坏的情况发生,所以任何顺序统计量(特别是中位数)都可以在线性时间内得到。

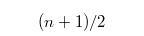 ,而当n为偶数时,存在两个中位数,分别是
,而当n为偶数时,存在两个中位数,分别是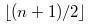 (下中位数) 和
(下中位数) 和 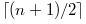 (上中位数)
(上中位数)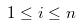 )
) ),它恰大于
),它恰大于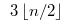 次就能解决问题。
次就能解决问题。
 浙公网安备 33010602011771号
浙公网安备 33010602011771号