2025国庆Day3
模拟赛
T1
对每个ai开个桶分别算答案即可
注意long long
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int a[1000005],mm[1000005],sum[1000005];
signed main()
{
freopen("type.in", "r", stdin);
freopen("type.out", "w", stdout);
int n=read();
for(int i=1;i<=n;i++) a[i]=read();
int m=read();
while(m--){
int p=read();
sum[1]++;
sum[p+1]--;
}
sum[1]++;
sum[n+1]--;
for(int i=1;i<=n;i++) sum[i]+=sum[i-1];
for(int i=1;i<=n;i++){
mm[a[i]]+=sum[i];
}
int ans=0;
for(int i=1;i<=n;i++){
ans^=(mm[i]*i);
}
cout<<ans<<'\n';
return 0;
}
T2
维护m个指针
倒着枚举l
p1~pm维护第i个字符已匹配的下标
每次匹配修改一个前缀
复杂度O(n)
另外可考虑:

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int s[1000005],t[1000005],p[1000005],tt[1000005],ss[1000005];
signed main()
{
freopen("jasmine.in", "r", stdin);
freopen("jasmine.out", "w", stdout);
int T=read();
while(T--){
int n=read(),m=read();
for(int i=1;i<=m;i++){
p[i]=1000000000;
}
for(int i=1;i<=n;i++) ss[i]=0;
for(int i=1;i<=n;i++){
s[i]=read();
if(s[i]<=1000000) tt[s[i]]=0;
}
for(int i=1;i<=m;i++){
t[i]=read();
}
for(int i=1;i<=n;i++){
if(s[i]>1000000) continue;
ss[i]=tt[s[i]];
tt[s[i]]=i;
}
int minn=1000000000,minl=0,minr=0;
for(int i=n;i;i--){
int l=i;
int f=0;
for(int j=1;j<=m;j++){
// cout<<f<<'\n';
if(f) break;
f=1;
while(1){
int nw=tt[t[j]];
if(p[j]!=1000000000) nw=ss[p[j]];
// cout<<nw<<'\n';
if(l<=nw){
f=0;
p[j]=nw;
}
else break;
}
l=p[j]+1;
// cout<<l<<'\n';
}
if(p[m]<=n&&p[m]-i+1<=minn){
minn=p[m]-i+1;
minl=i;
minr=p[m];
}
}
if(minn==1000000000) cout<<-1<<'\n';
else cout<<minl<<' '<<minr<<'\n';
}
return 0;
}
T3
设dpi,j表示i子树内钦定返祖j次的方案数
将相邻向北的点对连边,形成若干条链
合并子树时方案数
然后新加一个点,这个点相当于加入到任意一条链中,或者新增一条链
最后把钦定变成恰好,容斥一下
容斥大概如下
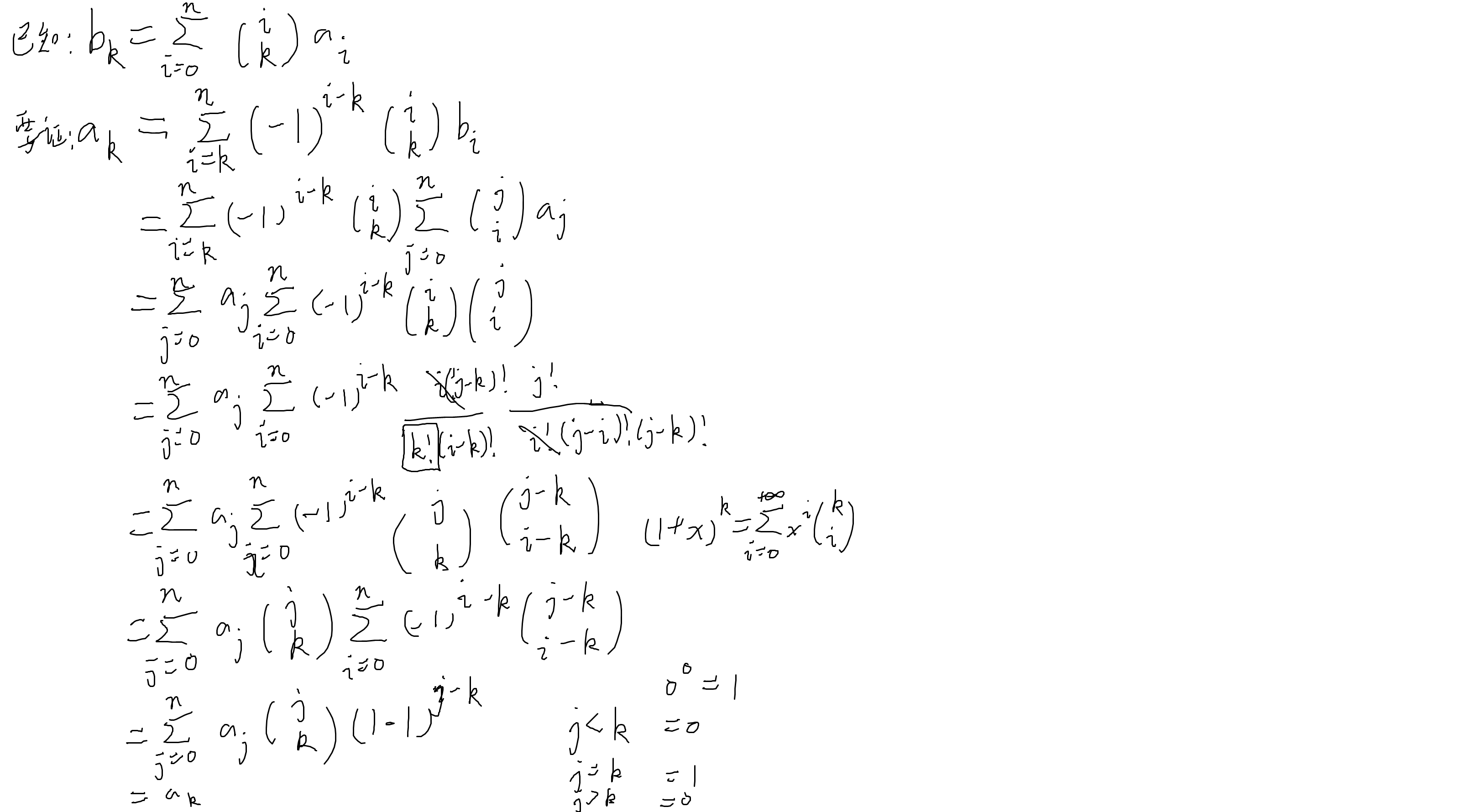
牛逼的容斥笔记
T4
牛逼的题
先考虑k=2

挖掘性质





DP
CF392B
fi,x,y表示前i个盘,从x到y的代价
容易转移
P2331
dpi,j,0~4表示第i行,选了j个矩阵
这一行的两个数{
-
没有元素被选择
-
第一列的元素在子矩阵中
-
第二列的元素在子矩阵中
-
两列元素在同一个子矩阵中
-
两列元素在不同子矩阵中
}
分别转移即可
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int dp[105][105][5];
signed main()
{
//freopen("filename.in", "r", stdin);
//freopen("filename.out", "w", stdout);
int n=read(),m=read(),k=read();
memset(dp,-0x3f,sizeof(dp));
for(int i=0;i<=n;i++){
for(int j=0;j<=k;j++) dp[i][j][0]=0;
}
if(m==1){
for(int i=1;i<=n;i++){
int a=read();
for(int j=1;j<=k;j++){
dp[i][j][0]=max(dp[i-1][j][0],dp[i-1][j][1]);
dp[i][j][1]=max(dp[i-1][j-1][0],dp[i-1][j][1])+a;
}
}
cout<<max(dp[n][k][0],dp[n][k][1])<<'\n';
}
else{
for(int i=1;i<=n;i++){
int a=read(),aa=read();
for(int j=1;j<=k;j++){
dp[i][j][0]=max(max(dp[i-1][j][0],dp[i-1][j][1]),max(dp[i-1][j][2],max(dp[i-1][j][3],dp[i-1][j][4])));
dp[i][j][1]=max(max(dp[i-1][j-1][0],dp[i-1][j][1]),max(dp[i-1][j-1][2],max(dp[i-1][j][3],dp[i-1][j-1][4])))+a;
dp[i][j][2]=max(max(dp[i-1][j-1][0],dp[i-1][j-1][1]),max(dp[i-1][j][2],max(dp[i-1][j][3],dp[i-1][j-1][4])))+aa;
dp[i][j][3]=max(max(dp[i-1][j-1][2],dp[i-1][j-1][1]),dp[i-1][j][3])+a+aa;
if(i>1) dp[i][j][3]=max(dp[i][j][3],dp[i-1][j-2][4]+a+aa);
dp[i][j][4]=max(max(dp[i-1][j-1][0],dp[i-1][j-1][1]),max(dp[i-1][j-1][2],max(dp[i-1][j-1][3],dp[i-1][j][4])))+a+aa;
}
}
cout<<max(max(dp[n][k][0],dp[n][k][1]),max(dp[n][k][2],max(dp[n][k][3],dp[n][k][4])))<<'\n';
}
return 0;
}
CF607B
fi,j表示消除[i,j]的最小代价
经典区间DP
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int dp[505][505],a[505];
signed main()
{
//freopen("filename.in", "r", stdin);
//freopen("filename.out", "w", stdout);
int n=read();
memset(dp,0x3f,sizeof(dp));
for(int i=1;i<=n;i++){
a[i]=read();
dp[i][i]=1;
if(i>1){
if(a[i]==a[i-1]) dp[i-1][i]=1;
else dp[i-1][i]=2;
}
}
for(int l=3;l<=n;l++){
for(int ll=1;ll<=n;ll++){
int r=ll+l-1;
// if(l<=2) cout<<ll<<' '<<r<<' '<<dp[ll][r]<<'\n';
if(r>n) break;
for(int k=ll;k<r;k++){
dp[ll][r]=min(dp[ll][r],dp[ll][k]+dp[k+1][r]);
}
if(a[ll]==a[r]) dp[ll][r]=min(dp[ll][r],dp[ll+1][r-1]);
}
}
cout<<dp[1][n]<<'\n';
return 0;
}
CF571B
相当于要求选择k条链
求出k条链最大值减最小值最小能是多少
容易看出每条链不交

CF703E
b为k的倍数当且仅当gcd(b,k)=k
fi,j表示前i个数gcd=j的最小元素和
而gcd(Bb,k)=gcd(b,k)gcd(b,k/gcd(B,k))
P1169
对(i+j)奇数的点取反
变成颜色全相同的最大子矩阵/正方形
子矩阵就对每个点求出往上最大延伸长度
据此算出往左往右第一个比他小的位置
计算答案
正方形就设fi,j表示以i,j左上角最大边长
若si,j=i-1,j=i,j-1=i-1,j-1
则fi,j=max(f+1)
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int a[2005][2005],dp[2005][2005],h[2005][2005],l[2005][2005],r[2005][2005];
signed main()
{
//freopen("filename.in", "r", stdin);
//freopen("filename.out", "w", stdout);
int n=read(),m=read();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
a[i][j]=read();
if((i+j)%2==0){
if(a[i][j]) a[i][j]=0;
else a[i][j]=1;
}
h[i][j]=dp[i][j]=1;
l[i][j]=r[i][j]=j;
}
}
int ans=1;
for(int i=n-1;i;i--){
for(int j=m-1;j;j--){
if(a[i][j]==a[i+1][j]&&a[i][j]==a[i][j+1]&&a[i][j]==a[i+1][j+1]){
dp[i][j]=max(min(dp[i+1][j],min(dp[i][j+1],dp[i+1][j+1]))+1,dp[i][j]);
// cout<<i<<' '<<j<<'\n';
// cout<<dp[i][j]<<'\n';
// cout<<a[i][j]<<' '<<a[i+1][j]<<' '<<a[i][j+1]<<' '<<a[i+1][j+1]<<'\n';
ans=max(ans,dp[i][j]);
}
}
}
cout<<ans*ans<<'\n';
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(j>1&&a[i][j-1]==a[i][j]) l[i][j]=l[i][j-1];
}
}
for(int i=1;i<=n;i++){
for(int j=m;j;j--){
if(j<m&&a[i][j+1]==a[i][j]) r[i][j]=r[i][j+1];
}
}
ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(i>1&&a[i][j]==a[i-1][j]){
l[i][j]=max(l[i][j],l[i-1][j]);
r[i][j]=min(r[i-1][j],r[i][j]);
h[i][j]=h[i-1][j]+1;
}
ans=max(ans,(r[i][j]-l[i][j]+1)*h[i][j]);
}
}
cout<<ans<<'\n';
return 0;
}
QOJ8933
fi,j表示i个事件,剩j个1分,最多0分的数量
此时2分数量=si-j
简单转移
QOJ9312
期望DP

QOJ8528
环上的线相交相当于区间相交
数据随机
答案不会太大(<900)
gi,j表示i,j最大匹配
满足单调性
fi,j表示满足gi,k=j的最小的k
转移考虑i是否匹配
若匹配,那么更新就是从 ri 继承过来加上 gi,ri 的答案
否则就是从 i + 1 继承
计数
GYM105336
容易发现如果一个 ai 和 bj 匹配了,那么 ai 后的元素与 bj 前的元素匹配对答案就不会产生改变了
考虑 答案 k 被确定时,方案可以简单算出
令 fi,j 表示前 i 个 a 匹配了 j 个 b 的方案数
每次枚举选不选即可转移
不难发现对于一个权值为 w 的方案,恰好在 k = 1~w 都被计算了一次
直接对所有 k 的答案求和即可得到所有匹配的权值和。
P2592
转化成网格计数
要求y-x极差<=k

(对称计算答案就是用类似卡特兰数的方法
卡特兰数公式:C(2n,n)-C(2n,n-2)
这个公式就是通过对称得来的)
复杂度O(n+m+k)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号