pyyzDay2
莫妮赛(远大于Day1)
T1 数字(number)
P11201 [JOIG 2024] たくさんの数字 / Many Digits
原题
考虑加法进位
总位数不会超过 10 位
考虑每个a[i]+b[j]的位数
若其位数为k+1
当且仅当10k≤a[i]+b[j]<10(k+1)
二分查找即可
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int a[200005],b[200005],tenth[11];
signed main()
{
//freopen("filename.in", "r", stdin);
//freopen("filename.out", "w", stdout);
int n=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<=n;i++) b[i]=read();
int go=1;
tenth[0]=1;
for(int i=1;i<=10;i++){
go*=10;
tenth[i]=go;
}
int ans=0;
sort(b+1,b+n+1);
for(int i=1;i<=n;i++){
for(int j=0;j<=10;j++){
int l=1,r=n;
int an=-1;
while(l<=r){
int mid=(l+r)>>1;
if(b[mid]+a[i]>=tenth[j]){
an=mid;
r=mid-1;
}
else l=mid+1;
}
l=1,r=n;
int an2=n+1;
while(l<=r){
int mid=(l+r)>>1;
if(b[mid]+a[i]<tenth[j+1]){
an2=mid;
l=mid+1;
}
else r=mid-1;
}
if(an2==n+1||an==-1) continue;
ans+=(j+1)*(an2-an+1);
}
}
cout<<ans<<'\n';
return 0;
}
T2 卡片(card)
原题
考虑图论建图
每张卡片的正反两个数字进行连边
因为是排列,所以一定有环
对环的大小进行计算答案
发现环的大小与答案有如下关系:
f1=1,f2=3,f3=4,f4=7,f5=11……
于是推断fi=fi-1+fi-2
why?
考虑一个点的覆盖情况。
对于某个点i,有选与不选两种情况:
1.选i,那么左右两相邻可选可不选,只选一个和俩都选时如果用fn−1则少算了俩都不选的情况,先记着。
2.不选i,那么左右两相邻必须都选,三变一但是带着必须选的buff,如果用fn−2则多算了两相邻都不选的情况。
但是我们先记着了,一多一少正好抵消。
不过OI不需要证明!!
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MOD=998244353;
int p[200005],q[200005];
vector<int> tu[200005];
int st[200005],top;
int len[200005],cnt;
int vis[200005];
int ann;
int f[200005],n;
void dfs(int x){
if(vis[x]){
len[++cnt]=top;
top=0;
return ;
}
vis[x]=1;
st[++top]=x;
for(auto ed:tu[x]){
dfs(ed);
}
}
signed main(){
// freopen("card.in","r",stdin);
// freopen("card.out","w",stdout);
cin>>n;
for(int i=1;i<=n;i++) cin>>p[i];
for(int i=1;i<=n;i++) cin>>q[i];
for(int i=1;i<=n;i++){
tu[p[i]].push_back(q[i]);
}
for(int i=1;i<=n;i++){
if(!vis[i]){
dfs(i);
}
}
f[1]=1;
f[2]=3;
for(int i=3;i<=200000;i++) f[i]=(f[i-1]+f[i-2])%MOD;
int ans=1;
for(int i=1;i<=cnt;i++){
ans=ans*f[len[i]]%MOD;
ans%=MOD;
}
cout<<ans<<'\n';
return 0;
}
T3 躲避滚石(rock)

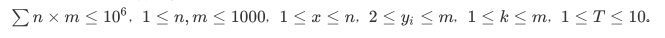
一个经典操作
考虑人动石头不动
设dp[i][j]表示能否到达i,j这个点
若x,y可达,则:
1.移动到(x,y+k),前提是(x,y)~(x,y+k)之间没有滚石。
2.移动到(x+1,y+k),前提是(x+1,y)~(x+1,y+k)之间没有滚石。
3.移动到(x−1,y+k),前提是(x−1,y)~(x−1,y+k)之间没有滚石。
可以前缀和预处理滚石个数方便区间查询
时间复杂度O(nm)
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int x[1000005],y[1000005],dp[5005][5005],sum[5005][5005];//sum,dp数组开大些,放溢出(可以不用long long)
void solve(){
int n=read(),m=read(),k=read(),p=read();
memset(dp,0,sizeof(dp));
memset(sum,0,sizeof(sum));
for(int i=1;i<=p;i++){
x[i]=read(),y[i]=read();
sum[x[i]][y[i]]++;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m+k;j++){//注意防止溢出需要更新到m+k
sum[i][j]+=sum[i][j-1];
}
if(!sum[i][1]) dp[i][1]=1;
}
for(int j=1;j<=m;j++){
for(int i=1;i<=n;i++){//注意枚举顺序防止覆盖
if(dp[i][j]){
if(sum[i][j+k]==sum[i][j-1]){
dp[i][j+k]=1;
if(j+k>=m){
cout<<"Yes"<<'\n';
return ;
}
}
if(i<n&&sum[i+1][j+k]==sum[i+1][j-1]){
dp[i+1][j+k]=1;
if(j+k>=m){
cout<<"Yes"<<'\n';
return ;
}
}
if(i>1&&sum[i-1][j+k]==sum[i-1][j-1]){
dp[i-1][j+k]=1;
if(j+k>=m){
cout<<"Yes"<<'\n';
return ;
}
}
}
}
}
cout<<"No"<<'\n';
}
signed main()
{
//freopen("filename.in", "r", stdin);
//freopen("filename.out", "w", stdout);
int T=read();
while(T--){
solve();
}
return 0;
}
T4 连通块(block)

n,m<=2e5
发现操作2其实是树的直径
考虑一种策略:正难则反
于是把删边变成加边
用并查集维护连通块
同时记录树的直径的长度以及两个端点
在维护连通块时,同样可以维护直径
新的直径两个端点一定在原先的两个联通块的直径端点的4个端点之中
新的直径可能是原先的两个联通块之一的直径,也可能经过新加的边
求LCA即可快速求出直径长度
(并非本人代码)
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define endl putchar('\n')
const int N=500005;
using namespace std;
int n,m,fa[N],a[N],b[N],f[N][20],cut[N],dep[N],ans[N];
int find(int x) { return x==fa[x]?x:fa[x]=find(fa[x]); }
vector<int> e[N];
struct dia { int a,b,dis; } d[N];
struct ques { int op,x; } q[N];
void dfs(int x,int fa) {
dep[x]=dep[fa]+1,f[x][0]=fa;
rep(i,1,19) f[x][i]=f[f[x][i-1]][i-1];
for(int to : e[x]) {
if(to!=fa) {
dfs(to,x);
}
}
}
int ask(int x,int y) {
if(dep[x]<dep[y]) swap(x,y);
for(int i=19;i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
if(x==y) return x;
for(int i=19;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
int get(int x,int y) { return dep[x]+dep[y]-2*dep[ask(x,y)]; }
dia mrg(dia x,dia y) {
dia t=x.dis>y.dis?x:y;
int res=get(x.a,y.a); t=t.dis>res?t:(dia){x.a,y.a,res};
res=get(x.a,y.b); t=t.dis>res?t:(dia){x.a,y.b,res};
res=get(x.b,y.a); t=t.dis>res?t:(dia){x.b,y.a,res};
res=get(x.b,y.b); t=t.dis>res?t:(dia){x.b,y.b,res};
return t;
}
void merge(int x,int y) {
int fx=find(x),fy=find(y);
fa[fx]=fy;
d[fy]=mrg(d[fx],d[fy]);
}
void init() {
dfs(1,0);
rep(i,1,n) {
fa[i]=i;
d[i]={i,i,0};
}
rep(i,1,n-1) {
if(!cut[i]) {
merge(a[i],b[i]);
}
}
}
void solve() {
for(int i=m;i>=1;i--) {
if(q[i].op==1) {
merge(a[q[i].x],b[q[i].x]);
} else {
int res=0,fx=find(q[i].x);
res=max(get(q[i].x,d[fx].a),get(q[i].x,d[fx].b));
ans[i]=res;
}
}
}
void file() {
freopen("block.in","r",stdin);
freopen("block.out","w",stdout);
}
int main() {
file();
scanf("%d%d",&n,&m);
rep(i,1,n-1) {
scanf("%d%d",&a[i],&b[i]);
e[a[i]].push_back(b[i]);
e[b[i]].push_back(a[i]);
}
rep(i,1,m) {
scanf("%d%d",&q[i].op,&q[i].x);
if(q[i].op==1) cut[q[i].x]=1;
}
init(),solve();
rep(i,1,m) {
if(q[i].op==2) printf("%d\n",ans[i]);
}
return 0;
}
T5 教室分组(group)

n<=1e6
人类智慧题
先将序列a排序,假设我们先固定一共分了多少组。
我们把一组划分成三部分,设这组作为中位数的位置称为B,那么把小于 a_B 的位置称为 A ,大于 a_B 的位置成为 C。
通过简单的观察可以发现,最优方案中最小的 B一定大于最大的 A,否则一定可以通过交换两者使答案不劣。
又因为 B 整体上越在数组后部答案越大,所以我们希望最小的 B 尽可能大,所以我们枚举最小 B 的位置,然后可以 0(1)来 check 是否存在一种方案满足枚举的位置,随后问题就变成了一个子问题,可以继续贪心解决。
这样如果固定了分多少组,那么可以 0(n)求最大值,总时间复杂度 O(n^2)。
考虑上述贪心选择的中位数的位置是分成两段的,前面一段和后面一段的下标都是一个等差数列。
前缀和维护累加答案即可
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int a[1000005],sum[100005],pre[1000005];
signed main()
{
//freopen("filename.in", "r", stdin);
//freopen("filename.out", "w", stdout);
int n=read(),l=read(),r=read();
for(int i=1;i<=n;i++){
a[i]=read();
}
sort(a+1,a+n+1);
l/=2;
r/=2;
for(int i=1;i<=n;i++){
if(i-r-1) sum[i]=sum[i-r-1]+a[i];
else sum[i]=a[i];
}
for(int i=n;i;i--){
if(i+l+1<=n) pre[i]=pre[i+l+1]+a[i];
else pre[i]=a[i];
}
int ans=0;
for(int i=1;i<=(n+1)/2;i++){
int A=i-1;
int B=n-2*(i-1);
int C=B*l;
if(C>A) continue;
A-=C;
int cnt=A/(r-l);
int su=0;
su+=sum[i+cnt*(r+1)];
if(i-r-1) su-=sum[i-r-1];
// if(B-cnt-1) su+=pre[n-(l+1)*(B-cnt-1)+1];
ans=max(ans,su/B);
}
cout<<ans<<'\n';
return 0;
}
拓展
我会树剖线段树!
注意边化点。
但是发现是区间推平,所以考虑有没有更优的解法。
区间推平最显著的性质就是取决于查询之前最后一次涉及到自己的操作。
所以我们可以直接跳过已经操作过的边。
如何跳?
并查集维护直接跳到根。
CF609D Gadgets for dollars and pounds
显然答案满足单调性。
考虑如何check。
直接按题意贪心模拟即可,排序找前k大的花费总合。
复杂度 nlog^2n。
怎么做到单 log ?
找最便宜的一天可以预处理前缀最小值。
将排序放在外面,两个有序数组直接按照归并排序的形式合并,无需再排,check的复杂度就是 O(n)的
[USACO24OPEN] Smaller Averages G
考虑dp,状态设计很清晰:设 f x,y 表示第一个数组划分到 x,第二个数组划分到 y 的方案数。
n4的暴力很好写,用前缀和维护,然后求一下平均值即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号