pyyzDay1
摸底考试(难于上青天)
T1 灭蚊(kill)

N<=1e5,ai<=1e9
题目简略就是:给定由 n 个非负整数组成的数列,每次可以删除一个数,求每次删除操作后的最大连续子序列
注意非负性质很重要
trick:正难则反
因为不强制在线,考虑倒着做
每插入一个数,拿并查集维护一下,记录答案,顺便取max
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int a[100005],sum[100005],fa[100005],ans[100005],b[100005];
int find(int x){
if(x==fa[x]) return x;
return fa[x]=find(fa[x]);
}
void merge(int x,int y){
int fx=find(x),fy=find(y);
if(fx==fy) return;
fa[fx]=fy;
sum[fy]+=sum[fx];
}
signed main()
{
//freopen("filename.in", "r", stdin);
//freopen("filename.out", "w", stdout);
int n=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<=n;i++) b[i]=read();
int an=0;
for(int i=n;i>=1;i--){
fa[b[i]]=b[i];
sum[b[i]]=a[b[i]];
if(fa[b[i]-1]) merge(b[i]-1,b[i]);
if(fa[b[i]+1]) merge(b[i]+1,b[i]);
an=max(an,sum[find(b[i])]);
ans[i]=an;
}
for(int i=2;i<=n;i++) cout<<ans[i]<<'\n';
cout<<0<<'\n';
return 0;
}
T2 区间逆序对(interval)
~~唯一一道原创~~
有一个长度为n的序列a,进行m次询问,每组询问中给定区间l,r,求区间逆序对个数
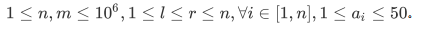
注意值域很小
区间逆序对容易想到前缀减前缀
然后再减去1-(l-1)对l-r的贡献
考虑贡献怎么做
预处理二维前缀和
sum[i][j]表示前i个数j出现的次数
查询时直接维护贡献
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int a[1000005],an[1000005],sum[1000005][55];
signed main()
{
//freopen("filename.in", "r", stdin);
//freopen("filename.out", "w", stdout);
int n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<=n;i++){
for(int j=1;j<=50;j++){
sum[i][j]=sum[i-1][j];
}
sum[i][a[i]]++;
an[i]=an[i-1];
for(int j=a[i]+1;j<=50;j++){
an[i]+=sum[i][j];
}
}
while(m--){
int u=read(),v=read();
int ans=an[v]-an[u-1];
int su=0;
for(int i=1;i<=50;i++){
ans-=su*sum[u-1][i];//减去1~r的贡献
su+=sum[v][i]-sum[u-1][i];
}
cout<<ans<<'\n';
}
return 0;
}
T3 01串(string)

贪心考虑几种情况
1.形如 01010,发现如果将中间的 0 填充,有 3 个贡献。这也是最大贡献
2.形如 10 或 01,发现将的 0 填充,有 2 个贡献。
3.形如 0,将其填充获得 1 个贡献。
注意不要重复,打个标记即可。
需要特判全0的情况
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){
if(b==0) return 1;
if(b==1) return a%p;
int c=ksm(a,b/2,p);
c=c*c%p;
if(b%2==1) c=c*a%p;
return c%p;
}
int n,q;
string s;
int vis[100005];
signed main()
{
//freopen("filename.in", "r", stdin);
//freopen("filename.out", "w", stdout);
cin>>n>>q;
cin>>s;
int fl=0;
for(int i=0;i<n;i++){
if(s[i]=='1'){
fl=1;
break;
}
}
if(!fl){
while(q--){
int k;
cin>>k;
if(k<2) cout<<0<<'\n';
else cout<<k<<'\n';
}
return 0;
}
int ans=0;
for(int i=1;i<n;i++){
if(s[i]=='1'&&s[i-1]=='1'){
ans++;
vis[i]=1;
if(!vis[i-1]){
ans++;
vis[i-1]=1;
}
}
}
int an3=0,an2=0;
for(int i=1;i<n;i++){
if(!vis[i]&&s[i]=='0'&&!vis[i-1]&&s[i-1]=='1'&&!vis[i+1]&&s[i+1]=='1'){
an3++;
vis[i]=vis[i-1]=vis[i+1]=1;
}
}
for(int i=1;i<n;i++){
if(!vis[i]&&s[i]=='0'&&!vis[i-1]&&s[i-1]=='1'){
an2++;
vis[i]=vis[i-1]=1;
}
else if(!vis[i]&&s[i]=='0'&&!vis[i+1]&&s[i+1]=='1'){
an2++;
vis[i]=vis[i+1]=1;
}
}
while(q--){
int k;
cin>>k;
if(k<=an3) cout<<ans+3*k<<'\n';
else if(k<=an3+an2) cout<<ans+3*an3+2*(k-an3)<<'\n';
else cout<<ans+3*an3+2*an2+k-an2-an3<<'\n';
}
return 0;
}
T4 运输(transport)

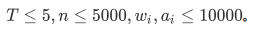
因为需要尽可能平均松果数量
直觉就是将松果多的减少,少的增多
易证,平均松果后任意两点间松果个数之差<=1
故设s=松果个数之和
则有s%n个点最终松果个数[s/n](下取整)+1
其余点为[s/n](下取整)
我们对于每条边分别计算
若一条边某一侧的子树中原来的权值之和与新的权值之和的差为d,则这条边至少会带来 dw 的贡献。
所以我们希望最小化dw之和。
考虑树形DP
设dp[u][k]表示以u为根的子树中有 k 个点的权值为 v+1 时子树内的最小代价
答案即为dp[1][s%n]
考虑转移
经典书上背包
复杂度O(n^2)
(复杂度证明考虑小子树向大子树合并)
std~
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5005;
const ll INF=1e18;
int t,n,a[N],s,h[N],tot,u,v,w,siz[N],c[N];
ll f[N][N];
struct edge
{
int to,val,nxt;
}e[N<<1];
void add(int u,int v,int w)
{
e[++tot]={v,w,h[u]};
h[u]=tot;
}
void dfs(int u,int fa)
{
siz[u]=1;f[u][0]=f[u][1]=0;
for(int i=h[u];i;i=e[i].nxt)
{
int v=e[i].to,w=e[i].val;
if(v==fa) continue;
c[v]=w;dfs(v,u);
for(int j=siz[u];j>=0;j--)
{
ll val=f[u][j];f[u][j]=INF;
for(int k=0;k<=siz[v];k++)
f[u][j+k]=min(f[u][j+k],val+f[v][k]);
}
siz[u]+=siz[v];a[u]+=a[v];
}
for(int i=0;i<=siz[u];i++) f[u][i]+=(ll)c[u]*abs(a[u]-i);
}
void solve()
{
memset(f,0x3f,sizeof(f));
scanf("%d",&n);s=0;tot=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
s+=a[i];h[i]=0;
}
for(int i=1;i<n;i++)
{
scanf("%d%d%d",&u,&v,&w);
add(u,v,w),add(v,u,w);
}
for(int i=1;i<=n;i++) a[i]-=(s/n);
dfs(1,0);s%=n;
printf("%lld\n",f[1][s]);
}
int main()
{
freopen("transport.in","r",stdin);
freopen("transport.out","w",stdout);
scanf("%d",&t);
while(t--) solve();
return 0;
}
T5 穿孔卡片(card)
P11088 [ROI 2021] 穿孔卡片 (Day 1)

N,M<=1e5
对目标字符串的每个位置进行分析
发现若不匹配,就一定要有卡片在它上面覆盖
当某张卡片成功匹配某点,剩下的所有卡片这个点都可匹配
这种限制发现很像拓扑排序
对于第i张卡片
所有不匹配的点向它连边
再向所有匹配的点连边
拓扑排序即可求出答案
别忘了环无解
std~
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+15;
int n,m,hd=1,tl,q[N],vist[N],visp[N],f[N];//vist[i]:卡片i是否被使用 visp[i]:位置i是否被覆盖
vector<int>ans,p[N],g[N];//p[i]:卡片i覆盖的位置 g[i]:所有不匹配的点
char c,s[N];
int main(){
freopen("card.in","r",stdin);
freopen("card.out","w",stdout);
scanf("%d%d",&n,&m);
scanf("%s",s+1);
for(int k,j,i=1;i<=n;++i){
scanf("%d",&k);
while(k--){
scanf("%d %c",&j,&c);
p[i].push_back(j);
if(s[j]!=c)++f[i],g[j].push_back(i);//模拟
}
if(!f[i])q[++tl]=i;//模拟
}
int cnt=m;
for(int w;hd<=tl;){
ans.push_back(w=q[hd++]),vist[w]=true;//取出一个f值为0的卡片w
for(int i:p[w]){
if(visp[i]==true)continue;
--cnt,visp[i]=true;//遍历w覆盖的所有位置
for(int j:g[i]){
if(!--f[j])q[++tl]=j;//更新
}
}
if(!cnt){
for(int i=1;i<=n;++i){if(!vist[i])ans.push_back(i);}
for(int i:ans)printf("%d ",i);
return 0;
}
}
printf("-1");//(cnt!=0 && q.empty()==true)
return 0;
}
课后拓展题
CF915F Imbalance Value of a Tree
并查集模板题。
考虑如果是边权怎么做。
考虑从小到大加入每一条边(x,y,w),并计算贡献 ans+=w×S_x×S_y,其中 S_i表示 i 所在的连通块大小。
点权怎么办?
小tips:化点为边,边 (x,y) 的权值 =max(w_x ,w_y ) , 其中 w_i 表示 i 的点权。
显然 min 一样。
(化边为点:每个点表示该点向父亲的边权)
CF148E Porcelain
因为每一次都只能去边上的,所以取完后还是一个区间,考虑前缀和。
预处理出每一层取若干个的最大价值。
每一层显然只会转移一个状态。
分组背包。
CF2113F Two Arrays
考虑答令 cnt_i 表示 i 的出现总次数,显然有答案上界 ∑min( cnt_i ,2)
两个数组,显然每一位上只有交换与不交换两种可能。我们希望每个出现次数大于2的数字在 a 中和在 b 中至少都出现过一次。
考虑建无向图,定向。
问题转换为使得所有度数大于等于 2 的点至少一条出边和一条入边。
对于每个联通块,考虑从度数为1的点开始搜,将返祖边指回来即可,构建环。
没有一度数点呢?随便找一个环上的点当起点。
于是想到欧拉路径,题意进一步转化:尽量让出度和入度相同(差不超过1)。
显然可以跑欧拉回路构造答案。
但是可能有奇度数点。。
连起来!
奇度点任意两两配对连边,因为奇度数点必定有偶数个,求欧拉回路即可,按欧拉回路定向,再删掉添加的边即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号