POJ 3253 Fence Repair （优先队列）

d题目链接： POJ  3253

Describe:

Farmer John wants to repair a small length of the fence around the pasture. He measures the fence and finds that he needs N (1 ≤ N ≤ 20,000) planks of wood, each having some integer length L_i (1 ≤ L_i ≤ 50,000) units. He then purchases a single long board just long enough to saw into the N planks (i.e., whose length is the sum of the lengths L_i). FJ is ignoring the "kerf", the extra length lost to sawdust when a sawcut is made; you should ignore it, too.

FJ sadly realizes that he doesn't own a saw with which to cut the wood, so he mosies over to Farmer Don's Farm with this long board and politely asks if he may borrow a saw.

Farmer Don, a closet capitalist, doesn't lend FJ a saw but instead offers to charge Farmer John for each of the N-1 cuts in the plank. The charge to cut a piece of wood is exactly equal to its length. Cutting a plank of length 21 costs 21 cents.

Farmer Don then lets Farmer John decide the order and locations to cut the plank. Help Farmer John determine the minimum amount of money he can spend to create the N planks. FJ knows that he can cut the board in various different orders which will result in different charges since the resulting intermediate planks are of different lengths.

Input:

Line 1: One integer N, the number of planks
Lines 2..N+1: Each line contains a single integer describing the length of a needed plank

Output:

Line 1: One integer N, the number of planks
Lines 2..N+1: Each line contains a single integer describing the length of a needed plank

Sample Input:

3
8
5
8

Sample Output:

34

 题目大意：

有根木棍，要用这根木棍得到N条长度不一定相同的小木棍，每锯一次，所花费的钱为当前木棍长度，问要得到所需的木棍，所花费最少钱是多少。

解题思路：

每次锯的花费时当前木棍长度，其实就是锯完以后得到的两根木棍长度之和，我们可以用一棵二叉树来描述一下，如图

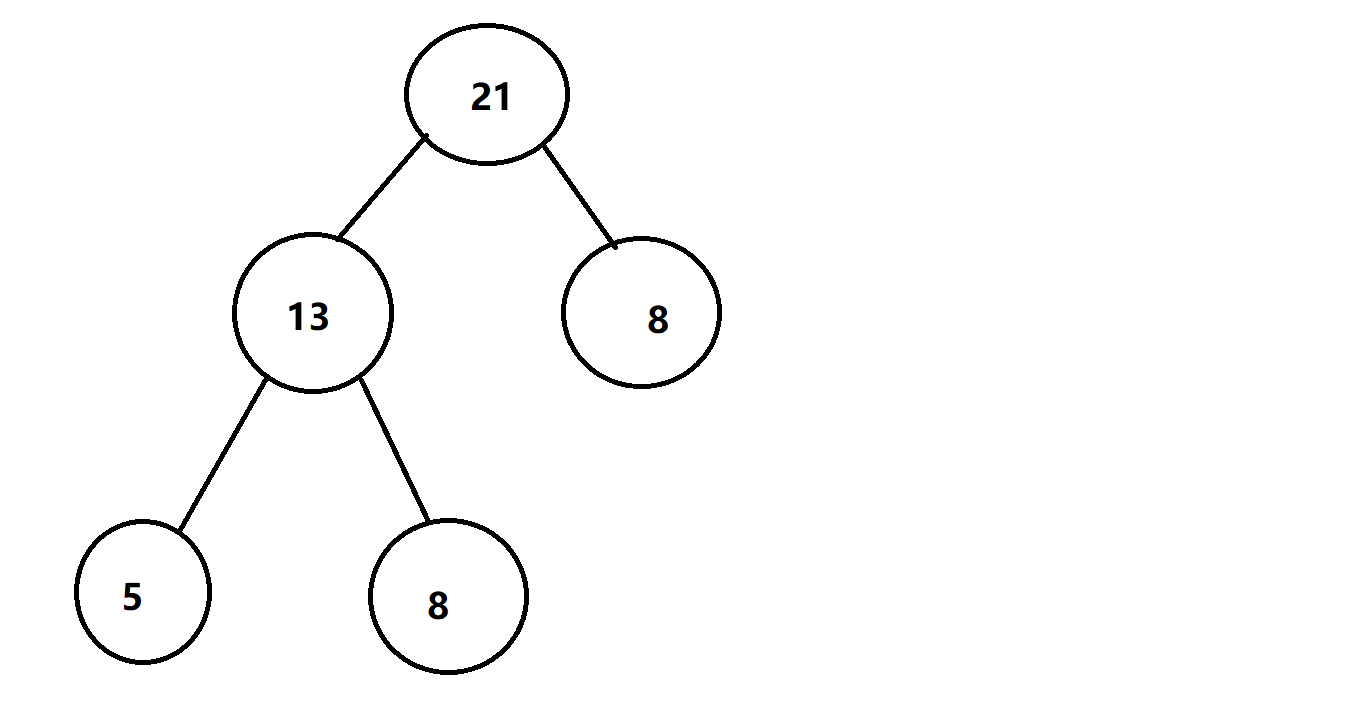
假设有一根长度21的棍子，要得到5 8 8长度的棍子，首先锯第一次花费21，锯第二次花费13，即这棵树的带权路径长度，想到哈夫曼树。用小顶堆来实现，每次取堆中最小的两个元素相加，再将和加入堆中，最终堆中的元素即为答案。（树的带权路径长度的求法）

AC代码：

#include <iostream>
#include <queue>
#include <cstdio>
#define ll long long // 注意数据范围，int有可能溢出
using namespace std;
int main()
{
    ll n,x,s,c,a,b;
    c = 0;
    scanf("%lld",&n);
    priority_queue <ll, vector<ll>, greater<ll> > q;
    for(ll i = 0; i < n; i++)
    {
        scanf("%lld",&x);
        q.push(x);
    }
    while(q.size() != 1)
    {
        a = q.top();
        q.pop();
        b = q.top();
        q.pop();
        c += a+b;
        q.push(a+b);
    }
    cout << c;
    return 0;
}