二分搜索树
二分搜索树
树 结构是一种天然的组织结构
二分搜索树（Binary Search Tree）
平衡二叉树：AVL、红黑树
堆；并查集
线段树；Trie（字典树，前缀树）
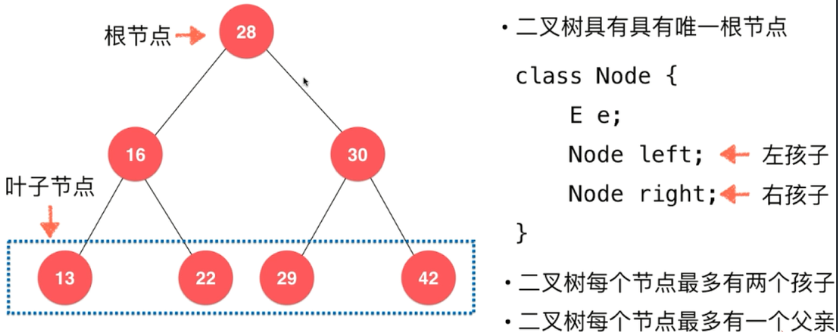
二叉树
class Node {
E e;
Node left;
Node right;
}
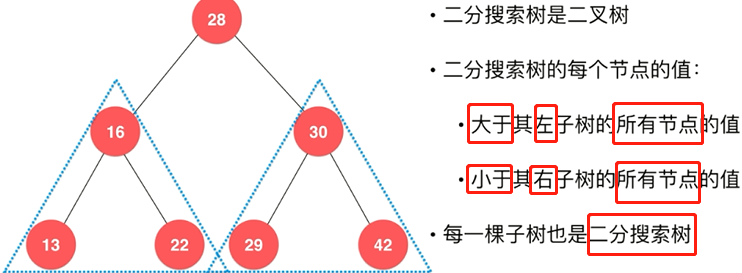
二分搜索树
Binary Search Tree
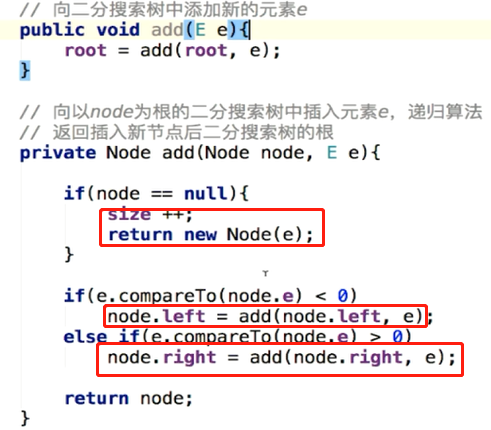
以下均为递归实现：
插入元素
查询是否含有元素
遍历
-
深度优先遍历
- 前序遍历
- 后序遍历
- 中序遍历
-
广度优先遍历 更快地找到要查询的元素，主要用于搜索。常用于算法设计--最短路径
- 层序遍历
前序遍历
先访问节点，再访问左 右子树。
对于下面这样的二叉树，前序遍历的输出 为 5 3 2 4 6 8
递归写法：
非递归写法：借助 栈 来完成遍历，先入栈 右孩子，后入栈左孩子，因为栈先进后出
中序遍历：
先访问节点的左子树，再 根点 ，再右子树
2 3 4 5 6 8
中序遍历的结果就是二分搜索树顺序排序后的结果。
非递归写法：
看那一下非递归写法
网上搜
后序遍历
先访问节点左子树，右子树，再访问节点
输出 2 4 3 8 6 5
后序遍历的应用：内存释放
非递归写法：
看那一下非递归写法
网上搜
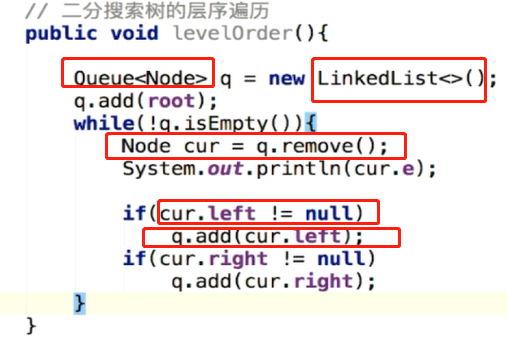
层序遍历
是广度优先遍历。
一层一层遍历， 左右 孩子。
借助队列queue 完成遍历 ，先进先出。
思路：
先 将根节点放入队列中，然后开始循环判断
如果队列q不为空，出队队首 节点
判断队首节点是否有左右子树，并入队 左子树，右子树
再循环 判断 q是否为空，出队
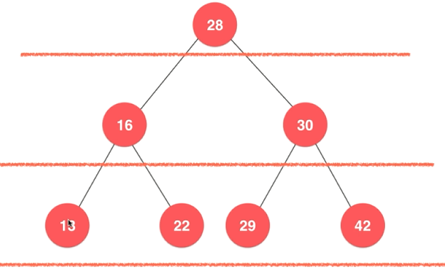
查询最大/小元素
二分搜索树的最大元素是 最右的一个节点
最小元素是最左的一个节点
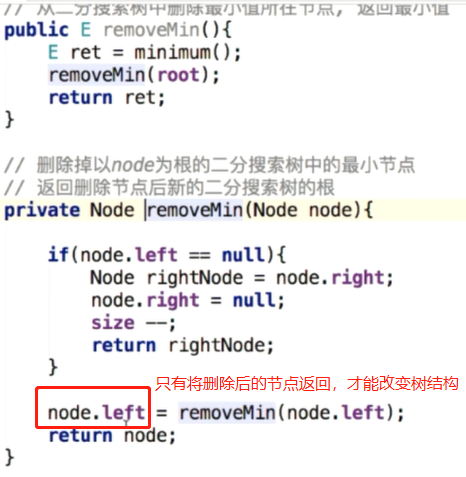
删除最小/大值
有可能是叶子节点；也可能不是叶子节点
删除任意元素
-
删除只有左孩子的节点： 将左孩子节点存在另一个变量，再置null原节点，再将节点的左子树返回；
-
删除只有右孩子的节点： 将右孩子节点存在另一个变量，再置null原节点，再将节点的右子树返回，即
if(node.left == null){ Node rightNode = node.right; node = null; size --; return rightNode; } -
删除左右都有孩子的节点：
方法： 用左子树的最大节点 或者 右子树 的最小节点 替代 原节点
predecessor：前驱：左子树中最大的，
successor ：后继：右子树中最小的
// 从二分搜索树中删除元素为e的节点
public void remove(E e){
root = remove(root, e);
}
// 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
private Node remove(Node node, E e){
if( node == null )
return null;
if( e.compareTo(node.e) < 0 ){
node.left = remove(node.left , e);
return node;
}
else if(e.compareTo(node.e) > 0 ){
node.right = remove(node.right, e);
return node;
}
else{ // e.compareTo(node.e) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// 待删除节点右子树为空的情况
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
更多二分搜索树相关知识点：
floor
ceil
rank
select
size：有几个节点
depth
重复元素：每个node 加 count 属性
