谈对牛顿法的理解
牛顿法
牛顿啊和拟牛顿法都是求解无约束最优化问题得常用方法,有收敛速度快的特点。这是因为有些时候我们需要求解最优化的函数过于复杂直接对其求导很也不能计算出极值。便可以采用一些极值收敛算法,除了牛顿法和拟牛顿法之外,比如还有梯度上升和梯度下降的收敛算法。
- 牛顿法
考虑无约束优化问题
![在这里插入图片描述]()
这里x就是函数f(x)的变量,我们需要做的就是,找出一个x使得f(x)最小,同时x 是一个n维的变量。
牛顿法的基本思想就是:在现有极小点估计点的附近对f(x)进行二阶泰勒展开,然后再次计算现在展开函数的极值,不断迭代直至收敛。
如下式,若n=1,拿单变量的情况举个例子
![在这里插入图片描述]()
此时若我们假设Xk为极小值点,现以f(x)关于Xk展开泰勒展开式,此时展开的函数则应该近似f(x),也就是上式应该近似f(x)此时我们再对上式求导,求极值,得到的就是上式的极值点,即下式
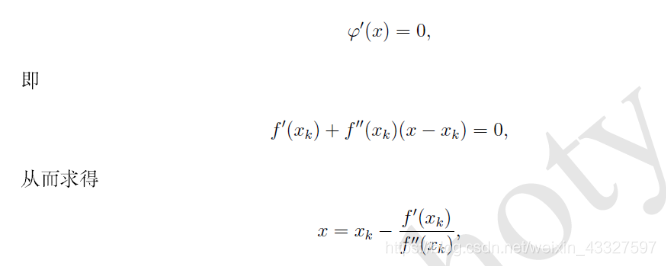
这里有些人可能有些疑问
1.Xk初始值可以随便取吗,如果可以为什么?
2.为什么能用展开后的函数求极值来收敛得到我们想要的结果?
3.为什么不断手迭代会收敛,难道不会不断偏离真实极值点吗?
Xk时初始值是可以随机取得,但不要太离谱,比如收敛点在0-100,你初始值取个上千万就太不靠谱了。展开后的泰勒函数本质上始是与原函数相似的,但因为只展开到二阶,所以也有一定偏差。同**时我们可以知道,对于低阶泰勒展开函数当与展开点越远时越偏离原函数,当与展开点越近时越接近原函数。**所以如果我们上述算法可以不断收敛以至于X(k+1)十分接近Xk时说明此时在Xk点处展开函数十分接近原函数,也就是在Xk处展开函数图像和原函数图像几乎一致,那么X(k+1)可以认为是原函数的极值点,因为它是展开函数的极值点,两个函数又很相似。
现在问题关键是为什么不断迭代X(k+1)会不断接近Xk?
这个问题我就不解释了,大家可以结合函数图像来思考这个问题,确实是可以收敛的。
牛顿法的问题,认真看我的这篇博客的话,如果用牛顿法求解最优解的时候,牛顿法可能会陷入局部最优解。因为收敛时f’(x)=0,一个函数可能不只一个极小值。



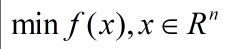
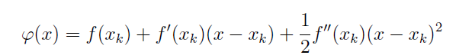

 浙公网安备 33010602011771号
浙公网安备 33010602011771号