BGD&SGD&&Mini-BGD
站在大佬肩膀上看世界的感觉可真是爽~
希望大佬勿拍砖~
各种梯度下降
从梯度下降讲起,至于为什么要学习梯度下降,你可以理解为:咱们人啊往往在做一件事的时候不会有一个完美的方法直接全部搞完,而是一步一步的去搞,积跬步至千里~
在应用机器学习算法时, 我们通常采用梯度下降法来对采用的算法进行训练。其实, 常用的梯度下 降法还具体包含有三种不同的形式, 它们也各自有着不同的优缺点。
下面我们以线性回归算法来对三种梯度下降法进行比较。
一般线性回归函数的假设函数为:
对应的损失函数为:
(这里的1/2是为了后面求导计算方便) 下图作为一个二维参数 \(\left(\theta_{0}, \theta_{1}\right)\) 组对应能量函数的可视化图

批量梯度下降法BGD(也是全量)
我们的目的是要误差函数尽可能的小,即求解weights使误差函数尽可能小。首先,我们随机初始化weigths,然后不断反复的更新weights使得误差函数减小,直到满足要求时停止。这里更新算法我们选择梯度下降算法,利用初始化的weights并且反复更新weights:
这里 \(\alpha\) 代表学习率,表示每次向着J最陡肖的方向迈步的大小。为了更新weights,我们需要求出 函数J的偏导数。首先当我们只有一个数据点(x,y)的时候,J的偏导数是:
\(\begin{aligned} \frac{\partial}{\partial \theta_{j}} J(\theta) &=\frac{\partial}{\partial \theta_{j}} \frac{1}{2}\left(h_{\theta}(x)-y\right)^{2} \\ &=2 \cdot \frac{1}{2}\left(h_{\theta}(x)-y\right) \cdot \frac{\partial}{\partial \theta_{j}}\left(h_{\theta}(x)-y\right) \\ &=\left(h_{\theta}(x)-y\right) \cdot \frac{\partial}{\partial \theta_{j}}\left(\sum_{i=0}^{n} \theta_{i} x_{i}-y\right) \\ &=\left(h_{\theta}(x)-y\right) x_{j} \end{aligned}\)
则对所有数据点,上述损失函数的偏导(累和)为:
再最小化损失函数的过程中,需要不断反复的更新weights使得误差函数减小,更新过程如下:
因此每次参数更新的伪代码
repeat
[
\begin{aligned}
\theta_{j}^{\prime} &=\theta_{j}+\frac{1}{m} \sum_{i=1}{m}\left(y-h_{\theta}\left(x^{i}\right)\right) x_{j}^{i} \
&(\text { for every } \mathrm{j}=0, \ldots, n)
\end{aligned}
]
由上图更新公式我们就可以看到,我们每一次的参数更新都用到了所有的训练数据(比如有m个,就用到了m个),如果训练数据非常多的话,是非常耗时的。
下面给出批梯度下降的收敛图:
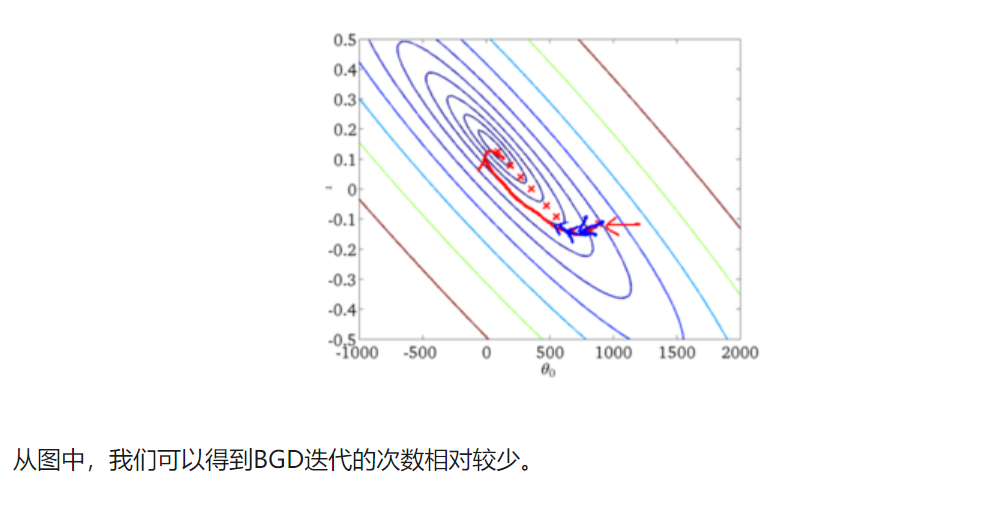
随机梯度下降法SGD(可以理解为一个一个的样本进心更新)
由于批梯度下降每跟新一个参数的时候,要用到所有的样本数,所以训练速度会随着样本数量的增加而变得非常缓慢。随机梯度下降正是为了解决这个办法而提出的。它是利用每个样本的损失函数对θ求偏导得到对应的梯度,来更新θ:
\(\theta_{j}=\theta_{j}+\left(y^{i}-h_{\theta}\left(x^{i}\right)\right) x_{j}^{i}\)


min-batch 小批量梯度下降法MBGD
我们从上面两种梯度下降法可以看出,其各自均有优缺点,那么能不能在两种方法的性能之间取得一个折衷呢?即,算法的训练过程比较快,而且也要保证最终参数训练的准确率,而这正是小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)的初衷。
我们假设每次更新参数的时候用到的样本数为10个(不同的任务完全不同,这里举一个例子而已)

#coding=utf-8
import numpy as np
import random
#下面实现的是批量梯度下降法
def batchGradientDescent(x, y, theta, alpha, m, maxIterations):
xTrains = x.transpose() #得到它的转置
for i in range(0, maxIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis - y
# print loss
gradient = np.dot(xTrains, loss) / m #对所有的样本进行求和,然后除以样本数
theta = theta - alpha * gradient
return theta
#下面实现的是随机梯度下降法
def StochasticGradientDescent(x, y, theta, alpha, m, maxIterations):
data = []
for i in range(10):
data.append(i)
xTrains = x.transpose() #变成3*10,没一列代表一个训练样本
# 这里随机挑选一个进行更新点进行即可(不用像上面一样全部考虑)
for i in range(0,maxIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis - y #注意这里有10个样本的,我下面随机抽取一个进行更新即可
index = random.sample(data,1) #任意选取一个样本点,得到它的下标,便于下面找到xTrains的对应列
index1 = index[0] #因为回来的时候是list,我要取出变成int,更好解释
gradient = loss[index1]*x[index1] #只取这一个点进行更新计算
theta = theta - alpha * gradient.T
return theta
def predict(x, theta):
m, n = np.shape(x)
xTest = np.ones((m, n+1)) #在这个例子中,是第三列放1
xTest[:, :-1] = x #前俩列与x相同
res = np.dot(xTest, theta) #预测这个结果
return res
trainData = np.array([[1.1,1.5,1],[1.3,1.9,1],[1.5,2.3,1],[1.7,2.7,1],[1.9,3.1,1],[2.1,3.5,1],[2.3,3.9,1],[2.5,4.3,1],[2.7,4.7,1],[2.9,5.1,1]])
trainLabel = np.array([2.5,3.2,3.9,4.6,5.3,6,6.7,7.4,8.1,8.8])
m, n = np.shape(trainData)
theta = np.ones(n)
alpha = 0.1
maxIteration = 5000
#下面返回的theta就是学到的theta
theta = batchGradientDescent(trainData, trainLabel, theta, alpha, m, maxIteration)
print "theta = ",theta
x = np.array([[3.1, 5.5], [3.3, 5.9], [3.5, 6.3], [3.7, 6.7], [3.9, 7.1]])
print predict(x, theta)
theta = StochasticGradientDescent(trainData, trainLabel, theta, alpha, m, maxIteration)
print "theta = ",theta
x = np.array([[3.1, 5.5], [3.3, 5.9], [3.5, 6.3], [3.7, 6.7], [3.9, 7.1]])
print predict(x, theta)
#yes,is the code
总结
三种梯度下降方法的总结
1.批梯度下降每次更新使用了所有的训练数据,最小化损失函数,如果只有一个极小值,那么批梯度下降是考虑了训练集所有数据,是朝着最小值迭代运动的,但是缺点是如果样本值很大的话,更新速度会很慢。
2.随机梯度下降在每次更新的时候,只考虑了一个样本点,这样会大大加快训练数据,也恰好是批梯度下降的缺点,但是有可能由于训练数据的噪声点较多,那么每一次利用噪声点进行更新的过程中,就不一定是朝着极小值方向更新,但是由于更新多轮,整体方向还是大致朝着极小值方向更新,又提高了速度。
3.小批量梯度下降法是为了解决批梯度下降法的训练速度慢,以及随机梯度下降法的准确性综合而来,但是这里注意,不同问题的batch是不一样的,听师兄跟我说,我们nlp的parser训练部分batch一般就设置为10000,那么为什么是10000呢,我觉得这就和每一个问题中神经网络需要设置多少层,没有一个人能够准确答出,只能通过实验结果来进行超参数的调整。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号