EOJ-3300 奇数统计(高维前缀和)
题目链接:
https://acm.ecnu.edu.cn/problem/3300/
题目大意:
给n个数,求在n个数中选两个数(可重复),使得这两个数的组合数是奇数,求总共有多少种取法。
解题思路:
组合数Cnm奇偶性判断:
n & m == m 成立则组合数为奇数
一开始没什么的思路,直接暴力超时,后来看到Lucas定理,发现上面那个式子的本质就是从这里推导出来的。
Lucas定理:

组合数判断奇数的话就是转化成上述定理中p = 2
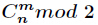

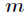
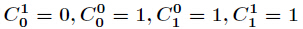

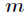
这样n&m = m的本质就是二进制中n对应的0得地方,m也对应为0。
然而,就是这个本质,就可以解这道题目
有位大佬一句话点醒了我,n&m = m说明m是n的子集。
对的,用二进制表示子集的时候,就是这样,m是n的子集,等价于n为0的位置m一定为0,n为1
的位置,m可以为1,可以为0。
然后对于每个n,求出它的子集的数目即可。
对于求子集,大佬教的方法是高维前缀和,代码很简单,就三行,和状态压缩DP一样。
1 for(int i = 0; i < m; i++) 2 { 3 for(int j = 0; j < (1<<m); j++) 4 { 5 if(j & (1<<i)) 6 sum[j] += sum[j ^ (1<<i)]; 7 } 8 }
举个例子,sum[0101] = sum[0101] + sum[0100] + sum[0001] + sum[0000]
sum[i]就表示i二进制的所有子集的权值之和
对于组合数n & m == m m是n的子集,
先统计每个数出现的次数,然后对于每个数,统计它的子集的个数即可,最后答案相加。
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn = 1e6 + 10; 4 typedef long long ll; 5 ll a[maxn], sum[maxn]; 6 int main() 7 { 8 int T, n, x; 9 cin >> T; 10 while(T--) 11 { 12 scanf("%d", &n); 13 memset(a, 0, sizeof(a)); 14 memset(sum, 0, sizeof(sum)); 15 for(int i = 0; i < n; i++) 16 { 17 scanf("%d", &a[i]); 18 sum[a[i]]++; 19 } 20 int m = 17; 21 for(int i = 0; i < m; i++) 22 { 23 for(int j = 0; j < (1<<m); j++) 24 { 25 if(j & (1<<i)) 26 sum[j] += sum[j ^ (1<<i)]; 27 } 28 } 29 ll ans = 0; 30 for(int i = 0; i < n; i++) 31 ans += sum[a[i]]; 32 cout<<ans<<endl; 33 } 34 return 0; 35 }
越努力,越幸运




 浙公网安备 33010602011771号
浙公网安备 33010602011771号