差分约束系统
1.差分约束系统
假设有这样一组不等式
X1-X2 <= 0
X1-X5 <= -1
X2-X5 <= 1
X3-X1 <= 5
X4-X1 <= 4
X4-X3 <= -1
X5-X3 <= -3
X5-X4 <= -3
每个不等式都是两个未知数的差小于等于某个常数(大于等于也行,因为左右*-1即可)。这样的不等式组称为差分约束系统
这个不等式组要么无解,要么无数组解,因为如果有一组解{X1, X2, ...Xn},那么每个数字加上常数k也满足不等式,因为两个数同时加上k,他们之间的差不变。
2.差分约束系统和最短路径
此处应有传送门:
*SPFA
(*表示重点)
差分约束系统的求解需要利用单源最短路径问题中的三角形不等式,即对于有向图(无向图)中的任何一条边<u, v>都有:
d[v] <= d[u] + Edge[u][v]
式中d[u]和d[v]表示从原点分别到顶点u,v的最短路径的长度,Edge[u][v]是边的权值。式子显然成立,可参考上述链接Bellman-Ford算法中的松弛过程讲解。
上面的不等式可以转化成d[v] - d[u] <= Edge[u][v]
3.有向图的构造
构造方法:
每个不等式中的未知数Xi对应图中的一个顶点Vi,把所有不等式Xi-Xj<=c转化成边<Vj. Vi>,权值为c
最后加入一个源点X0,由于三角不等式,索性把源点0到其他点的距离设置成0,以上述例子为例,就多出下面5条不等式
X1 - X0 <= 0
X2 - X0 <= 0
X3 - X0 <= 0
X4 - X0 <= 0
X5 - X0 <= 0
根据上述不等式,可以建出下图:

构件好图之后,以V0为源点,求单源最短路径,由于存在负权边,所以只能用Bellman-Ford求解,最终得到V0到个点的最短路径就是上述差分约束系统的一组解
如上图,{-5,-3,0,-1,4}就是一组解,如果把每个数字加上10也满足之前的不包括X0的不等式,但是这是无关紧要的,因为X0本来就是后来加上去的,满不满足X0有关的式子并不影响原来不等式组的解。
关于源点V0的取值,对于{-5,-3,0,-1,4}来说V0取的是0,因为本来就求源点到某点的最短路径长度,源点到自己本身的距离就是0。
4.差分约束系统无解的情况
如果建设的有向图中存在负权值回路(负环),那么就是无解。
X1 - X5 <= -5
X4 - X1 <= 3
X5 - X4 <= -1
上述三式相加得0 <= -3,无解
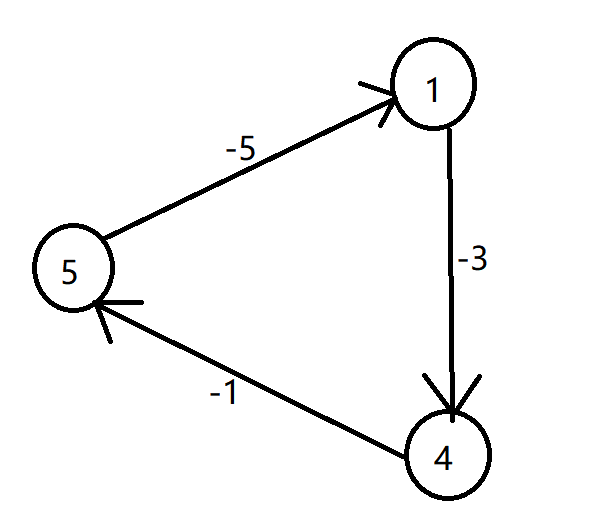
差分约束系统求最大值时,构造边按照:d[v] - d[u] <= Edge[u][v] (u->v连边),求解时按照最短路求解(也就是松弛的时候按照原来的方式进行松弛)
求最小值时,构造边按照:d[v] - d[u] >= Edge[u][v](u->v连边),求解时按照最长路进行求解(松弛的时候和原来相反)
权值为正的时候还可以用dijkstra


