P5323[BJOI2019]光线
//时隔一年,终于又写博客了!(大概是最后一篇博客了吧)之所以写这篇博客呢,是用来纪念我AC600祭(我肯定不会说我是闲得无聊来打发时间的),废话不多说,直接进入正题:
[BJOI2019]光线
题目描述
当一束光打到一层玻璃上时,有一定比例的光会穿过这层玻璃,一定比例的光会被反射回去,剩下的光被玻璃吸收。
设对于任意 \(x\),有 \(x \times a_i\%\) 单位的光会穿过它,有 \(x \times b_i\%\) 的会被反射回去。
现在 \(n\) 层玻璃叠在一起,有 \(1\) 单位的光打到第 \(1\) 层玻璃上,那么有多少单位的光能穿过所有 \(n\) 层玻璃呢?
输入格式
第一行一个正整数 \(n\),表示玻璃层数。
接下来 \(n\) 行,每行两个非负整数 \(a_i,b_i\),表示第 \(i\) 层玻璃的透光率和反射率。
输出格式
输出一行一个整数,表示穿透所有玻璃的光对 \(10^9 + 7\) 取模的结果。
可以证明,答案一定为有理数。设答案为 \(a/b\) ( \(a\) 和 \(b\) 是互质的正整数),你输出的答案为 \(x\),你需要保证 \(a\equiv bx \space (\text{mod }10^9 + 7)\)。
样例 #1
样例输入 #1
2
50 20
80 5
样例输出 #1
858585865
样例 #2
样例输入 #2
3
1 2
3 4
5 6
样例输出 #2
843334849
提示
样例1解释:
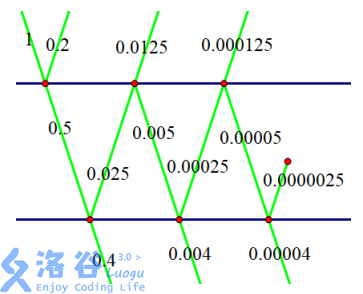
如图,光线从左上角打进来,有 \(0.5\) 单位的光穿过第 \(1\) 层玻璃,有 \(0.2\) 单位的光被反射回去。这 \(0.5\) 单位的光有 \(0.4\) 单位穿过第 \(2\) 层玻璃,有 \(0.025\) 单位的光被反射回去。这 \(0.025\) 单位的光有 \(0.0125\) 单位穿过第 \(1\) 层玻璃,有 \(0.005\) 单位的光被反射回去。这 \(0.005\) 单位的光有 \(0.004\) 单位穿过第 \(2\) 层玻璃……于是,穿过两层玻璃的光一共有\(0.40404... = 40/99\) 单位。在模 \(10^9+7\) 意义下等于 \(858585865\)
说实话,一读题第一反应竟是“bjoi就这?”但是,看完样例的分析我傻了,是我理解错题意了······赶紧从头又分析了一遍,感觉没问题了,便开始敲代码,结果敲了半个小时发现,好像还没有完全理解,再一次回头分析了一下样例(这提醒我们,一定要审好题,理解题意后在动手,要不然就会像我一样,浪费时间),发现第一面和最后一面的反射率是不一样的,我竟然还天真的认为反射率是一样的,不过透光率是一样的(经过计算可知),所以呢,这样就很容易了,只需要维护两个变量即可:
1、光从第 1 面玻璃射入时的透光率。
2、光从第 i 面玻璃射入时的反射率。
\(p_i=p_{i-1}a_i\sum_{k=0}^\infty(q_{i-1}b_i)^k\)
\(q_i=b_i+q_{i-1}a_i^2\sum_{k=0}^\infty(q_{i-1}b_i)^k\)
其中,还可以进一步优化:带有\(\sum_{k=0}^\infty a^k\)的形式,当\(|a|\)<1时,它等于\(\frac{1}{1-a}\)
所以:
\(P_i=\frac{P_{i-1}a_i}{1-Q_{i-1}b_i}\)
\(Q_i=b_i+\frac{Q_{i-1}a_i^2}{1-Q_{i-1}b_i}\)
可以先计算出\(\frac{1}{1-Q_{i-1}b_i}\)简化计算
最后,贴上代码:
#include<bits/stdc++.h>
#define N 1000010
#define int long long
#define INF 0x3f3f3f3f
const int Mod = 1e9 + 7;
const int Inv100 = 570000004;//(pow(100, Mod - 2));
#define ld long double
#define M 1010
#define R register int
using namespace std;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') f=-1;
ch=getchar();
}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+ch-'0';
ch=getchar();
}
return x*=f;
}
inline void write(int x){
if(x<0){
putchar('-');
x=-x;
}
if(x>9)
write(x/10);
putchar(x%10+'0');
}
int n;
int p, q;//p:前 i 面玻璃按顺序叠在一起后,光从第 1 面玻璃射入时的透光率。
//q:前 i 面玻璃按顺序叠在一起后,光从第 i 面玻璃射入时的反射率。
inline int Inv(int x){
int a = 1;
for (int i = Mod - 2; i; i >>= 1){
if(i&1) a = a * x % Mod;
x = x * x % Mod;
}
return a;
}
signed main(){
n = read();
p = 1, q = 0;
while(n--){
int a = read(), b = read();
a = a * Inv100 % Mod;
b = b * Inv100 % Mod;
int d = Inv(1 - q * b % Mod + Mod) % Mod;
q = (b + a * a % Mod * q % Mod * d) % Mod;
p = p * a % Mod * d % Mod;
}
write(p);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号