BUAA OO Unit3总结

BUAA OO Unit3 总结

1 架构设计

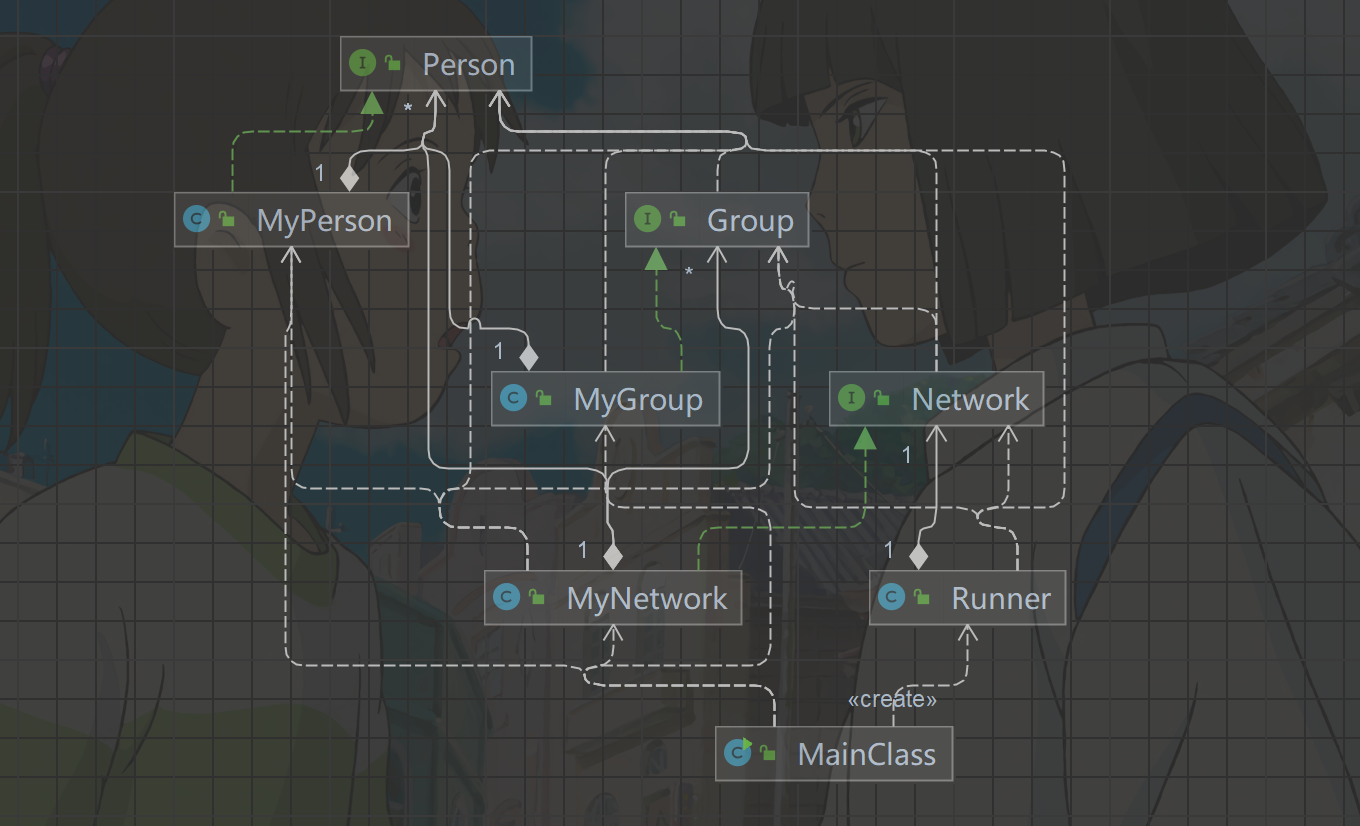
1.1 Homework9

第九次作业训练目标是实现简单社交关系的模拟和查询。本次作业我一共实现了MyPerson、MyGroup、MyNetwork以及六个异常类。

• MyPerson：
  • 每一个由MyPerson类实例化的对象都是一个人，可以抽象为一个结点，有自己的name、age和独一无二的id，acquaintance和value分别是有关系的人的集合以及对应的value的集合。
  • 每个MyPerson结点和acquaintance集合里面的结点之前都可以抽象为有一条边，对应的value值就是边的权重。
• MyGroup：
  • MyGroup相当于是一群人的集合，同时拥有自己的独一无二的id。
• MyNetwork：
  • MyNetwork中的people是所有人的集合，groups是所有MyGroup的集合。

具体关系如下：

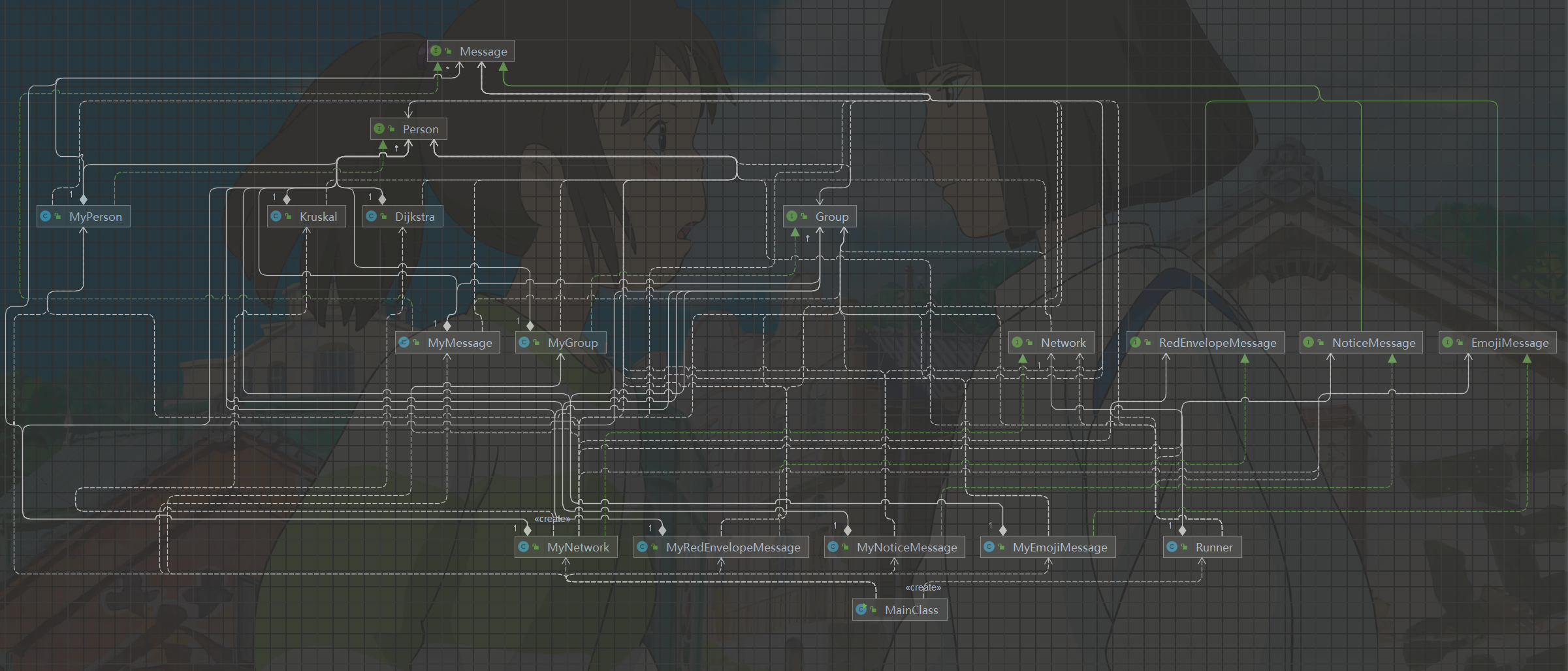
1.2 Homework10

和Homework9相比，本次作业添加了一个MyMessage类。

• MyMessage:
  • MyMessage是一个信息类，示例化对象是一条信息，包括type、id、socialValue、Person1、Person2和group等属性，有私发消息和群发消息两种类型。
• MyPerson也添加了socialValue、money和messages等属性；MyNetwork添加了messages属性。

1.3 Homework11

新增了三种信息类型：MyRedEnvelopeMessage、MyNoticeMessage、MyEmojiMssage。

2 性能问题

2.1 容器选择

基本上都选择了速度最快的HashMap容器

例如MyNetwork：

private ArrayList<Person> people = new ArrayList<>();
private HashMap<Integer,Group> groups = new HashMap<>();
private HashMap<Integer,Message> messages = new HashMap<>();
private HashSet<Integer> emojiIdList = new HashSet<>();
private HashMap<Integer,Integer> emojiHeatList = new HashMap<>();
private HashMap<Person,Person> parent = new HashMap<>();
private HashMap<Person,HashSet<Person>> graph = new HashMap<>();

2.2 从dfs到并查集的实现

难点函数是isCircle():本质是查询两个结点之间有没有通路。

我一开始使用的是dfs深度优先搜索的算法，最糟糕的时间复杂度是O(n^2)。后来我优化成了并查集算法。

并查集的本质是通过一个一维数组来维护一个森林。开始时森林中的每一个节点都是孤立的，各自形成一个树。之后，进行若干次的合并操作，每次合并将两个树合并为一个更大的树。

实现方法：

parent保存着结点和它的父节点。

private HashMap<Person,Person> parent;

addRelation()函数中：

添加而父结点的关系。

	if (parent.get(getPerson(id1)) == null && parent.get(getPerson(id2)) == null) {
 		parent.put(getRoot(getPerson(id1)),getRoot(getPerson(id2)));
	} else if (parent.get(getPerson(id1)) == null) {
 		if (!getRoot(getPerson(id2)).equals(getPerson(id1))) {
			parent.put(getPerson(id1),getRoot(getPerson(id2)));
    	}
	} else if (parent.get(getPerson(id2)) == null) {
    	if (!getRoot(getPerson(id1)).equals(getPerson(id2))) {
        	parent.put(getPerson(id2),getRoot(getPerson(id1)));
    	}
	} else {
    	if (!getRoot(getPerson(id1)).equals(getRoot(getPerson(id2)))) {
        	parent.put(getRoot(getPerson(id1)),getRoot(getPerson(id2)));
   		}
	}

采用getRoot()函数进行查询操作，判断其父结点是不是一致的，如果一致两个结点之间就存在路径，即isCircle()返回值是true：

在查询过程中会有路径压缩操作。

   public Person getRoot(Person person) {
        Person root = person;
        while (parent.get(root) != null) {
            root = parent.get(root);
        }
        return root;
    }

2.3 krustal算法

难点函数是queryLeastConnection(int id):本质是找到和id联通的最大点集，构造该点集的最小生成树。我使用了krustal算法。

Krustal算法查找最小生成树的方法是：将连通网中所有的边按照权值大小做升序排序，从权值最小的边开始选择，只要此边不和已选择的边一起构成环路，就可以选择它组成最小生成树。对于 N 个顶点的连通网，挑选出 N-1 条符合条件的边，这些边组成的生成树就是最小生成树。

2.4 Dijkstra堆优化算法

难点函数是sendIndirectMessage()：本质是查询两个结点之间的最短路径。

Dijkstra算法详解：先建立一个dist数组表示和起点相连的各个点之间的最小值，先加入起点及其相连的点之间的距离，其他的赋值为inf（无穷大），开始在dist数组中扫描到距离最小的点，将其标记如最小生成树中，再看是否可以对其他点进行松弛操作；一直重复到所有点全部被标记结束。操作完之后dist[i]中存的就是和起点到 i 点的最小值。

部分实现代码：

public int main() {
	Person nextPerson;
	nextPerson = this.person1;
	while (!(nextPerson.equals(person2))) {
		int weight = minHeapWeight.get(1);
        Person person = this.get();
        while (flag.get(person.getId())) {
            weight = minHeapWeight.get(1);
            person = this.get();
        }
        this.flag.put(person.getId(),true);
        this.path.put(person,weight);
        //更新距离
        for (Person peo : graph.get(person)) {
			if (!this.path.containsKey(peo)) {
				this.add(peo,peo.queryValue(person) + this.path.get(person));
				this.path.put(peo,peo.queryValue(person) + this.path.get(person));
			} else if (this.path.get(peo) > peo.queryValue(person) + this.path.get(person)) {
				this.add(peo,peo.queryValue(person) + this.path.get(person));
			}
		}
		nextPerson = person;
    }
	return path.get(person2);
}

2.5 动态维护

实现函数为queryGroupValueSum():

在MyGroup类中：

private int valueSum;

public void addPerson(Person person) {
	if (!this.hasPerson(person)) {
		for (Integer id:people.keySet()) {
			valueSum = valueSum + (people.get(id).queryValue(person) * 2);
        }
        this.ageSum += person.getAge();
        people.put(person.getId(),person);
	}
}

在查询的时候直接返回valueSum即可

@Override
public int getValueSum() {
	return this.valueSum;
}

3 bug修复情况

3.1 Homework9

这次作业完成的比较仓促，所以由有两个bug：

1. 并查集在添加parent结点的时候没有考虑到本身就是最顶层节点的情况，所以会导致在并查集查询的时候出现死循环tle的情况。
2. 纯属手误，输出信息打错了。（汗流光了

3.2 Homework10

这次作业主要问题是性能问题：

将一些变量查询方法改为动态维护之后节省了很多时间，就不tle了。

3.3 Homework11

Dijkstra堆优化算法有一个小bug，导致有一个点tle。

4 测试数据准备

集中测试：

• 在输入了基础信息之后，可以构造同一个查询指令很多条，这样可以查出来是否有超时现象出现，是否需要优化。

边缘数据：

• 比如group的人数上限1111，getReceivedMessage()的条数为4条

构造异常数据：

• 除了正常输出的情况之外，异常类的测试也是很有必要的。可以验证异常类的判定是否正确。

5 Network扩展任务

假设出现了几种不同的Person

• Advertiser：持续向外发送产品广告
• Producer：产品生产商，通过Advertiser来销售产品
• Customer：消费者，会关注广告并选择和自己偏好匹配的产品来购买 -- 所谓购买，就是直接通过Advertiser给相应Producer发一个购买消息
• Person：吃瓜群众，不发广告，不买东西，不卖东西

如此Network可以支持市场营销，并能查询某种商品的销售额和销售路径等 请讨论如何对Network扩展，给出相关接口方法，并选择3个核心业务功能的接口方法撰写JML规格（借鉴所总结的JML规格模式）

• 新建Advertiser、Producer和Customer类继承Person类。
  • 对于Producer内部会有一个products数组保存当前有的产品product。
• 新建Product类，内含有id，value等信息。
• 在Network中添加products[]、advertisers[]、Producers[]、Customers[]、purchaseMessages[]。

addProduct(Product product)：添加产品

/*@ public normal_behavior
      @ requires !(\exists int i; 0 <= i && i < products.length; peoducts[i].equals(product));
      @ assignable products;
      @ ensures products.length == \old(products.length) + 1;
      @ ensures (\forall int i; 0 <= i && i < \old(products.length);
      @          (\exists int j; 0 <= j && j < products.length; products[j] == (\old(products[i]))));
      @ ensures (\exists int i; 0 <= i && i < products.length; products[i] == product);
      @ also
      @ public exceptional_behavior
      @ signals (EqualProductIdException e) (\exists int i; 0 <= i && i < products.length;
      @                                     products[i].equals(product));
      @*/
    public void addProduct(/*@ non_null @*/Product product) throws EqualProductIdException;

queryProductValue(Product product):查询商品的value

/*@ public normal_behavior
      @ requires (\exists int i; 0 <= i && i < products.length; 
      @          products[i].getId() == product.getId());
      @ assignable \nothing;
      @ ensures (\exists int i; 0 <= i && i < products.length; 
      @         products[i].getId() == product.getId() && \result == value[i]);
      @ also
      @ public normal_behavior
      @ requires (\forall int i; 0 <= i && i < products.length; 
      @          products[i].getId() != product.getId());
      @ ensures \result == 0;
      @*/
    public /*@ pure @*/ int queryProductValue(Product product);

sendPurchaseMessage():Customer直接通过Advertiser给相应Producer发一个购买消息

/*@ public normal_behavior
  @ requires containsPurchaseMessage(id);
  @ assignable purchaseMessages;
  @ assignable people[*].purchaseMessages;
  @ ensures !containsPurchaseMessage(id) && purchaseMessages.length == \old(purchaseMessages.length) - 1 &&
  @         (\forall int i; 0 <= i && i < \old(purchaseMessages.length) && \old(purchaseMessages[i].getId()) != id;
  @         (\exists int j; 0 <= j && j < purchaseMessages.length; purchaseMessages[j].equals(\old(purchaseMessages[i]))));
  @ ensures (\forall int i; 0 <= i && i < people.length; person[i].likeType(\old(((PurchaseMessage)getMessage(id))).getType) ==> 
  @         ((\forall int j; 0 <= j && j < \old(person[i].getMessages().size());
  @          person[i].getMessages().get(j+1) == \old(person[i].getMessages().get(j))) &&
  @         (person[i].getMessages().get(0).equals(\old(getMessage(id)))) &&
  @         (person[i].getMessages().size() == \old(person[i].getMessages().size()) + 1)));
  @ also
  @ public exceptional_behavior
  @ signals (MessageIdNotFoundException e) !containsPurchaseMessage(id);
  @*/
public /*@ pure @*/ void sendPurchaseMessage(int id) throws PurchseMessageIdNotFoundException;

6 本单元学习体会

• 本单元的学习相比于第二单元就显得很仓促。一开始就没太明白这个单元要让我们做什么，后来再和同学交流的过程中勉勉强强了解了，却鲜有自己的想法，导致后面的实现有一点点坎坷。
• 这个单元比较考验耐心。相比于自己实现函数，这个单元我们先要阅读JML语言，然后满足其描述的条件下，写函数。如果没有很耐心地读完JML描述，就无法正确地完成功能。这个单元的作业个人感觉没有上个单元认真，没有做好足够强的课下测试，导致我出现了很多bug。（痛心疾首
• 个人在前两个单元对性能都比较佛系，在这个单元就很吃亏，在每一个函数实现的过程中，都会强迫自己去想最优的算法，而不是抱以“实现了就万事大吉”的错误观念。这个单元的学习也推动我去寻找最优解的想法、如何让自己的性能尽可能好，这是我前两个单元都忽略了的地方。
• 这个单元对我而言意义很重大，它培养了我“优化”的思想，而不是拘泥于现状。
• 希望在终章的实现中，我可以做得更好！