红黑树~
ref: 《STL源码剖析》
红黑树
红黑树是一种平衡二叉树;平衡二叉树有AVL-TREE、RB-TREE、AA-TREE等;
“平衡”的大致意思是:没有任何一个节点过深。
此外,红黑树还必须满足以下规则:
- 每个节点不是红色就是黑色;
- 根节点为黑色;
- 如果节点为红色,其子节点必须为黑色;
- 任一节点至NULL(树尾端,叶节点的子节点)的任何路径,所含黑节点数必须相同;
插入
首先需要将新节点插入树中,将其设置为红色,然后重新平衡(rebalance);
template <class Key, class Value, class KeyOfValue, class Compare>
pair <typename rb_tree<Key, Value, KeyOfValue, Compare>::iterator, bool> rb_tree<Key, Value, KeyOfValue, Compare>::insert_unique(const Value &v){ // 插入唯一的值
link_type y = header;
// 从树根开始遍历,找到合适的插入位置;
link_type x = root();
bool cmp = true;
while( x != 0 ){
y = x;
cmp = key_compare(KeyOfValue()(v), key(x)); // key_compare 等价于 key(v) < key(x)
x = cmp ? left(x) : right(x); // 小于向左,大于等于向右
}
// 结束循环时,y为x的父节点
iterator it = iterator(y);
if(cmp) // cmp 为最后一次比较的结果
if(it == begin()) // 如果插入点为最左节点,直接插入
return pair<iterator, bool>(_insert(x, y, v), true);
else // 否则,it--
it--;
if(key_compare(key(it.node_ptr), KeyOfValue()(v)))
return pair<iterator, bool>(_insert(x, y, v), true);
// 这样做的原因是,最后,插入点假设为ite,则满足:*(ite-1) < *ite < *(ite+1);
// 但如果找到的位置不满足这个关系,则必然已经有该值
return pair<iterator, bool>(it, false);
}
template <class Key, class Value, class KeyOfValue, class Compare>
typename rb_tree<Key, Value, KeyOfValue, Compare>::iterator
rb_tree<Key, Value, KeyOfValue, Compare>::_insert(base_ptr_type x, base_ptr_type y, const value_type &v){
// 插入点为x,x的父节点为y,v为插入的值
link_type _x = (link_type)x;
link_type _y = (link_type)y;
link_type z;
if(_y == header || _x != 0 || key_compare(KeyOfValue()(v), key(_y))){
z = create_node(v);
left(_y) = z;
if(_y == header){
root() = z;
rightmost() = z;
}
else if(_y == leftmost()){
leftmost() = z;
}
}
else{
z = create_node(v);
right(_y) = z;
if(_y == rightmost())
rightmost() = z;
}
parent(z) = _y;
left(z) = 0;
right(z) = 0;
_rb_tree_rebalance(z, header->parent); // 重新平衡
node_count ++;
return iterator(z);
}
根据条件4,所有新节点必须为红色,根据条件3,新节点之父必须为黑,如果上述两个条件未能满足,则需要改变树的形状。
假定:
插入的元素:X
X的父节点:P
P的父节点:G
P的兄弟节点:S
G的父节点:GG
X必然为红色,此时对于插入有以下几种情况:
P为黑色
直接插入即可(下图,40节点插入45)
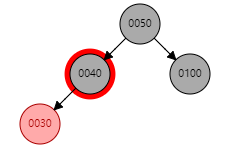
P为红色
这就复杂了啊,还需要几种情况讨论:
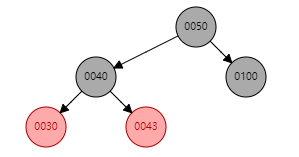
1. S为黑且X为外侧插入:单旋
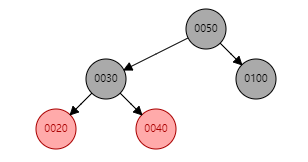
// 左旋
inline void _rb_tree_rotate_left(rb_tree_base_node *x, rb_tree_base_node* &root){
rb_tree_base_node *y = x->right;
x->right = y->left;
if(y->left){
y->left->parent = x;
}
y->parent = x->parent;
if(x == root){
root = y;
}
else if(x == x->parent->left){
x->parent->left = y;
}
else{
x->parent->right = y;
}
y->left = x;
x->parent = y;
}
// 右旋
inline void _rb_tree_rotate_right(rb_tree_base_node *x, rb_tree_base_node* &root){
rb_tree_base_node *y = x->left;
x->left = y->right;
if(y->right){
y->right->parent = x;
}
y->parent = x->parent;
if(x == root){
root = y;
}
else if(x == x->parent->right){
x->parent->right = y;
}
else{
x->parent->left = y;
}
y->right = x;
x->parent = y;
}
2. S为黑且X为内侧插入:双旋
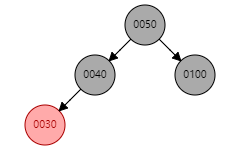
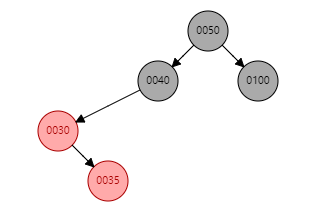
先进行一次单旋
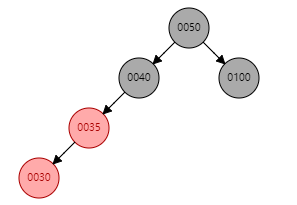
此时,相当于上一种情况,再次单旋
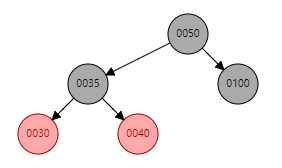
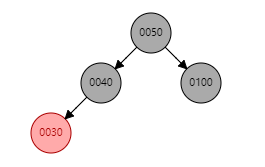
3. S为红色且X为外(内)侧插入:单旋(也可以直接变色)
之后有两种结果,一种为GG为黑色(如下图所示,则直接返回即可);另一种为GG为红色,则需要继续处理(见4);
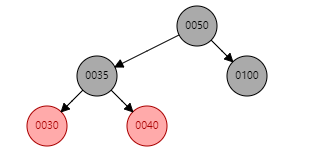
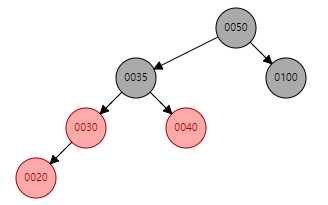
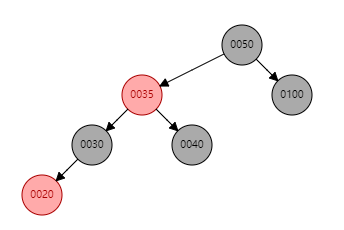
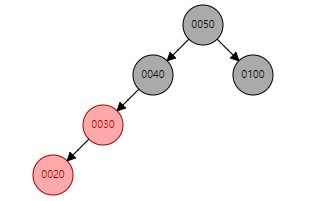
4. S为红色且X为外(内)侧插入(续)
这时,可以将G设为X,那么此时问题又转化了之前的状况,以此循环;
重平衡代码实现:
inline void _rb_tree_rebalance(rb_tree_base_node* x, rb_tree_base_node* &root){
x->color = rb_tree_color_red; // 新节点必须为红色
while(x != root && x->parent->color == rb_tree_color_red){ // 父节点需要为红色
if(x->parent == x->parent->parent->left){ // X在GG的左子树
rb_tree_base_node *y = x->parent->parent->right; // Y为S
if(y && y->color == rb_tree_color_red){ // S为红色,只需要变色(3)
x->parent->color = rb_tree_color_black;
y->color = rb_tree_color_black;
x->parent->parent->color = rb_tree_color_red;
x = x->parent->parent; // X变为GG,继续循环(4)
}
else{
if(x == x->parent->right){ // 如果在内侧,两次旋转(2)
x = x->parent;
_rb_tree_rotate_left(x, root);
} // 如果在外侧,只需要单旋(1)
x->parent->color = rb_tree_color_black;
x->parent->parent->color = rb_tree_color_red;
_rb_tree_rotate_right(x->parent->parent, root);
}
}
else{ // 与上一个类似
rb_tree_base_node *y = x->parent->parent->left;
if(y && y->color == rb_tree_color_red){
x->parent->color = rb_tree_color_black;
y->color = rb_tree_color_black;
x->parent->parent->color = rb_tree_color_red;
x = x->parent->parent;
}
else{
if(x == x->parent->left){
x = x->parent;
_rb_tree_rotate_right(x, root);
}
x->parent->color = rb_tree_color_black;
x->parent->parent->color = rb_tree_color_red;
_rb_tree_rotate_left(x->parent->parent, root);
}
}
}
root->color = rb_tree_color_black; // 确保根节点为黑色
}
完整代码
#ifndef RBTREE
#define RBTREE
#include <utility>
#include <iostream>
#include <typeinfo>
using namespace std;
typedef bool rb_tree_color_type;
const rb_tree_color_type rb_tree_color_red = false;
const rb_tree_color_type rb_tree_color_black = true;
struct rb_tree_base_node{
typedef rb_tree_color_type color_type;
typedef rb_tree_base_node * link_type;
color_type color;
link_type parent;
link_type left;
link_type right;
static link_type minimum(link_type x){
while (x->left != 0) x = x->left;
return x;
}
static link_type maximum(link_type x){
while (x->right != 0) x = x->right;
return x;
}
};
template <class Value>
struct rb_tree_node: public rb_tree_base_node{
typedef rb_tree_node<Value> *link_type;
Value value_field;
};
struct rb_tree_iterator_base{
rb_tree_base_node *node_ptr;
void increment();
void decrement();
};
template <class Value,class Ref,class Ptr>
struct rb_tree_iterator: public rb_tree_iterator_base{
typedef Value value_type;
typedef Ref reference;
typedef Ptr pointer;
typedef rb_tree_iterator<Value, Value&, Value*> iterator;
typedef rb_tree_iterator<Value, const Value&, const Value*> const_iterator;
typedef rb_tree_iterator<Value, Ref, Ptr> self;
typedef rb_tree_node<Value> *link_type;
rb_tree_iterator(){}
rb_tree_iterator(link_type x){ node_ptr = x; }
rb_tree_iterator(const iterator &it){ node_ptr = it.node_ptr; }
reference operator*() const { return link_type(node_ptr)->value_field; }
pointer operator->() const { return &(operator*()); }
self &operator++(){ increment(); return *this;}
self operator++(int){
self tmp = *this;
increment();
return tmp;
}
self &operator--(){ decrement(); return *this;}
self operator--(int){
self tmp = *this;
decrement();
return tmp;
}
bool operator==(const iterator &it) const{
return (operator*()) == (*it);
}
};
// template <class Key, class Value, class KeyOfValue, class Compare, class Alloc = alloc>
template <class Key, class Value, class KeyOfValue, class Compare>
class rb_tree{
protected:
typedef void* void_pointer;
typedef rb_tree_base_node *base_ptr_type;
typedef rb_tree_node<Value> rb_tree_node_type;
// typedef simple_alloc<rb_tree_node_type, Alloc> rb_tree_node_allocator;
typedef rb_tree_color_type color_type;
public:
typedef Key key_type;
typedef Value value_type;
typedef value_type *pointer;
typedef const value_type* const_pointer;
typedef value_type &reference;
typedef const value_type &const_reference;
typedef rb_tree_node_type *link_type;
typedef size_t size_type;
typedef ptrdiff_t difference_type;
protected:
// link_type get_node() { /* TO-DO */ }
// void put_node(link_type p) { /* TO-DO */ }
link_type create_node(const value_type& x){
link_type tmp = new rb_tree_node<value_type>();
tmp->value_field = x;
return tmp;
}
link_type clone_node(link_type x){
link_type tmp = create_node(x->value_field);
tmp->color = x->color;
tmp->left = 0;
tmp->right = 0;
return tmp;
}
void destroy_node(link_type p){
delete &(p->value_field);
delete p;
}
protected:
size_type node_count;
link_type header;
Compare key_compare;
link_type &root() const{
return (link_type &)(header->parent);
}
link_type &leftmost() const{
return (link_type &)(header->left);
}
link_type &rightmost() const{
return (link_type &)(header->right);
}
static link_type &left(link_type x){
return (link_type &)(x->left);
}
static link_type &right(link_type x){
return (link_type &)(x->right);
}
static link_type &parent(link_type x){
return (link_type &)(x->parent);
}
static reference value(link_type x){
return x->value_field;
}
static const key_type &key(link_type x){
return KeyOfValue()(value(x)); // KeyOfValue 仿函数,用于从实值value中取出键值key, (用户定义并传入的)
}
static color_type &color(link_type x){
return (color_type &)(x->color);
}
static link_type &left(base_ptr_type x){
return (link_type &)(x->left);
}
static link_type &right(base_ptr_type x){
return (link_type &)(x->right);
}
static link_type &parent(base_ptr_type x){
return (link_type &)(x->parent);
}
static reference value(base_ptr_type x){
return ((link_type)x)->value_field;
}
static const key_type &key(base_ptr_type x){
return KeyOfValue()(value((link_type)x)); // KeyOfValue 仿函数,用于从实值value中取出键值key, (用户定义并传入的)
}
static color_type &color(base_ptr_type x){
return (color_type &)((link_type)x->color);
}
static link_type minimum(link_type x){
return (link_type) rb_tree_base_node::minimum(x);
}
static link_type maximum(link_type x){
return (link_type) rb_tree_base_node::maximum(x);
}
public:
typedef rb_tree_iterator<value_type, reference, pointer> iterator;
private:
iterator _insert(base_ptr_type x, base_ptr_type y, const value_type &v); // 插入点为x,父节点为y,参数v为新值,即插入在x和y之间
link_type _copy(link_type, link_type);
void _erase(link_type);
void init(){
header = new rb_tree_node<Value>();
color(header) = rb_tree_color_red;
root() = 0;
leftmost() = header;
rightmost() = header;
}
public:
rb_tree(const Compare& comp = Compare()): node_count(0), key_compare(comp) {
init();
}
~rb_tree(){
// clear();
delete header;
}
rb_tree<Key, Value, KeyOfValue, Compare> & operator=(const rb_tree<Key, Value, KeyOfValue, Compare>);
public:
Compare key_comp() const{return key_compare;}
iterator begin(){ return leftmost();}
iterator end(){ return header;}
bool empty()const{ return node_count == 0; }
size_type size() const{ return node_count; }
size_type max_size() const{ return size_type(-1); }
public:
pair<iterator, bool> insert_unique(const value_type&);
template<class InputIterator>
void insert_unique(const InputIterator&, const InputIterator&);
iterator insert_equal(const value_type&);
template<class InputIterator>
void insert_equal(const InputIterator&, const InputIterator&);
iterator find(const Key &k);
};
inline void _rb_tree_rotate_left(rb_tree_base_node *x, rb_tree_base_node* &root){
rb_tree_base_node *y = x->right;
x->right = y->left;
if(y->left){
y->left->parent = x;
}
y->parent = x->parent;
if(x == root){
root = y;
}
else if(x == x->parent->left){
x->parent->left = y;
}
else{
x->parent->right = y;
}
y->left = x;
x->parent = y;
}
inline void _rb_tree_rotate_right(rb_tree_base_node *x, rb_tree_base_node* &root){
rb_tree_base_node *y = x->left;
x->left = y->right;
if(y->right){
y->right->parent = x;
}
y->parent = x->parent;
if(x == root){
root = y;
}
else if(x == x->parent->right){
x->parent->right = y;
}
else{
x->parent->left = y;
}
y->right = x;
x->parent = y;
}
inline void _rb_tree_rebalance(rb_tree_base_node* x, rb_tree_base_node* &root){
x->color = rb_tree_color_red;
while(x != root && x->parent->color == rb_tree_color_red){
if(x->parent == x->parent->parent->left){
rb_tree_base_node *y = x->parent->parent->right;
if(y && y->color == rb_tree_color_red){
x->parent->color = rb_tree_color_black;
y->color = rb_tree_color_black;
x->parent->parent->color = rb_tree_color_red;
x = x->parent->parent;
}
else{
if(x == x->parent->right){
x = x->parent;
_rb_tree_rotate_left(x, root);
}
x->parent->color = rb_tree_color_black;
x->parent->parent->color = rb_tree_color_red;
_rb_tree_rotate_right(x->parent->parent, root);
}
}
else{
rb_tree_base_node *y = x->parent->parent->left;
if(y && y->color == rb_tree_color_red){
x->parent->color = rb_tree_color_black;
y->color = rb_tree_color_black;
x->parent->parent->color = rb_tree_color_red;
x = x->parent->parent;
}
else{
if(x == x->parent->left){
x = x->parent;
_rb_tree_rotate_right(x, root);
}
x->parent->color = rb_tree_color_black;
x->parent->parent->color = rb_tree_color_red;
_rb_tree_rotate_left(x->parent->parent, root);
}
}
}
root->color = rb_tree_color_black;
}
template <class Key, class Value, class KeyOfValue, class Compare>
template <class InputIterator>
void rb_tree<Key, Value, KeyOfValue, Compare>::insert_equal(const InputIterator &first, const InputIterator &last){
InputIterator it = first;
while(it != last){
insert_equal(*it);
it ++;
}
}
template <class Key, class Value, class KeyOfValue, class Compare>
typename rb_tree<Key, Value, KeyOfValue, Compare>::iterator rb_tree<Key, Value, KeyOfValue, Compare>::insert_equal(const Value &v){
link_type y = header;
link_type x = root();
while( x != 0 ){
y = x;
x = key_compare(KeyOfValue()(v), key(x)) ? left(x) : right(x);
}
return _insert(x, y, v);
}
template <class Key, class Value, class KeyOfValue, class Compare>
template <class InputIterator>
void rb_tree<Key, Value, KeyOfValue, Compare>::insert_unique(const InputIterator &first, const InputIterator &last){
InputIterator it = first;
while(it != last){
insert_unique(*it);
it ++;
}
}
template <class Key, class Value, class KeyOfValue, class Compare>
pair <typename rb_tree<Key, Value, KeyOfValue, Compare>::iterator, bool> rb_tree<Key, Value, KeyOfValue, Compare>::insert_unique(const Value &v){
link_type y = header;
link_type x = root();
bool cmp = true;
while( x != 0 ){
y = x;
cmp = key_compare(KeyOfValue()(v), key(x));
x = cmp ? left(x) : right(x);
}
iterator it = iterator(y);
if(cmp)
if(it == begin())
return pair<iterator, bool>(_insert(x, y, v), true);
else
it--;
if(key_compare(key(it.node_ptr), KeyOfValue()(v)))
return pair<iterator, bool>(_insert(x, y, v), true);
return pair<iterator, bool>(it, false);
}
template <class Key, class Value, class KeyOfValue, class Compare>
typename rb_tree<Key, Value, KeyOfValue, Compare>::iterator
rb_tree<Key, Value, KeyOfValue, Compare>::_insert(base_ptr_type x, base_ptr_type y, const value_type &v){
link_type _x = (link_type)x;
link_type _y = (link_type)y;
link_type z;
if(_y == header || _x != 0 || key_compare(KeyOfValue()(v), key(_y))){
z = create_node(v);
left(_y) = z;
if(_y == header){
root() = z;
rightmost() = z;
}
else if(_y == leftmost()){
leftmost() = z;
}
}
else{
z = create_node(v);
right(_y) = z;
if(_y == rightmost())
rightmost() = z;
}
parent(z) = _y;
left(z) = 0;
right(z) = 0;
_rb_tree_rebalance(z, header->parent);
node_count ++;
return iterator(z);
}
template <class Key, class Value, class KeyOfValue, class Compare>
typename rb_tree<Key, Value, KeyOfValue, Compare>::iterator
rb_tree<Key, Value, KeyOfValue, Compare>::find(const Key &k) {
link_type y = header;
link_type x = root();
while(x != 0)
if(!key_compare(key(x), k))
y = x, x = left(x);
else
x = right(x);
iterator it = iterator(y);
return (it == end() || key_compare(k, key(y)))? end() : it;
}
/*
本红黑树有额外的根节点 end/start:
root->parent == end
end->left == minimum
end->right = maximum
*/
void rb_tree_iterator_base::increment(){
if (node_ptr->right != 0){
node_ptr = node_ptr->right;
while(node_ptr->left != 0)
node_ptr = node_ptr->left;
}
else{
rb_tree_base_node *p = node_ptr->parent;
if(p->right == node_ptr){
p = p->parent;
node_ptr = node_ptr->parent;
while(p->right == node_ptr){
p = p->parent;
node_ptr = node_ptr->parent;
}
}
if(p->right != node_ptr) //不满足该条件则指向了end
node_ptr = p;
}
}
void rb_tree_iterator_base::decrement(){
if (node_ptr->left != 0){
node_ptr = node_ptr->left;
}
else{
rb_tree_base_node *p = node_ptr->parent;
if(p->right == node_ptr){
node_ptr = p;
}
else{
node_ptr = p;
p = node_ptr->parent;
while(p->left == node_ptr){
node_ptr = p;
p = node_ptr->parent;
}
if(p->right == node_ptr)
node_ptr = p;
}
}
}
#endif
set
特性
1)所有元素都会根据键值自动排序;
2)set元素的键值就是实值,实值就是键值;
3)set不允许两个元素有相同的键值;
4)不可以通过迭代器改变set元素值,因为set元素值就是键值,如果任意改变set元素值,会严重破坏set组织(故set
实现
set以RB-tree为底层机制,set几乎只是转调用RB-tree的操作行为;
我们在红黑树实现的时候,其实k,v都存储于Value中,然后通过KeyOfValue仿函数,从实值value中取出键值key,如set的Value就是key,而map的Value为pair<key, value> (用户定义并传入的)
1.类型定义
template<class Key, class Compare=less<Key>>
class set{
public:
typedef Key key_type;
typedef Key value_type;
private:
typedef rb_tree<key_type, value_type, identity<value_type>, key_compare> rep_type;
// 上述四个模板参数分别为:键值类型、实值类型、获取键值的方法、键值的比较方法
rep_type t; // 定义了一个红黑树。。。。
// 下面是 identity<value_type> 定义
template <class T>
struct identiry : public unary_function<T, T> { // 由于set键值就是实值,
// 我们只需要通过该函数取出value的值即可
const T&operator()(const T& x) const {return x;}
};
public:
typedef typename rep_type::const_iterator iterator; // 注意是const
};
2.其他实现
pair<iteartor, bool> insert(const value_type& x){ // 注意:因为元素不可重复,所以使用insert_unique(调用RB_tree::insert_unique)
pair<typename rep_type::iterator, bool> p = t.insert_unique(x);
return pair<iterator, bool>(p.first, p.second);
}
map
特性:
1)所有元素都会根据元素的键值自动被排序;
2)所有元素都是pair,同时拥有实值(value)和键值(key),pair的第一元素被视为键值,第二元素被视为实值;
3)map不允许两个元素拥有相同的键值;
4)不能通过迭代器改变map的键值,但可以改变实值
// pair定义
template <class T1, class T2>
struct pair{
typedef T1 first_type;
typedef T2 second_type;
T1 first;
T2 second;
pair() : first(T1()), second(T2()) { }
pair(const T1& a, const T2& b): first(a), second(b) {}
};
实现
1. 类型定义
template<class Key, class T, class Compare=less<Key>>
class map{
public:
// Key -- 键值类别 T -- 实值类型
typedef Key key_type;
typedef T data_type;
typedef pair<const Key, T> value_type; // 注意:是const Key,说明键值无法修改,但实值可以
// 仿函数,用于比较元素
class value_compare :public binary_function<value_type, value_type, bool> {
friend class map<Key, T, Compare>;
protected:
Compare comp;
value_compare(Compare c) :comp(c)
public:
bool operator()(const value_type& x, const value_type& y) const {
return comp(x.first, y.first);
}
};
private:
// 使用红黑树表示map, select1st<value>(pair<key, value>)取出pair中的key
typedef rb_tree<key_type, value_type, select1st<value>, key_compare> rep_type;
rep_type t;
public:
typedef typename rep_type::iterator iterator; // 注意,和set不同,这里的iterator并不是const,应为允许用户修改迭代器的实值;
};
2. 其他实现
// 插入,和set一样,调用的insert_unique
pair<iterator, bool> insert(const value_type& x){
return t.insert_unique(x);
}
// 下标操作符map[k],试图向map中插入pair(k, v());(v():初始化一个默认的value)
// 如果没有k,则直接插入,并返回v()的引用;
// 如果有k,则返回则返回找到的*(pair<iterator,bool>.first).second引用;(参照insert_unique的返回值)
T& operator[](const key_type& k){
return (*(insert(value_type(k, T())).first)).second;
}
multiset和multimap
他们和map、set的唯一区别是他们insert调用的是RB_tree::insert_equal而非RB_tree::insert_unique;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号