图像压缩与离散余弦变换

把图像看作如100x100个点(像素)，每个像素红绿蓝3个灯泡，是直观的。

RGB可以转换成YUV亮度和颜色。YUV和RGB来回转换不丢失信息，也不能压缩。人眼对亮度比对颜色敏感，比如灯光昏暗时分辨不出颜色。每2个或4个点共用颜色信息，如(100, 101, 98, 99)用100来表示，就可以压缩图像(和损失质量)。

YUV三个平面plane，都是数，比如用0到255的整数来表示。对它们的处理方式是一样的。8x8的块/二维数组，每个数组元素都是Y或U或V。把二维数组压扁成一个8x8=64的一维数组，y轴表示亮度Y(U和V的处理方式一样)，x轴表示0~63 (row*8 + column)，就可以画出个波形，或者说图像变成了信号。

把一堆频率/周期不同的正弦波叠加起来，sin(x)前乘的系数不同，只要正弦波的数量足够多，就可以叠加出任意波形。0~63的变化是不连续的，如x轴上没有1.6, 2.7这样的点。正弦曲线平移可得到余弦曲线，于是有了离散余弦变换。x轴是时间y轴是音量时，"时域到频域的变换"非常贴切。信号处理是比图像处理更广泛的概念。

离散余弦变换和Inverse离散余弦变换类似于RGB和YUV互转，也是无损失无压缩的。压缩靠对频率不同的分量信号使用不同的量化级数。0,1,2,3,都用0代替，4,5,6,7,都用1代替是量化的一个例子。量化得"越狠"，压缩比就越高。如极端例子都是0，用64和0两个数即可表示/传输/记录64个0。0~63都出现了，又没有规律，就不好压缩了。

cos(4x)比cos(x)的频率高，周期短，波形变化得快，cos(4x)的[0, pi/2]相当于cos(x)的[0, 2*pi]。

比如有张美人脸的图片 :-)。脸蛋的颜色是直流分量，频率最低。腮红是频率比直流高的分量。高频分量么，眼线笔描变眼影刷涂，不细看注意不到，高频分量狠狠地量化，就可以压缩图像了。好像还得之字形排列一下，才容易出来连续的0，而不是0 1 0 1 0 0 之类。

胡说完了八道：64个输入，可以固定用64个频率不同的cosine，高频的丢掉。每个cosine的系数是未知数，把每个点代入，得到64个64元一次方程。反向离散余弦变换IDCT也是乘来加去。并不是TPU就比CPU厉害了，TPU做除法运算吗？CPU是通用的。说点正经的：

Like the discrete Fourier transform (DFT), a DCT operates on a function at a finite number of discrete data points. The obvious distinction between a DCT and a DFT is that the former uses only cosine functions, while the latter uses both cosines and sines (in the form of complex exponentials).

... lead to all the standard variations of DCTs and also discrete sine transforms (DSTs).

The most common variant of discrete cosine transform is the type-II DCT, which is often called simply "the DCT". This was the original DCT as first proposed by Ahmed. Its inverse, the type-III DCT, is correspondingly often called simply "the inverse DCT" or "the IDCT".

Using the normalization conventions above, the inverse of DCT-I is DCT-I multiplied by 2/(N-1). The inverse of DCT-IV is DCT-IV multiplied by 2/N. The inverse of DCT-II is DCT-III multiplied by 2/N and vice versa.

 

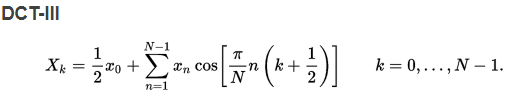
我推了下N=1的情况:-)。DCT-II出来的x₀是所有x_n的和，再除以N就是均值。也许可以说x₀是总代表，x_k围绕着x₀交替。

from math import *
import numpy as np
N = 3
dm = np.ndarray(shape=(N, N)) # DCT matrix
im = np.ndarray(shape=(N, N)) # IDCT matrix
for k in range(N):
    for n in range(N):
        dm[n][k]  = cos(pi / N * (n + 0.5) * k)
        im[n][k] = cos((pi / N) * n * (k + 0.5)) if n > 0 else 0.5
a = [10] * N; b = np.matmul(a, dm); c = np.matmul(b, im)
np.set_printoptions(precision=5, suppress=True) # 不使用科学计数法
print(f'{dm=}', f'{im=}', sep='\n')
print(f'{a=}', f'{b=}', f'{c=}', sep='\n')
print('dm * im =', np.matmul(dm, im))
'''
dm=array([[ 1.     ,  0.86603,  0.5    ],
       [ 1.     ,  0.     , -1.     ],
       [ 1.     , -0.86603,  0.5    ]])
im=array([[ 0.5    ,  0.5    ,  0.5    ],
       [ 0.86603,  0.     , -0.86603],
       [ 0.5    , -1.     ,  0.5    ]])
a=[10, 10, 10]
b=array([30.,  0., -0.])
c=array([15., 15., 15.])
dm * im = [[ 1.5 -0.  -0. ]
 [-0.   1.5  0. ]
 [-0.   0.   1.5]]
'''
# 注意*和matmul不一样。https://blog.csdn.net/u012300744/article/details/80423135

Fast discrete cosine transform algorithms (nayuki.io)   FFmpeg: libavcodec/x86/idct_sse2_xvid.c Source File

AVS2——第二代AVS标准 全文没有出现"智能"俩字。窃以为："智能"被滥用了，听到"智能"我的第一反应是"马桶":-)。图像/语音识别的准确率提高了很多首先是因为计算能力大大提高了。搞人工智能的数学不如搞视频编解码的厉害，虽然都比我厉害很多。搞航天的可能比搞视频编解码的又厉害一些。

为啥那一堆cosine乘来加去能出来个单位阵*N/2? 好像可以用到倍角公式cos(2x)=2cos²(x) - 1. 还有cos(x+2*pi)=cos(x). 生成dm和im时可以放(n+0.5)*k和n*(k+0.5)来观察下。

不知能否用类似的方法压缩AI用的参数矩阵。比如每2x2的块用均值代替(均值有很多种)，每8x8的块来个DCT(到使用频率域:-)的转换)。每个参数用16位float的方法感觉有点糙快猛。