angle

In Euclidean geometry [欧氏几何], an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex [顶点] of the angle. Angles formed by two rays lie in the plane that contains the rays. Angles are also formed by the intersection of two planes [两个平面相交]. These are called dihedral angles. Two intersecting curves define also an angle, which is the angle of the tangents [切线] at the intersection point. For example, the spherical angle [球面角] formed by two great circles on a sphere equals the dihedral angle between the planes containing the great circles.

Angles smaller than a right angle (less than 90°) are called acute angles ("acute" meaning "sharp"). An angle equal to 90° or π/2 radians is called a right angle. Two lines that form a right angle are said to be normal, orthogonal, or perpendicular. Angles larger than a right angle and smaller than a straight angle [平角] (between 90° and 180°) are called obtuse angles ("obtuse" meaning "blunt"). An angle equal to 180° or π radians is called a straight angle.

The term normal in mathematics is used in the following broad senses:
1. To denote something upright or perpendicular [指sth竖直或垂直]
2. To denote something that is as it should be. In this sense, normal means good or desirable rather than typical
法线(normal line)指始终垂直于某平面的直线。正态分布(Normal distribution)也叫常态分布或高斯分布(Gaussian distribution)。

A reference angle is the acute version of any angle determined by repeatedly subtracting or adding straight angle, to the results as necessary, until the magnitude of the result is an acute angle, a value between 0 and 90°. For example, an angle of 30 degrees has a reference angle of 30 degrees, and an angle of 150 degrees also has a reference angle of 30 degrees (180–150). An angle of 750 degrees has a reference angle of 30 degrees (750–720).

The two acute angles in a right triangle are complementary [互余]. supplementary angle: 补角。The adjective complementary is from Latin complementum, associated with the verb complere, "to fill up". An acute angle is "filled up" by its complement to form a right angle.

An acute triangle (or acute-angled triangle) is a triangle with three acute angles (less than 90°). An obtuse triangle (or obtuse-angled triangle) is a triangle with one obtuse angle (greater than 90°) and two acute angles.

The grad, also called grade, gradian, or gon, is 1/400 of a turn [周角], so a right angle is 100 grads. The milliradian (mil or mrad) is defined as a thousandth of a radian.

The astronomical [天文学] hour angle is 1/24 of a turn. 1 hour = 15° The minute of arc (or MOA, arcminute, or just minute) is 1/60 of a degree. The second of arc (or arcsecond, or just second) is 1/60 of a minute of arc and 1/3600 of a degree. 3°7′30″ is equal to 3.125 degrees.

In a two-dimensional Cartesian coordinate system [二维笛卡尔坐标系/平面直角坐标系], an angle is typically defined by its two sides, with its vertex at the origin [原点]. The initial side is on the positive x-axis, while the other side or terminal side is defined by the measure from the initial side in radians, degrees, or turns. Positive angles represent rotations toward the positive y-axis and negative angles represent rotations toward the negative y-axis. Positive rotations are anticlockwise [逆时针] and negative rotations are clockwise.

The grade of a slope, or gradient is equal to the tangent of the angle, or sometimes (rarely) the sine. A gradient is often expressed as a percentage. For very small values (less than 5%), the grade of a slope is approximately the measure of the angle in radians.

In the Euclidean space, the angle θ between two Euclidean vectors u and v is related to their dot product and their lengths by the formula:

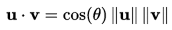
In mathematics, the dot product or scalar product [点积或标量积] is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called "the" inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space. 总结:点积是一种内积。:-)

六级/考研单词: geometry, ray, junction, curve, sphere, acute, norm, blunt, mathematics, denote, upright, desire, subtract, necessity, magnitude, triangle, complement, adjective, verb, astronomy, arc, coordinate, terminal, rotate, clockwise, seldom, algebra, outer