Factorization

Factorization or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kind. For example, 3 × 5 is a factorization of the integer 15, and (x – 2)(x + 2) is a factorization of the polynomial x^2 – 4. Matrices possess many kinds of matrix factorizations.

Although integer factorization is a sort of inverse to multiplication, it is much more difficult algorithmically, a fact which is exploited in the RSA cryptosystem to implement public-key cryptography. Pierre de Fermat was unable to discover that the 6th Fermat number 1 + 2^32 is not a prime number.

log(2)=0.3, 20位二进制约6位六进制，32位10位，64位19位, 128位38位。两个8位二进制数相乘，可写成(a*16+b)*(c*16+b)=ac*256+bc*16*ab+bb. *256放在另一个寄存器里，*16分成两截，ab和bb各最多8位。

Manipulating expressions is the basis of algebra. Factorization is one of the most important methods for expression manipulation for several reasons. If one can put an equation in a factored form E*F = 0, then the problem of solving the equation splits into two independent (and generally easier) problems E = 0 and F = 0. When an expression can be factored, the factors are often much simpler, and may thus offer some insight on the problem. But factorization is not always possible, and when it is possible, the factors are not always simpler. For example, x^10 - 1 = (x-1)*(x^9 + x^8 + ... + x + 1).

The first polynomial factorization algorithm was published by Theodor von Schubert in 1793. Leopold Kronecker rediscovered Schubert's algorithm in 1882 and extended it to multivariate polynomials and coefficients in an algebraic extension. But most of the knowledge on this topic is not older than circa 1965 and the first computer algebra systems: When the long-known finite step algorithms were first put on computers, they turned out to be highly inefficient. The fact that almost any uni- or multivariate polynomial of degree up to 100 and with coefficients of a moderate size (up to 100 bits) can be factored by modern algorithms in a few minutes of computer time indicates how successfully this problem has been attacked during the past fifteen years. (Erich Kaltofen, 1982) Nowadays, modern algorithms and computers can quickly factor univariate polynomials of degree more than 1000 having coefficients with thousands of digits. 1000位十进制数有3322个二进制位。量子计算是质变，8个4096位寄存器，baremetal能且仅能分解整数是小量变。我是外行，我不知道4096根线现实不。

Yun, David Y.Y. (1976). On square-free decomposition algorithms SYMSAC '76 Proceedings of the third ACM symposium on Symbolic and algebraic computation, pp. 26–35.

Berlekamp's algorithm is a well-known method for factoring polynomials over finite fields (also known as Galois fields). The algorithm consists mainly of matrix reduction and polynomial GCD computations. It was invented by Elwyn Berlekamp in 1967. It was the dominant algorithm for solving the problem until the Cantor–Zassenhaus algorithm of 1981. It is currently implemented in many well-known computer algebra systems.

没有一目了然的。search(github emcd123 PolynomialFactorization) 有用SageMath写的。到 cocalc 试了下:

 

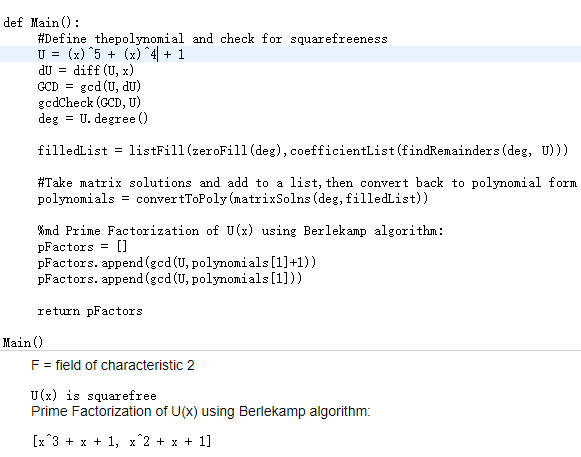
 结果不对。

SageMath is a free open-source mathematics software system. It builds on top of many existing packages: NumPy, SciPy, matplotlib, Sympy, Maxima, GAP, FLINT, R and many more. Access their combined power through a common, Python-based language or directly via interfaces or wrappers. SageMath-9.3-Installer-v0.6.3.exe 820.72 MB

SymPy is a Python library for symbolic mathematics. It aims to become a full-featured computer algebra system (CAS) while keeping the code as simple as possible in order to be comprehensible and easily extensible. SymPy is written entirely in Python. It uses mpmath, which is a free Python library for real and complex floating-point arithmetic with arbitrary precision.

Combinatorics is the branch of mathematics studying the enumeration, combination, and permutation of sets of elements and the mathematical relations that characterize their properties. Mathematicians sometimes use the term "combinatorics" to refer to a larger subset of discrete mathematics that includes graph theory. search(Combinatorics fourier)

六级/考研单词: mathematics, invert, exploit, implement, prime, log, manipulate, algebra, equate, seldom, thereby, insight, compute, finite, moderate, nowadays, digit, tertiary, symposium, hardware, parcel, intelligible, arithmetic, arbitrary, graph

 stackoverflow上有人说：把f(x)分解成因式就是找出f(x)=0的所有根。也许有些程序找到的不是1而是0.999999999。可x^4+1=0没有实数根啊。