3.7 枚举,记忆化

P4994 终于结束的起点 题解

一、题目分析

本题给定一个正整数 M（(2 <= M <= 706150)），任务是找出满足特定条件的最小正整数 n。这个条件是斐波那契数列的第 n 项 fib(n) 对 M 取模的结果为 0，并且第  (n + 1) 项 fib(n+1) 对 M 取模的结果为 1

已知斐波那契数列的定义如下：

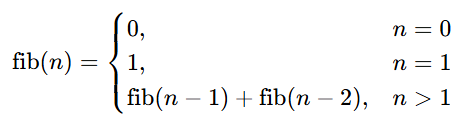
同时，题目中提到一个重要性质：对任意大于 1 的正整数 M 取模时，斐波那契数列会产生循环。这是因为 (fib(n−1)modM) 和 (fib(n−2)modM) 的组合最多只有 (M ^ 2) 种取值情况。随着数列项数的增加，在计算到 (M ^ 2) 次后，必然会出现重复的组合，从而进入循环状态。而且无论取什么模数 M，最终模 M 下的斐波那契数列都会呈现出 0,1,⋯,0,1,⋯ 的循环形式

二、解题思路

1. 暴力枚举思路：
   • 最直接的方法是从 (n = 1) 开始，按照斐波那契数列的定义依次计算每一项的值，然后对 M 取模，检查是否满足 fib(n)modM=0 且 fib(n+1)modM=1 的条件。如果不满足，则继续计算下一项，直到找到满足条件的 n
   • 但是这种方法存在严重的问题，因为直接递归计算斐波那契数列的时间复杂度是指数级的。例如，计算 fib(n) 时，会重复计算 fib(n−1) 和 fib(n−2) 中的很多项，导致计算量随着 n 的增大急剧增加，最终会超时（TLE），无法在规定时间内得到结果
2. 记忆化搜索优化思路：
   • 为了克服暴力枚举的效率问题，我们采用记忆化搜索的方法。具体来说，创建一个记忆数组 fp，用于存储已经计算过的斐波那契数列的项对 M 的取模结果
   • 在计算 fib(i) 时，首先检查 fp[i] 是否已经有值。如果 fp[i] 不为 0（表示已经计算过该项），则直接返回 fp[i]，避免重复计算。
   • 如果 fp[i] 为 0（表示尚未计算过该项），则按照斐波那契数列的定义进行计算，即 fib(i)=fib(i−1)+fib(i−2)，并将计算结果对 M 取模后存入 fp[i]，以便后续使用
   • 通过这种方式，每个位置的斐波那契数列项最多只需要计算一次，大大减少了计算量，将时间复杂度降低到线性级别，从而能够在规定时间内解决问题

三、代码实现

1. 暴力枚举代码：

#include <cstdio>
typedef long long ll;

// 递归计算斐波那契数列第n项
ll fib(ll n, ll m) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    return (fib(n - 1, m) + fib(n - 2, m)) % m;
}

int main() {
    ll m;
    scanf("%lld", &m);
    ll i = 1;
    // 循环检查，直到找到满足条件的i，即fib(i)对m取模为0且fib(i + 1)对m取模为1
    while (fib(i, m) != 0 || fib(i + 1, m) != 1) { 
        i++;
    }
    // 输出找到的满足条件的最小正整数i
    printf("%lld", i); 
    return 0;
}

2. 记忆化搜索优化代码：

#include<cstdio>
typedef long long ll;
using namespace std;
const ll INF = 0x7fffffff;
// 记忆数组，由于不确定n的具体大小，为了保证能存储所需数据，尽量开大，1千万的大小对于本题中M的取值范围基本足够
ll fp[10000002]; 
ll m;

// 计算斐波那契数列第i项对m取模的结果
ll f(ll i) {
    // 如果记忆数组中已经存储了该项的值，则直接返回
    if (fp[i]) return fp[i]; 
    // 当i为1或2时，根据斐波那契数列定义，值为1，对m取模后存入记忆数组并返回
    if (i == 1 || i == 2) return fp[i] = 1 % m; 
    // 当i大于2时，按照斐波那契数列定义计算当前项，并对m取模后存入记忆数组再返回
    else return fp[i] = (f(i - 1) + f(i - 2)) % m; 
}

int main() {
    // 读取输入的模数M
    scanf("%lld", &m); 
    ll i = 1; // 从1开始枚举n
    // 循环检查，直到找到满足条件的n，即f(i)对m取模为0且f(i + 1)对m取模为1
    while (f(i) != 0 || f(i + 1) != 1) { 
        i++;
    }
    // 输出找到的满足条件的最小正整数n
    printf("%lld", i); 
    return 0;
}