栈

概念

　　栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

　　栈是允许在同一端进行插入和删除操作的特殊线性表。允许进行插入和删除操作的一端称为栈顶(top)，另一端为栈底(bottom)；栈底固定，而栈顶浮动；栈中元素个数为零时称为空栈。插入一般称为进栈（PUSH），删除则称为退栈（POP）。栈也称为先进后出表。

　　栈可以用来在函数调用的时候存储断点，做递归时要用到栈！

用数组实现栈

class ArrayStack {

  private final int maxSize;
  private final int[] stack;
  private int top = -1;

  public ArrayStack(int maxSize){
    this.maxSize = maxSize;
    stack = new int[maxSize];
  }

  //栈是否满
  public boolean isFull(){
    return top == maxSize - 1;
  }

  //栈是否为空
  public boolean isEmpty(){
    return top == -1;
  }

  //入栈
  public void push(int value){
    if(isFull()){
      System.out.println("栈已满，不能添加数据");
      return;
    }
    top++;
    stack[top] = value;
  }

  //出栈
  public int pop(){
    if(isEmpty()){
      throw new RuntimeException("栈为空，没有数据");
    }
    int value = stack[top];
    top--;
    return value;
  }

  //从栈顶开始显示数据
  public void show(){
    if(isEmpty()){
      System.out.println("栈为空，没有数据");
    }
    for (int i = top; i >= 0; i--){
      System.out.printf("stack[%d]=%d\n",i,stack[i]);
    }
  }

}

测试

ArrayStack stack = new ArrayStack(3);
    Scanner scanner = new Scanner(System.in);
    boolean flag = true;
    String result;
    while (flag){
      System.out.println("show: 表示显示栈");
      System.out.println("exit: 退出程序");
      System.out.println("push: 表示添加数据到栈(入栈)");
      System.out.println("pop: 表示从栈取出数据(出栈)");
      System.out.println("请输入你的选择");
      result = scanner.next();
      switch (result) {
        case "show":
          stack.show();
          break;
        case "push":
          System.out.println("请输入一个数");
          int value = scanner.nextInt();
          stack.push(value);
          break;
        case "pop":
          try {
            int res = stack.pop();
            System.out.printf("出栈的数据是 %d\n", res);
          } catch (Exception e) {
            // TODO: handle exception
            System.out.println(e.getMessage());
          }
          break;
        case "exit":
          scanner.close();
          flag = false;
          break;
        default:
          break;
      }
    }
    System.out.println("程序退出~~~");

后进先出

用单向链表实现栈

class StackNode {
  public int value;
  public StackNode next;

  public StackNode(int value) {
    this.value = value;
  }

  @Override
  public String toString() {
    return "StackNode{" +
            "value=" + value +
            '}';
  }
}

class LinkedStack {

  private final StackNode head = new StackNode(0);

  //链表是否为空
  public boolean isEmpty(){
    return head.next == null;
  }

  //入栈
  public void push(int value){
    StackNode temp = head;
    while (temp.next != null){
      temp = temp.next;
    }
    temp.next = new StackNode(value);
  }

  //出栈
  public int pop(){
    if(isEmpty()){
      throw new RuntimeException("栈为空，没有数据");
    }
    StackNode temp = head;
    while (temp.next.next != null){
      temp = temp.next;
    }
    int value = temp.next.value;
    temp.next = null;
    return value;
  }

  //从栈顶开始显示数据
  public void show(){
    if(isEmpty()){
      System.out.println("栈为空，没有数据");
      return;
    }
    Stack<StackNode> stack = new Stack<>();
    StackNode temp = head.next;
    while (temp != null){
      stack.push(temp);
      temp = temp.next;
    }
    while (stack.size() > 0){
      System.out.println(stack.pop());
    }
  }

}

测试

 LinkedStack stack = new LinkedStack();
    Scanner scanner = new Scanner(System.in);
    boolean flag = true;
    String result;
    while (flag){
      System.out.println("show: 表示显示栈");
      System.out.println("exit: 退出程序");
      System.out.println("push: 表示添加数据到栈(入栈)");
      System.out.println("pop: 表示从栈取出数据(出栈)");
      System.out.println("请输入你的选择");
      result = scanner.next();
      switch (result) {
        case "show":
          stack.show();
          break;
        case "push":
          System.out.println("请输入一个数");
          int value = scanner.nextInt();
          stack.push(value);
          break;
        case "pop":
          try {
            int res = stack.pop();
            System.out.printf("出栈的数据是 %d\n", res);
          } catch (Exception e) {
            // TODO: handle exception
            System.out.println(e.getMessage());
          }
          break;
        case "exit":
          scanner.close();
          flag = false;
          break;
        default:
          break;
      }
    }
    System.out.println("程序退出~~~");

用栈实现计算器

只能计算单位数

class ArrayStack2 {

  private final int maxSize;
  private final int[] stack;
  private int top = -1;

  public ArrayStack2(int maxSize) {
    this.maxSize = maxSize;
    stack = new int[maxSize];
  }

  //获取栈顶的值
  public int peek() {
    return stack[top];
  }

  //栈是否满
  public boolean isFull(){
    return top == maxSize - 1;
  }

  //栈是否为空
  public boolean isEmpty(){
    return top == -1;
  }

  //入栈
  public void push(int value){
    if(isFull()){
      System.out.println("栈已满，不能添加数据");
      return;
    }
    top++;
    stack[top] = value;
  }

  //出栈
  public int pop(){
    if(isEmpty()){
      throw new RuntimeException("栈为空，没有数据");
    }
    int value = stack[top];
    top--;
    return value;
  }

  //从栈顶开始显示数据
  public void show(){
    if(isEmpty()){
      System.out.println("栈为空，没有数据");
    }
    for (int i = top; i >= 0; i--){
      System.out.printf("stack[%d]=%d\n",i,stack[i]);
    }
  }

  //判断是不是运算符
  public boolean isOperator(int val){
    return val == '+' || val == '-' || val == '*' || val == '/';
  }

  //返回运算符的优先级，数字越大，则优先级就越高.
  public int priority(int operator){
    if(operator == '*' || operator == '/'){
      return 1;
    }else if(operator == '+' || operator == '-'){
      return 0;
    }else {
      return -1;
    }
  }

  //计算
  public int cal(int num1, int num2, int operator) {
    int result = 0;
    switch (operator){
      case '+':
        result = num1 + num2;
        break;
      case '-':
        result = num2 - num1;// 注意顺序
        break;
      case '*':
        result = num1 * num2;
        break;
      case '/':
        result = num2 / num1;
        break;
      default:
        break;
    }
    return result;
  }

}

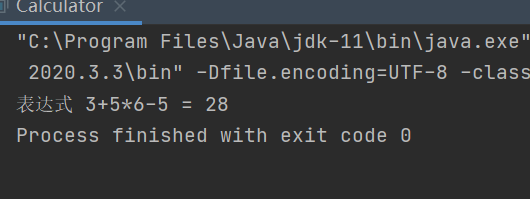
 String expression = "3+5*6-5";
    //存放数字的栈
    ArrayStack2 numStack = new ArrayStack2(10);
    //存放运算符的栈
    ArrayStack2 operatorStack = new ArrayStack2(10);
    int num1;
    int num2;
    int result;
    char ch ;
    int index = 0;
    int operator;
    do {
      ch = expression.substring(index, index + 1).charAt(0);
      //判断是不是运算符
      if (operatorStack.isOperator(ch)) {
        //如果存放运算符的栈是空的，直接将运算符放进去
        if (!operatorStack.isEmpty()) {
          //如果运算符的优先级小于等于栈顶的优先级，就弹出数栈的两个值，符栈的一个值进行运算
          //将得到的值放入数栈中，运算符放入符栈
          if (operatorStack.priority(ch) <= operatorStack.priority(operatorStack.peek())) {
            num1 = numStack.pop();
            num2 = numStack.pop();
            operator = operatorStack.pop();
            result = numStack.cal(num1, num2, operator);
            numStack.push(result);
          }
        }
        operatorStack.push(ch);
      } else {
　　　　　//ch现在是字符，对应的埃斯格玛与数字差了48
        numStack.push(ch - 48);

      }
      index++;
    } while (index != expression.length());

    while (!operatorStack.isEmpty()) {
      num1 = numStack.pop();
      num2 = numStack.pop();
      operator = operatorStack.pop();
      result = numStack.cal(num1, num2, operator);
      numStack.push(result);
    }

    int result2 = numStack.pop();
    System.out.printf("表达式 %s = %d", expression, result2);

计算多位数

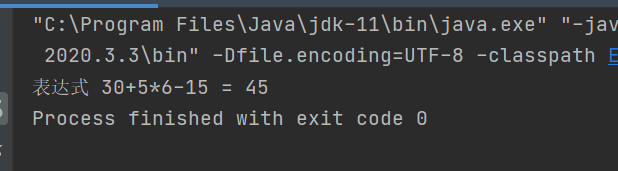
　　使用一个变量来存储是数字的值，如果下一个值是运算符就将这个变量存入数栈中，并清空它的值

 String expression = "30+5*6-15";
    //存放数字的栈
    ArrayStack2 numStack = new ArrayStack2(10);
    //存放运算符的栈
    ArrayStack2 operatorStack = new ArrayStack2(10);
    int num1;
    int num2;
    int result;
    char ch ;
    int index = 0;
    int operator;
    String res = "";
    do {
      ch = expression.substring(index, index + 1).charAt(0);
      //判断是不是运算符
      if (operatorStack.isOperator(ch)) {
        //如果存放运算符的栈是空的，直接将运算符放进去
        if (!operatorStack.isEmpty()) {
          //如果运算符的优先级小于等于栈顶的优先级，就弹出数栈的两个值，符栈的一个值进行运算
          //将得到的值放入数栈中，运算符放入符栈
          if (operatorStack.priority(ch) <= operatorStack.priority(operatorStack.peek())) {
            num1 = numStack.pop();
            num2 = numStack.pop();
            operator = operatorStack.pop();
            result = numStack.cal(num1, num2, operator);
            numStack.push(result);
          }
        }
        operatorStack.push(ch);
      } else {
//        numStack.push(ch - 48);
        res += ch;
        if(index == expression.length()-1){
          numStack.push(Integer.parseInt(res));
        } else {
          //如果下一个是运算符，就将res的值放入数栈中，并将res清空
          if(operatorStack.isOperator(expression.substring(index + 1,index + 2).charAt(0))) {
            numStack.push(Integer.parseInt(res));
            res = "";
          }
        }
      }
      index++;
    } while (index != expression.length());

    while (!operatorStack.isEmpty()) {
      num1 = numStack.pop();
      num2 = numStack.pop();
      operator = operatorStack.pop();
      result = numStack.cal(num1, num2, operator);
      numStack.push(result);
    }

    int result2 = numStack.pop();
    System.out.printf("表达式 %s = %d", expression, result2);

前缀表达式

　　前缀表达式是一种没有括号的算术表达式，与中缀表达式不同的是，其将运算符写在前面，操作数写在后面。为纪念其发明者波兰数学家Jan Lukasiewicz，前缀表达式也称为“波兰式”。例如，- 1 + 2 3，它等价于1-(2+3)。

　　后缀表达式源自于前缀表达式，为了区分前缀和后缀表示，通常将后缀表示称为逆波兰表示；因前缀表示并不常用，所以有时也将后缀表示称为波兰表示。

　　前缀表达式是一种十分有用的表达式，将中缀表达式转换为前缀表达式后，就可以只依靠出栈、入栈两种简单操作完全解决中缀表达式的全部运算。

中缀表达式

　　（或中缀记法）是一个通用的算术或逻辑公式表示方法，操作符是以中缀形式处于操作数的中间（例：3 + 4），中缀表达式是人们常用的算术表示方法。

　　与前缀或后缀记法不同的是，中缀记法中括号是必需的。计算过程中必须用括号将操作符和对应的操作数括起来，用于指示运算的次序。

后缀表达式

　　逆波兰式（Reverse Polish notation，RPN，或逆波兰记法），也叫后缀表达式（将运算符写在操作数之后）

作用

　　实现逆波兰式的算法，难度并不大，但为什么要将看似简单的中缀表达式转换为复杂的逆波兰式？原因就在于这个简单是相对人类的思维结构来说的，对计算机而言中序表达式是非常复杂的结构。相对的，逆波兰式在计算机看来却是比较简单易懂的结构。因为计算机普遍采用的内存结构是栈式结构，它执行先进后出的顺序。

算法实现

　　首先需要分配2个栈，一个作为临时存储运算符的栈S1（含一个结束符号），一个作为存放结果（逆波兰式）的栈S2（空栈）从中缀式的左端开始取字符，逐序进行如下步骤：

若取出的字符是操作数，则分析出完整的运算数，该操作数直接送入S2栈。
若取出的字符是运算符，则将该运算符与S1栈栈顶元素比较，如果该运算符(不包括括号运算符)优先级高于S1栈栈顶运算符（包括左括号）优先级，则将该运算符进S1栈，否则，将S1栈的栈顶运算符弹出，送入S2栈中，直至S1栈栈顶运算符（包括左括号）低于（不包括等于）该运算符优先级时停止弹出运算符，最后将该运算符送入S1栈。
若取出的字符是“（”，则直接送入S1栈顶。
若取出的字符是“）”，则将距离S1栈栈顶最近的“（”之间的运算符，逐个出栈，依次送入S2栈，最后弹出“（”。
重复上面的1~4步，直至处理完所有的输入字符。

　S2应做一下逆序处理。便可以按照逆波兰式的计算方法计算了！

逆波兰计算器

 //将表达式存入集合中
  public static List<String> getListString(String suffixExpression) {
    String[] split = suffixExpression.split(" ");
    List<String> list = new ArrayList<>();
    Collections.addAll(list, split);
    return list;
  }

  //计算
  public static int calculate(List<String> ls) {
    Stack<String> stack = new Stack<>();
    for (String item : ls){
      if (item.matches("\\d+")) { // 匹配的是多位数
        // 入栈
        stack.push(item);
      } else {
        int num1 = Integer.parseInt(stack.pop());
        int num2 = Integer.parseInt(stack.pop());
        int result;
        switch (item) {
          case "+":
            result = num1 + num2;
            break;
          case "-":
            result = num2 - num1;
            break;
          case "*":
            result = num1 * num2;
            break;
          case "/":
            result = num1 / num2;
            break;
          default:
            throw new RuntimeException("运算符有误");
        }
        //把result 入栈
        stack.push("" + result);
      }
    }
    return Integer.parseInt(stack.pop());
  }

 　　 String suffixExpression = "30 4 + 5 * 6 -";
    List<String> list = getListString(suffixExpression);
    System.out.println("list = " + list);
    int result = calculate(list);
    System.out.println("result = " + result);

中缀表达式转后缀表达式

//将中缀表达式存入到集合中
  public static List<String> toInfixExpressionList(String s) {
    List<String> list = new ArrayList<>();
    int i = 0;
    char ch;
    StringBuilder str;
    do{
      //判断是不是运算符
      if((ch = s.charAt(i)) < 48 || (ch = s.charAt(i))  > 57){
        list.add("" + ch);
        i++;
      } else {
        str = new StringBuilder();
        //如果是数字，存入str中，下一位是运算符就结束循环，将str存入集合中
        while (i < s.length() && s.charAt(i) >= 48 && (ch = s.charAt(i))  <= 57){
          str.append(ch);
          i++;
        }
        list.add(str.toString());
      }
    }while (i < s.length());
    return list;
  }

  //中缀表达式转后缀表达式，由于s2并不需要弹出数据,最后还需要逆序处理，直接用集合代替
  public static List<String> parseSuffixExpressionList(List<String> ls) {
    Stack<String> s1 = new Stack<>();
    List<String> s2 = new ArrayList<>();
    for (String item : ls) {
      if(item.matches("\\d+")) {
        s2.add(item);
      } else if (item.equals("(")) {
        s1.push(item);
      } else if (item.equals(")")) {
        while (!s1.peek().equals("(")) {
          s2.add(s1.pop());
        }
        s1.pop();
      } else {
        while (s1.size() > 0 && Operation.getValue(item) <= Operation.getValue(s1.peek())) {
          s2.add(s1.pop());
        }
        s1.push(item);
      }
    }
    while (s1.size() > 0){
      s2.add(s1.pop());
    }
    return s2;
  }

class Operation {

  //写一个方法，返回对应的优先级数字
  public static int getValue(String operation) {
    int result = 0;
    switch (operation) {
      case "+":
      case "-":
        result = 1;
        break;
      case "*":
      case "/":
        result = 2;
        break;
      default:
        System.out.println("不存在该运算符" + operation);
        break;
    }
    return result;
  }

}

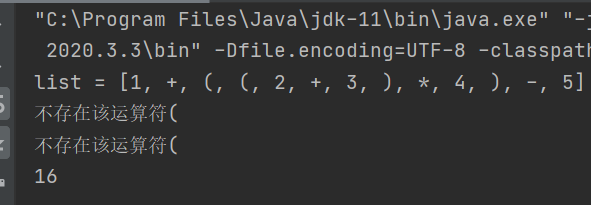
　　 String expression = "1+((2+3)*4)-5";
    List<String> list = toInfixExpressionList(expression);
    System.out.println("list = " + list);
    List<String> suffixExpressionList = parseSuffixExpressionList(list);
    System.out.println(calculate(suffixExpressionList));

完整逆波兰计算器

 /**
   * 匹配 + - * / ( ) 运算符
   */
  static final String SYMBOL = "[+\\-*/()]";

  static final String LEFT = "(";
  static final String RIGHT = ")";
  static final String ADD = "+";
  static final String MINUS= "-";
  static final String TIMES = "*";
  static final String DIVISION = "/";

  /**
   * 加減 + -
   */
  static final int LEVEL_01 = 1;
  /**
   * 乘除 * /
   */
  static final int LEVEL_02 = 2;

  /**
   * 括号优先级最高
   */
  static final int LEVEL_HIGH = Integer.MAX_VALUE;


  static Stack<String> stack = new Stack<>();
  static List<String> data = Collections.synchronizedList(new ArrayList<>());

  /**
   * 去除所有空白符
   */
  public static String replaceAllBlank(String s ){
    // \\s+ 匹配任何空白字符，包括空格、制表符、换页符等等, 等价于[ \f\n\r\t\v]
    return s.replaceAll("\\s+","");
  }

  /**
   * 判断是不是数字 int double long float
   */
  public static boolean isNumber(String s){
    Pattern pattern = Pattern.compile("^[-+]?[.\\d]*$");
    return pattern.matcher(s).matches();
  }

  /**
   * 判断是不是运算符
   */
  public static boolean isSymbol(String s){
    return s.matches(SYMBOL);
  }

  /**
   * 匹配运算等级
   */
  public static int calcLevel(String s){
    if("+".equals(s) || "-".equals(s)){
      return LEVEL_01;
    } else if("*".equals(s) || "/".equals(s)){
      return LEVEL_02;
    }
    return LEVEL_HIGH;
  }

  /**
   * 匹配
   */
  public static List<String> doMatch (String s) {
    if(s == null || "".equals(s.trim())) throw new RuntimeException("data is empty");
    if(!isNumber(s.charAt(0)+"")) throw new RuntimeException("data illegal,start not with a number");

    s = replaceAllBlank(s);

    String each;
    int start = 0;

    for (int i = 0; i < s.length(); i++) {
      if(isSymbol(s.charAt(i)+"")){
        each = s.charAt(i)+"";
        //栈为空，(操作符，或者 操作符优先级大于栈顶优先级 && 操作符优先级不是( )的优先级 及是 ) 不能直接入栈
        if(stack.isEmpty() || LEFT.equals(each)
                || ((calcLevel(each) > calcLevel(stack.peek())) && calcLevel(each) < LEVEL_HIGH)){
          stack.push(each);
        }else if( !stack.isEmpty() && calcLevel(each) <= calcLevel(stack.peek())){
          //栈非空，操作符优先级小于等于栈顶优先级时出栈入列，直到栈为空，或者遇到了(，最后操作符入栈
          while (!stack.isEmpty() && calcLevel(each) <= calcLevel(stack.peek()) ){
            if(calcLevel(stack.peek()) == LEVEL_HIGH){
              break;
            }
            data.add(stack.pop());
          }
          stack.push(each);
        }else if(RIGHT.equals(each)){
          // ) 操作符，依次出栈入列直到空栈或者遇到了第一个)操作符，此时)出栈
          while (!stack.isEmpty()){
            calcLevel(stack.peek());
            if(LEVEL_HIGH == calcLevel(stack.peek())){
              stack.pop();
              break;
            }
            data.add(stack.pop());
          }
        }
        start = i ;    //前一个运算符的位置
      }else if( i == s.length()-1 || isSymbol(s.charAt(i+1)+"") ){
        each = start == 0 ? s.substring(start,i+1) : s.substring(start+1,i+1);
        if(isNumber(each)) {
          data.add(each);
          continue;
        }
        throw new RuntimeException("data not match number");
      }
    }
    //如果栈里还有元素，此时元素需要依次出栈入列，可以想象栈里剩下栈顶为/，栈底为+，应该依次出栈入列，可以直接翻转整个stack 添加到队列
    Collections.reverse(stack);
    data.addAll(new ArrayList<>(stack));

    System.out.println(data);
    return data;
  }

  /**
   * 算出结果
   */
  public static Double doCalc(List<String> list){
    double d;
    if(list == null || list.isEmpty()){
      return null;
    }
    if (list.size() == 1){
      d = Double.parseDouble(list.get(0));
      return d;
    }
    ArrayList<String> list1 = new ArrayList<>();
    for (int i = 0; i < list.size(); i++) {
      list1.add(list.get(i));
      if(isSymbol(list.get(i))){
        Double d1 = doTheMath(list.get(i - 2), list.get(i - 1), list.get(i));
        list1.remove(i);
        list1.remove(i-1);
        list1.set(i-2,d1+"");
        list1.addAll(list.subList(i+1,list.size()));
        break;
      }
    }
    return doCalc(list1);
  }

  /**
   * 运算
   */
  public static Double doTheMath(String s1,String s2,String symbol){
    Double result ;
    switch (symbol){
      case ADD : result = Double.parseDouble(s1) + Double.parseDouble(s2); break;
      case MINUS : result = Double.parseDouble(s1) - Double.parseDouble(s2); break;
      case TIMES : result = Double.parseDouble(s1) * Double.parseDouble(s2); break;
      case DIVISION : result = Double.parseDouble(s1) / Double.parseDouble(s2); break;
      default : result = null;
    }
    return result;

  }

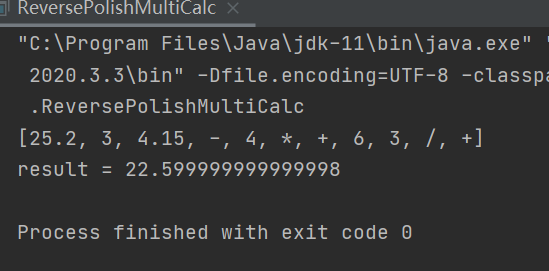
 String math = "25.2 + (3 - 4.15)*4+6/3";
    try {
      double result = doCalc(doMatch(math));
      System.out.println("result = " + result);
    } catch (Exception e) {
      e.printStackTrace();
    }

posted @ 2021-08-04 19:17 翻蹄亮掌一皮鞋阅读(261) 评论(0) 收藏举报

刷新页面返回顶部

偷得浮生半日闲

栈

概念