基本排序算法实现

一、简单选择排序

　　1、简单选择排序的思想是这样的：首先，找到数组中最小的元素，其次，将它和数组中的第一个元素交换位置。再次，在剩下的元素中寻找最小的元素，然后将它和数组中第二个元素交换位置，这样往复进行，知道到数组中最后一个元素的时候就变成了有序数组。

　　2、简单选择排序算法：对于长度为N的数组，需要N² /2次比较和N次交换。

　　3、下面是一次选择排序的流程：从下面的流程中我们可以看出，对于长度为N的数组，需要的比较次数为(N-1)+(N-2)+......+1~N² /2

　

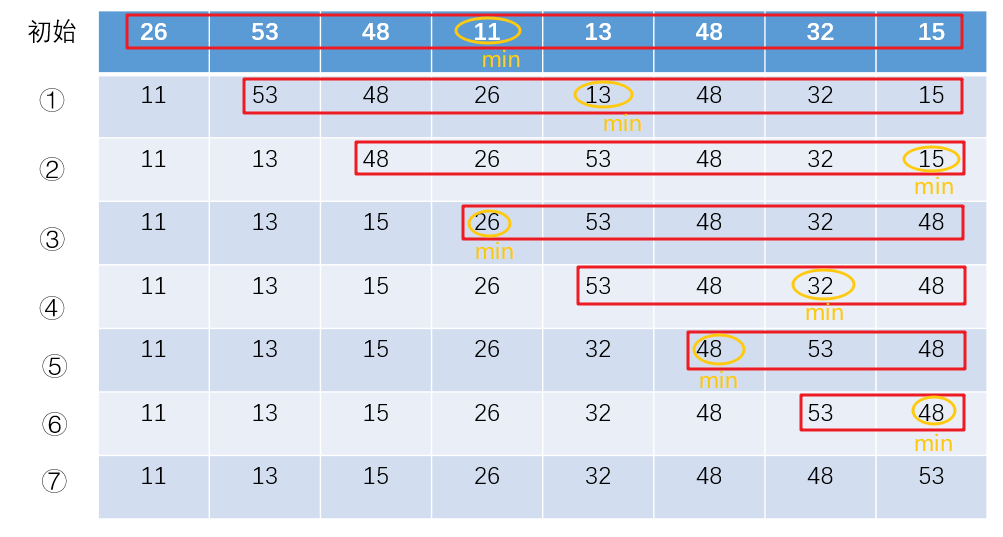
　　3、简单选择排序的特点：①运行时间和输入无关，不管初始状态如何，为了找出当前最小的元素总是需要遍历当前数组。②数据移动是最少的，主要体现在这种排序只需要交换N次数据。

　　4、下面是简单选择排序的Java代码实现，并得到和上面手动按照选择排序流程得到的结果一样

package cn.select;

public class SelectSort {

    private static int[] testArray = {26, 53, 48, 11, 13, 48, 32, 15};
    
    public static void main(String[] args) {
        selectSort();
        for (int i = 0; i < testArray.length; i++) {
            System.out.println(testArray[i]);
        }
    }
    
    public static void selectSort() {
        for (int i = 0; i < testArray.length; i++) {
            int min = i; //当前最小元素的索引
            //遍历剩余的数组
            for (int j = i + 1; j < testArray.length; j++) {
                //比较当前数和最小数组元素索引值
                if(testArray[j] < testArray[min]) {
                    min = j;
                }
            }
            int temp = testArray[i];
            testArray[i] = testArray[min];
            testArray[min] = temp;
        }
    }
    
}

二、插入排序

　　1、在普通的插入排序中，为了给出插入腾出空间，我们需要将后续的元素都向后移动一位（相比当前插入的位置）。

　　2、下面是一个插入排序的流程

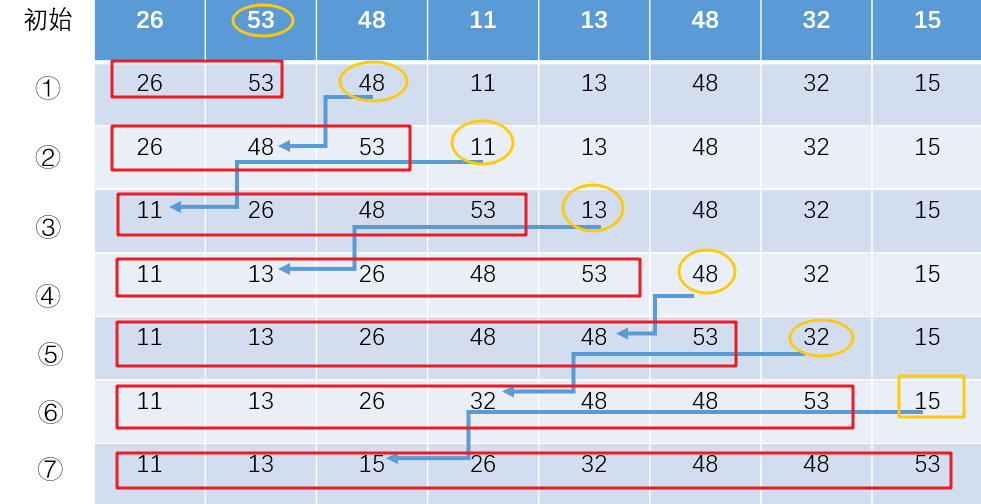
　　3、下面是插入排序的代码实现，运行的结果和上面手动执行的结果是一样的

package cn.insert;

public class InsertSort {

    private static int[] testArray = {26, 53, 48, 11, 13, 48, 32, 15};
    
    public static void main(String[] args) {
        insertSort();
        for (int i = 0; i < testArray.length; i++) {
            System.out.print(testArray[i] + " ");
        }
    }
    
    public static void insertSort() {
        for (int i = 1; i < testArray.length; i++) {
            //得到遍历时候当前索引下面的值，然后和前面排序号的数组元素进行比较，插入到合适的位置
            for (int j = i; j > 0 && less(testArray[j], testArray[j-1]); j--) {
                int temp = testArray[j];
                testArray[j] = testArray[j - 1];
                testArray[j - 1] = temp;
            }
        }
    }
    
    public static boolean less(int a, int b) {
        if(a < b) return true;
        return false;
    }
    
}

　　4、另外在说明一点简单插入排序和简单选择排序的不同点，在给定数组部分有序的情况下，插入排序的执行次数是小于选择排序的（选择排序无论是在有序还是无序的情况下都是一样的执行次数）

三、希尔排序

　　1、希尔排序是一种基于插入排序的算法。插入对于大规模乱序的数组，只会交换相邻的元素（元素只能从一端慢慢的移动到另一端）。希尔排序采用不相邻元素交换以及对数组局部进行排序的方式并最终使用插入排序再将局部数有序数组进行排序；

　　2、希尔排序的思想是：任何相隔为h的两个元素都是有序的（对应上面的不相邻元素交换，使得两个元素有序），这样的数组也被称为h有序数组。在实际的排序中，一般会将h从打到小变化，这样首先是将大的数据移动到整个数组的右边，从而为更小的h有序数组排序制造方便。下面的例子中使用的是N/3的方式计算和更新h的值。

　　3、实现希尔排序的方式：在每一个h数组中，将大的元素移动到后面，我们只需要将插入排序的代码中的相邻元素更改为相隔h的元素比较并交换。这样，希尔排序就改成了使用插入排序但是不同增量（由1变为h）的过程。

　　4、下面是手动采用希尔排序的特点实现的一个排序

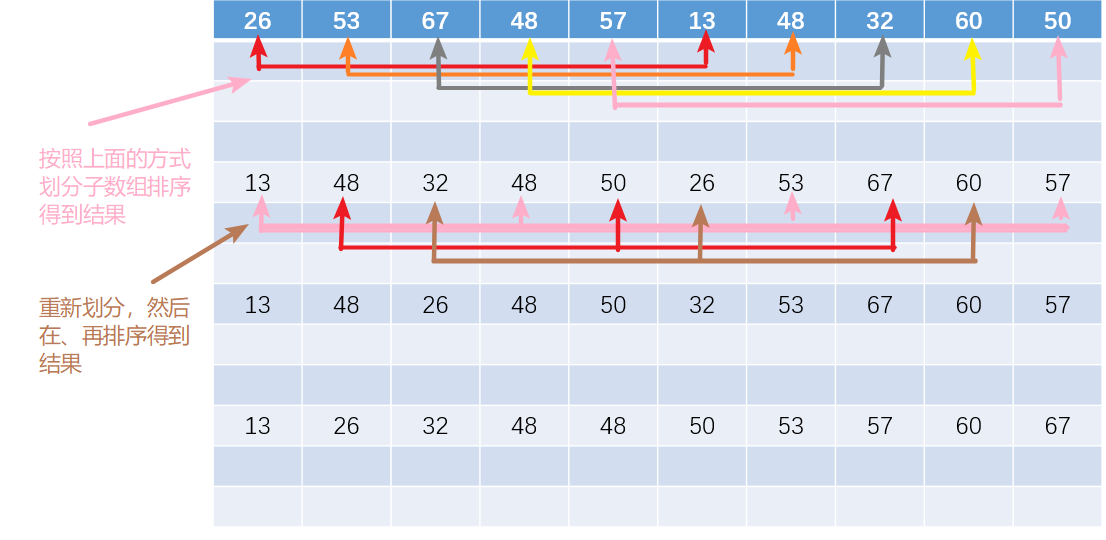
　　5、这是希尔排序的代码，运行的结果和手动计算的结果是一样的

package cn.shell;

public class ShellSort {

    private static int[] array = {26, 53, 48, 11, 13, 48, 32, 15, 34, 45, 56, 78, 4};
    
    public static void main(String[] args) {
        shellSort();
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
    }
    
    private static void shellSort() {
        int h = 1;
        //计算h的最大值
        while(h < array.length/3) {
            //比如当前的array长度为13，那么h最大值就是4
            //那么h的取值就是1 ，4，按照长度为这三种情况的子数组进行排序
            h = 3 * h + 1;
        }
        while(h >= 1) {
            for (int i = h; i < array.length; i++) {
                //比较当前子数组中值，基于当前子数组进行排序
                for (int j = i; j >= h && less(array[j], array[j - h]); j -= h) {
                    int temp = array[j];
                    array[j] = array[j - h];
                    array[j - h] = temp;
                }
            }
            //每次计算玩，进行下一轮排序的时候更新h的值
            h = h / 3;
        }
        
    }
    public static boolean less(int a, int b) {
        if(a < b) return true;
        return false;
    }
}

四、快速排序

　　1、快速排序是一种基于分治的算法，将一个数组分成两个数组，然后将两部分独立排序。下面是快速排序的一个递归实现（其中没有添加上查找切分位置的模块）

public static void quickSort(int p, int r) {
        if(p < r) {
            int q = partition(p, r);
            quickSort(p, q - 1);
            quickSort(q + 1, r);
        }
    }

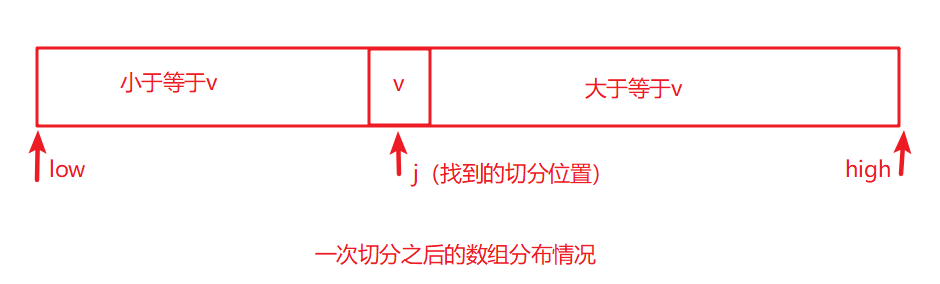
　　2、在介绍切分方法之前，我们先说明一下切分之后整个数组需要满足的条件（假设现在切分位置为 j ）：

　　①array[0] 到array[j-1] 中的元素都不大于a[j];

　　②array[j+1]到array[len-1]的元素都不小于a[j];

　　我们可以用下面这个图来直观显示一下一次切分后整个数组的情况（我们会在下面描述一般情况下切分的思想，以及代码实现）

　　

　　2、在上面的代码中，我们可以看到，在递归实现快排之前，我们需要找到切分元素的位置。那么如何找到切分元素的位置呢？可以这样描述一下切分过程：

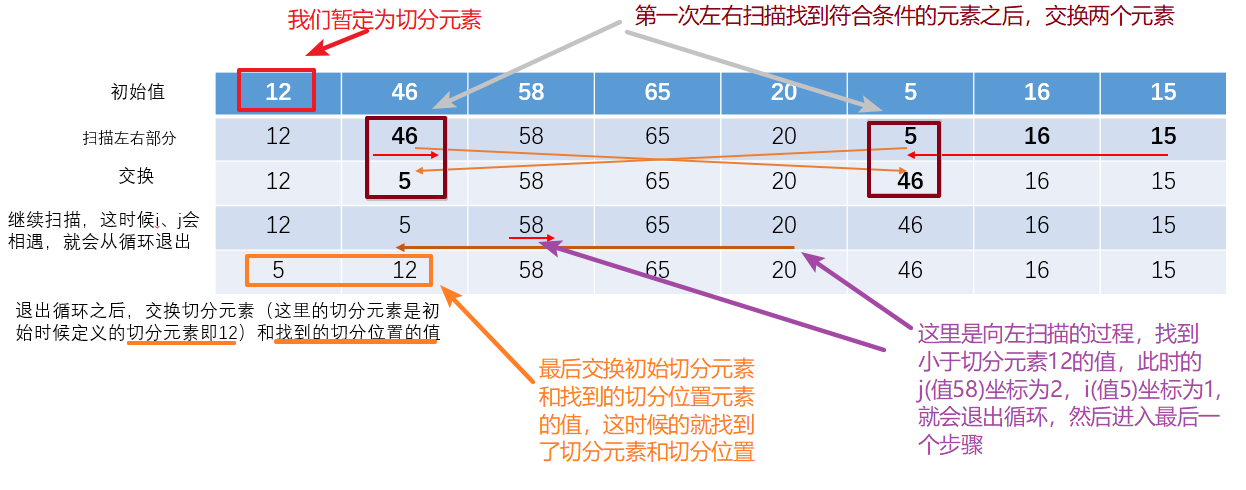
　　一般情况下，我们可以首先先选择array[0]作为切分元素，然后我们从数组的左端（记作i）开始向右遍历扫描知道找到一个大于等于它的元素，再从数组右边（记作j）开始向左扫描知道找到一个小于等于它的元素。这两个元素相对于我们选定的位置而言是没有排序的，所以我们需要交换他们的位置。按照这样的方式进行循环，我们就能保证遍历之后，i的左侧都小于i所在的位置的元素值，j右侧元素都小于j所在位置的元素值。最后，当i和j相等的时候，表示查找完毕，这时候，我们就将开始选择的切分元素array[0]和array[j]两个位置的元素交换即可，这时候j所在的位置就是上面图中的切分位置。

　　3、下面是个简单的过程图（切分之前，和切分过程中(i和j没有相遇之前)，切分完成之后的图和上面的图一样）

　　

　　4、下面是一个未排序的初始数组经过一次切分之后的过程图，假设数组为{12,46,58,65,20,5,16,15}，参考下面的额图解理解一次切分的整个过程

　　

　　5、在给出Java实现的简单测试代码，运行结果为

package cn.quick;

public class QuickSort {
    
    public static void main(String[] args) {
        int[] testArray = {12,46,58,65,20,5,16,15};
        quickSort(testArray, 0, testArray.length-1);
        for (int i = 0; i < testArray.length; i++) {
            System.out.print(testArray[i] + " ");
        }
    }
    
    public static int partition(int[] testArray, int low, int high) {
        int i = low, j = high + 1;
        int var = testArray[low];
        while(true) {
            //从数组的左端（记作i）开始向右遍历扫描知道找到一个大于等于它的元素
            while(less(testArray[++i], var)) {
                if(i == high) break;
            }
            //从数组右边（记作j）开始向左扫描知道找到一个小于等于它的元素
            while(less(var, testArray[--j])) {
                if(j == low) break;
            }
            if(i >= j) break;
            //这是最后i和j相遇之后，交换i和j所在位置元素的值
            int temp = testArray[j];
            testArray[j] = testArray[i];
            testArray[i] = temp;
        }
        int t = testArray[low];
        testArray[low] = testArray[j];
        testArray[j] = t;
        
        return j;
    }
    
    public static void quickSort(int[] testArray,int p, int r) {
        if(p < r) {
            int q = partition(testArray, p, r);
            quickSort(testArray, p, q - 1);
            quickSort(testArray, q + 1, r);
        }
    }
    
    public static boolean less(int a, int b) {
        if(a <= b) return true;
        return false;
    }
}