A. Stable Arrangement of Rooks

A. Stable Arrangement of Rooks

time limit per test:1 second

memory limit per test:256 megabytes

input:standard input

output:standard output

You have an n×nn×n chessboard and kk rooks. Rows of this chessboard are numbered by integers from 11 to nn from top to bottom and columns of this chessboard are numbered by integers from 11 to nn from left to right. The cell (x,y)(x,y) is the cell on the intersection of row xx and collumn yy for 1≤x≤n1≤x≤n and 1≤y≤n1≤y≤n.

The arrangement of rooks on this board is called good, if no rook is beaten by another rook.

A rook beats all the rooks that shares the same row or collumn with it.

The good arrangement of rooks on this board is called not stable, if it is possible to move one rook to the adjacent cell so arrangement becomes not good. Otherwise, the good arrangement is stable. Here, adjacent cells are the cells that share a side.

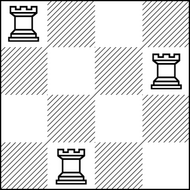Such arrangement of 33 rooks on the 4×44×4 chessboard is good, but it is not stable: the rook from (1,1)(1,1) can be moved to the adjacent cell (2,1)(2,1) and rooks on cells (2,1)(2,1) and (2,4)(2,4) will beat each other.

Please, find any stable arrangement of kk rooks on the n×nn×n chessboard or report that there is no such arrangement.

Input

The first line contains a single integer tt (1≤t≤1001≤t≤100) — the number of test cases.

The first line of each test case contains two integers nn, kk (1≤k≤n≤401≤k≤n≤40) — the size of the chessboard and the number of rooks.

Output

If there is a stable arrangement of kk rooks on the n×nn×n chessboard, output nn lines of symbols . and R. The jj-th symbol of the ii-th line should be equals R if and only if there is a rook on the cell (i,j)(i,j) in your arrangement.

If there are multiple solutions, you may output any of them.

If there is no stable arrangement, output −1−1.

Example

input

5
3 2
3 3
1 1
5 2
40 33

output

..R
...
R..
-1
R
.....
R....
.....
....R
.....
-1

Note

In the first test case, you should find stable arrangement of 22 rooks on the 3×33×3 chessboard. Placing them in cells (3,1)(3,1) and (1,3)(1,3) gives stable arrangement.

In the second test case it can be shown that it is impossbile to place 33 rooks on the 3×33×3 chessboard to get stable arrangement.

思路：本题要你求的是一个稳定排序，如果有多个解决方案只需要输出一个就够，如果没有就输出-1。这道题的想法是，当棋子的数量k小于行列数的(n+1)/2向下取整时一定有解的（这个式子你可以理解为两个棋子中间空一行+一列）。而且这个解我们默认放在主对角线上，两个棋子的坐标为x==y，坐标点间隔都相差2，输出R，其余都是.。

题解：

#include <iostream> //有点类似leetcode用函数求解，0.0
using namespace std;
void chess(int cheBor, int rooks) {
    int maxChe = (cheBor +1)/2;
    if (maxChe < rooks) {
        int ou = -1;
        cout << ou << endl;
    }
    else {
        int flag = -2;
        for (int i = 0; i < cheBor; i++) {
            for (int j = 0; j < cheBor; j++) {
                if (i == j && (i - flag) == 2) {
                    if (rooks > 0) {
                        cout << 'R';
                        flag = i;
                        rooks--;
                    } else
                        cout << '.';
                } else {
                    cout << '.';
                }
            }
            cout << endl;
        }
    }
}
int main() {
    int num = 0;
    cin >> num;
    int arr[num][2];
    for (int i = 0; i < num; ++i) {
        cin >> arr[i][0] >> arr[i][1];
    }
    for (int j = 0; j < num; ++j) {
        chess(arr[j][0],arr[j][1]);
    }
    return 0;
}