拉格朗日乘子法、对偶问题、KKT条件、半二次方分裂法、ADMM

To Be Continued~

共轭函数

假设 \(f: \mathbb{R}^n \rightarrow \mathbb{R}\)，函数 \(f^*: \mathbb{R} \rightarrow \mathbb{R}\)。若两函数满足：

\[f^*(y) = \underset{x \in dom f}{\sup} (y^Tx-f(x)) \]

则 \(f^*\) 是 \(f\) 的共轭函数，共轭函数是使上式的上确界小于 \(\infty\) 的部分。可以理解为对于每一个确定的 \(y\)，\(y^Tx\) 都是一个线性函数，此时 \(y^Tx - f(x)\) 变为线性函数与原函数在 \(x\) 的定义域上的差值，这个差值即为 \(y^Tx - f(x)\) 的值域，若此时确定的 \(y\) 不能使值域的上确界小于无穷大，则不保留，反之则保留。所有保留的 \(y\) 构成共轭函数的定义域，而所有 \(y^Tx - f(x)\) 不是 \(\infty\) 的上确界构成共轭函数的值域。
易知共轭函数是凸函数

示例

• 放射函数：\(f(x) = ax +b\) 的共轭函数为：

\[f^*(y) = \sup (yx - ax -b) \]

观察易得，如果 \(y \ne a\) ，那么无论 \(y\) 取值多少，\(yx - ax -b\) 的上确界都是 \(\infty\)。但是当 \(y = a\) 时，\(yx - ax -b\) 为常数 \(-b\)，上确界为 \(-b\)，即此共轭函数定义域为 \(a\)，值域为 \(-b\)。

• 负对数函数：\(f(x) = -\log x\)的共轭函数为：

\[f^*(y) = \underset{x \gt 0}{\sup} (yx + \log x) \]

首先\(f^*(y)^{\prime\prime} \lt 0，\) 对于某一 \(y\) 有 \(f^*(y)^{\prime} = y + \frac{1}{x} = 0\) 时，共轭函数取得最大值，此时 \(x = -\frac{1}{y}\) 使得共轭函数取得上确界，即共轭函数简化为 \(f^*(y) = -\log(-y) - 1\)

拉格朗日乘子法

首先解释拉格朗日函数的形式的原因

由简单的二维形式，并且受到等式约束的例子出发

\[\begin{aligned} &\min f(x,y) \\ &s.t. \quad g(x,y) = c \end{aligned} \]

其中 \(g(x,y) = c\) 可以理解为等高线，即 \(z = g(x,y)\) 为三维曲面，当 \(z = c\) 时，可以想象为用平面 \(z = c\) 去截 \(z = g(x,y)\) 这个三维曲面所获得的曲线，而这条曲线上满足
\(g(x,y) = c\)。同理，如图蓝色线所示为三维曲面 \(f(x,y)\) 的各个等高线。如果没有约束，很显然最值会落到最小的圈里面。正是有了约束，\(x,y\) 需要同时在蓝色和绿色线上，那么最值点就应该是两条等高线相切的时候取得，因为如果仅仅是相交，就还在内部或者外部存在其他等高线使得取得的值更大或者更小，只有相切的时候，可能取得最优值。

很显然想要两者相切必然有 \(f(x,y)\) 与 \(g(x,y)=C\) 的梯度一定是平行，则有 \(\nabla f(x,y) = \lambda (g(x,y)-C)\)。所以就容易理解当拉格朗日函数 \(F(x,y) = f(x,y) + \lambda (g(x,y) -C)\) 取得极值时就等价于两者的梯度平行。特别地，当拉格朗日函数所有点满足等式约束 \(g(x,y)=C\) 时两个函数完全等价的。因此 \(F(x,y)\) 最优若等价于 \(f(x,y)\) 最优需要满足：

\[\begin{cases} F_x^{\prime} = 0 \\ F_y^{\prime} = 0 \\ g(x,y) = C \ \& \ \lambda \ne 0 \end{cases} \]

事实上，这种做法等价于利用等式约束来进行换元后，变为无约束的情况，从而按照一般的求最值来求得最优解。

那么给出带约束的原问题的一般形式：

\[\begin{cases} &\min f(x,y) \\ &s.t. \quad m_i(x) = 0 \ (i=1,2,...,m), n_j(x) \le 0 \ (j=1,2,...,n) \end{cases} \]

即既有等式约束又有不等式约束（不等式约束，可以将其想象为一个范围，而这个范围依然是有边界的，边界就是等式约束，取得最优点一般会在边界处），这样可以得到拉格朗日函数

\[L(x,\lambda,\nu)=f(x)+\sum_{i=1}^m \lambda_i m_i(x) + \sum_{j=1}^n \nu_j n_j(x) \]

其中 $\nu_j \ge 0 $

同理，若我们想要 \(L(x,\lambda,\nu)\) 与 \(f(x)\) 同时取得最优，需要满足等式约束，而不等式约束到达边界（即取到等号）或者 \(\nu=0\) 已到达消除不等式约束以及使得拉格朗日函数和原函数同时取得最优的目的。总结如下

\[\begin{cases} L_x^{\prime} = 0 \\ m_i(x) = 0 \ \& \ \lambda_i \ne 0 \\ \nu_j g_j(x) = 0 \end{cases} \]

此时拉格朗日函数和原函数完全等价。所以进行如下推导：

\[\begin{aligned} \because &\sum_{j=1}^n \nu_j n_j(x) \le 0 \quad \sum_{i=1}^m \lambda_i m_i(x)=0 \\ & \max \sum_{j=1}^n \nu_j n_j(x) = 0 \\ \therefore &\underset{\nu}{\max} L(x, \nu) = f(x) \\ \therefore& \underset{x}{\min} \underset{\nu}{\max} L(x, \nu)=\underset{x}{\min} f(x) \end{aligned} \]

整理一下便为 KKT 条件：

\[\begin{cases} m_i(x^*) = 0 \\ \nu_j^* n_j(x^*)=0 \\ \nu_j^* \ge 0 \\ \frac{\partial L(x^*,\nu ^*)}{\partial x} = 0 \end{cases} \]

弱对偶性的证明

弱对偶性是指：

\[\underset{x}{\min}\underset{\lambda, \nu}{\max}L(x,\lambda,\nu) \ge \underset{\lambda, \nu}{\max}\underset{x}{\min}L(x,\lambda,\nu) \]

这等价于证明“凤尾”是大于“鸡头”的。证明挺简单的如下：

\[\because \ \underset{x}{\min}L(x,\lambda,\nu) \le L(x,\lambda,\nu) \\ \therefore \ \underset{\lambda, \nu}{\max}\underset{x}{\min}L(x,\lambda,\nu) \le L(x,\lambda,\nu) \]

上式先变化 \(x\) 使 \(L\) 变到 \(x\) 能使其变到的最小的一个域。在这个域里面 \(\lambda, \nu\) 是可以任意变化的，但即便 \(\lambda, \nu\) 变化使其达到最大值也只是 \(\underset{x}{\min}L(x,\lambda,\nu)\) 的顶端了。可 \(\underset{x}{\min}L(x,\lambda,\nu)\) 整个域的所有取值可能都比 \(L(x,\lambda,\nu)\) 小，所以有 \(\underset{\lambda, \nu}{\max}\underset{x}{\min}L(x,\lambda,\nu) \le L(x,\lambda,\nu)\)
同理：

\[\because \ \underset{\lambda, \nu}{\max}L(x,\lambda,\nu) \ge L(x,\lambda,\nu) \\ \therefore \ \underset{x}{\min}\underset{\lambda, \nu}{\max}L(x,\lambda,\nu) \ge L(x,\lambda,\nu) \]

证毕

弱对偶性的几何证明

原问题可以简化为只有不等式约束的情况，因为满足最优解的时候同样需要满足等式约束才能使得拉格朗日函数等于原函数。于是有：

\[\begin{cases} \min f(x) \\ s.t. \ m_i(x) \le 0 \ (i = 1, 2,..., N) \end{cases} \]

于是可以得到拉格朗日函数为：

\[L(x, \lambda) = f(x) + \lambda m_i(x), \ \lambda \ge 0 \]

此时令

\[\begin{aligned} p^* &= \underset{x}{\min}f(x)=\underset{x}{\min}\underset{\lambda}{\max}L(x, \lambda) \\ \ d^* &= \underset{\lambda}{\max}\underset{x}{\min}L(x, \lambda) \end{aligned} \]

也就是说 $p^{*} $ 是原问题的最优解，而 \(d^{*}\) 是对偶问题的最优解。弱对偶性实际上指对偶问题的最优解是小于等于原问题的最优解的。

首先，令 \(f(x) = t,\ m_i(x) = u\)，于是得到由它们不同的取值而得到一个区域，称之为 \(G\)。定义如下：

\[G=\{(u,t)|x\in D\} \]

其中 \(D\) 是原问题的定义域，有了上述定义以后，便有：

\[p^* = \underset{x}{\min}f(x)=\underset{x}{\min}t=inf\{t|(u,t)\in G,u \le0\} \]

原问题即求 \(t\) 在 \(u \le 0\) 时的最小值。

 
 
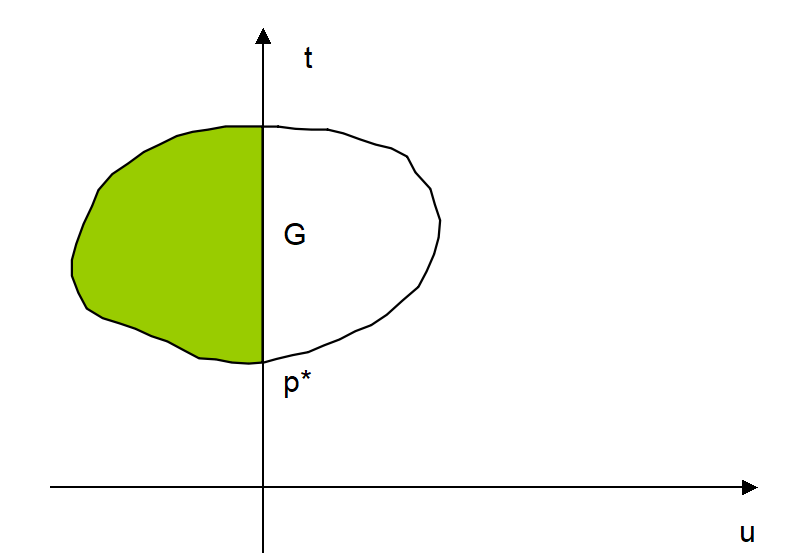
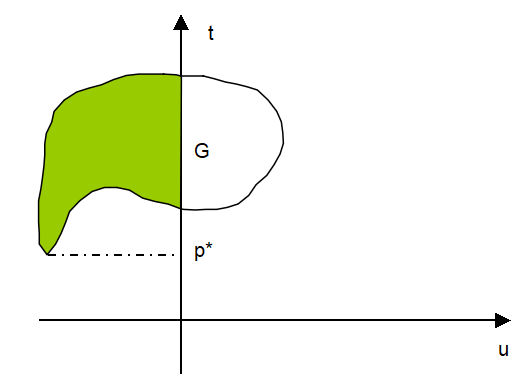
可视化后如上图所示，\(G\) 区域是白色区域和绿色区域的总和（即原问题的定义域），\(p^*\) 则是绿色区域 \((u \le 0)\) 的最低点(纵坐标最小的点)。此时对偶问题的最优解 \(d^*\) 转化到 \(G\) 区域为：

\[\begin{aligned} d^* &= \underset{\lambda}{\max} \underset{x}{\min} L(x, \lambda) \\ &=\underset{\lambda}{\max} \underset{x}{\min} \ t+\lambda u \end{aligned} \]

因此，对偶问题可以简化为：

\[\begin{aligned} g(\lambda) &= \underset{x}{\min} t + \lambda u \\ &= inf\{t+\lambda u|(u,t)\in G\} \\ d^* &= g_{max}(\lambda) \end{aligned} \]

对偶问题的最优解可以理解为在 \(g(\lambda)\) 的下确界中取得最大值。

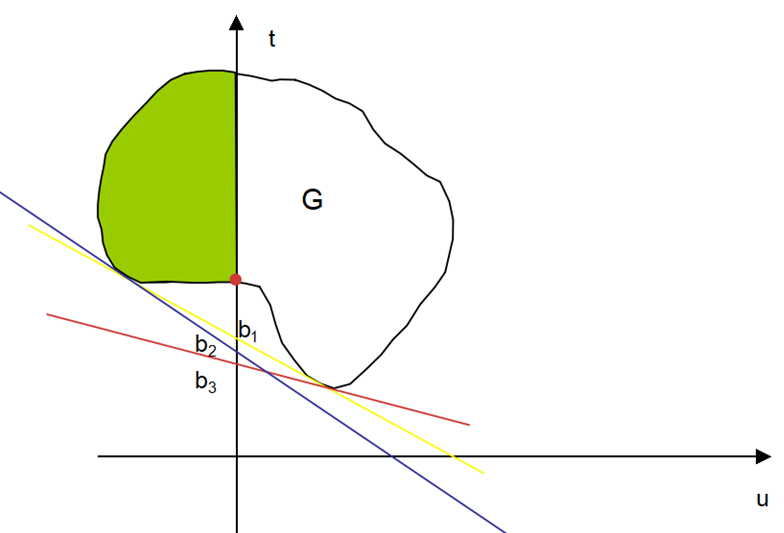
可以将 \(t+\lambda_i u = b_i\) 看作一条直线，首先对于某一 \(\lambda\) ，\(b\) 由许多不同的取值 \(b_i,i=1,2,...,N\) ，可以认为是许多斜率相同，但是截距不一样的直线（特别地，有\(\lambda \ge 0\) 所以 \(t+\lambda_i u = b_i\) 一定是斜率为负或者0的直线）。我们对于每个固定的 \(\lambda\) 取截距最小的那一条线，比如图中的红线，有很多条斜率与红线相同且与 \(G\) 区域有交集的直线，但这些直线中显然只有与 \(G\) 区域下端相切的直线（即红线）的截距是最小的。

于是我们得到各种不同 \(\lambda\) 中截距最小的直线，同时也得到相应的截距，如：\(b_1,b_2,b_3\) 。特别地当 \(G\) 是凹集的时候，与 \(G\) 下端有两个切点的直线的截距是所有截距中最大的，如：黄线的 \(b_1\) 。可能有人会问为什么不将蓝线绕切点逆时针旋转，可以获得更大的截距，答案：不行，因为我们在获得这些直线的时候，首先保证得是同斜率中截距最小，然后才是不同斜率中截距最大。单纯将蓝线旋转，将使得蓝线穿过 \(G\) 的白色区域，此时蓝线不是该斜率中截距最小的。（用一条标准衡量即可：所有不同斜率的直线来比较截距大小的，必然是跟 \(G\) 的交集是一个切点或者两个切点的直线）

此时最后筛选下来的最大截距 \(b_{max}\) 即为对偶问题的最优解 \(d^*\) ，\(d^*\) （图中为 \(b_1\))是小于原问题的最优解 \(p^*\) 的（绿色区域中最低点的纵坐标）

强对偶性的几何证明

 
 
 
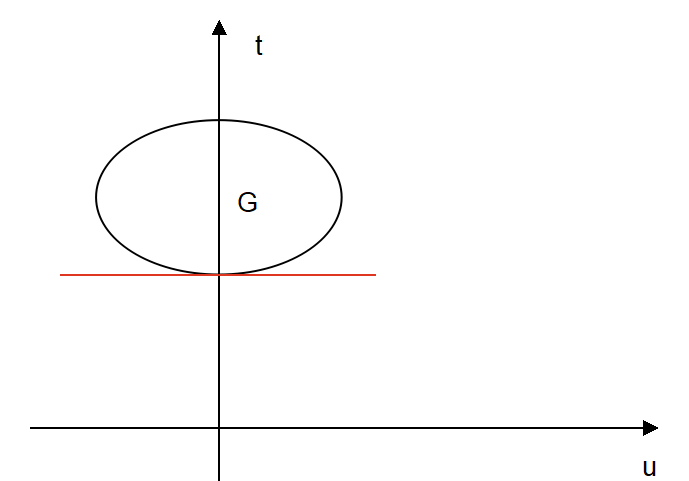
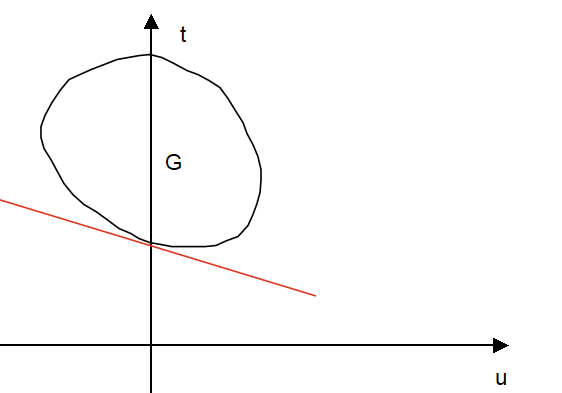
如果 \(G\) 是一个凸集（即原问题为凸优化问题），那么显然对偶问题的最优解和原问题的最优解均为绿色区域的最低点的纵坐标，即：\(p^*=d^*\) 此时具有强对偶性，如第一列的图和第二列的左图（一般来说 \(G\) 为凸集，就意味着强对偶性，但也不是绝对。当然 \(G\) 不是凸集也可能具有强对偶性如：第二列的右图。可以看得出来都是满足 KKT 条件的，KKT 条件为求得对偶问题解和原问题解的必要条件。

slater condition

定义：如果对于 \(x\) 的定义域 \(D\)，如果它存在一个内点 \(x^*\) 满足对于任意的 \(M_i(x) \lt 0\)，则说明该问题满足 slater 条件，其实也就是绿色区域部分需要有点存在。凸集加上 slater 条件即为强对偶性。