重要图像
\[\frac{1}{v}\cdot\Delta x=\Delta t\notag
\]
二项式展开
\[(x+\Delta x)^n=x^n+nx^{n-1}\Delta x+\frac{n(n-1)}{2}x^{n-2}(\Delta x)^2+...+(\Delta x)^n\notag
\]
求极值的2个思路
-
变分
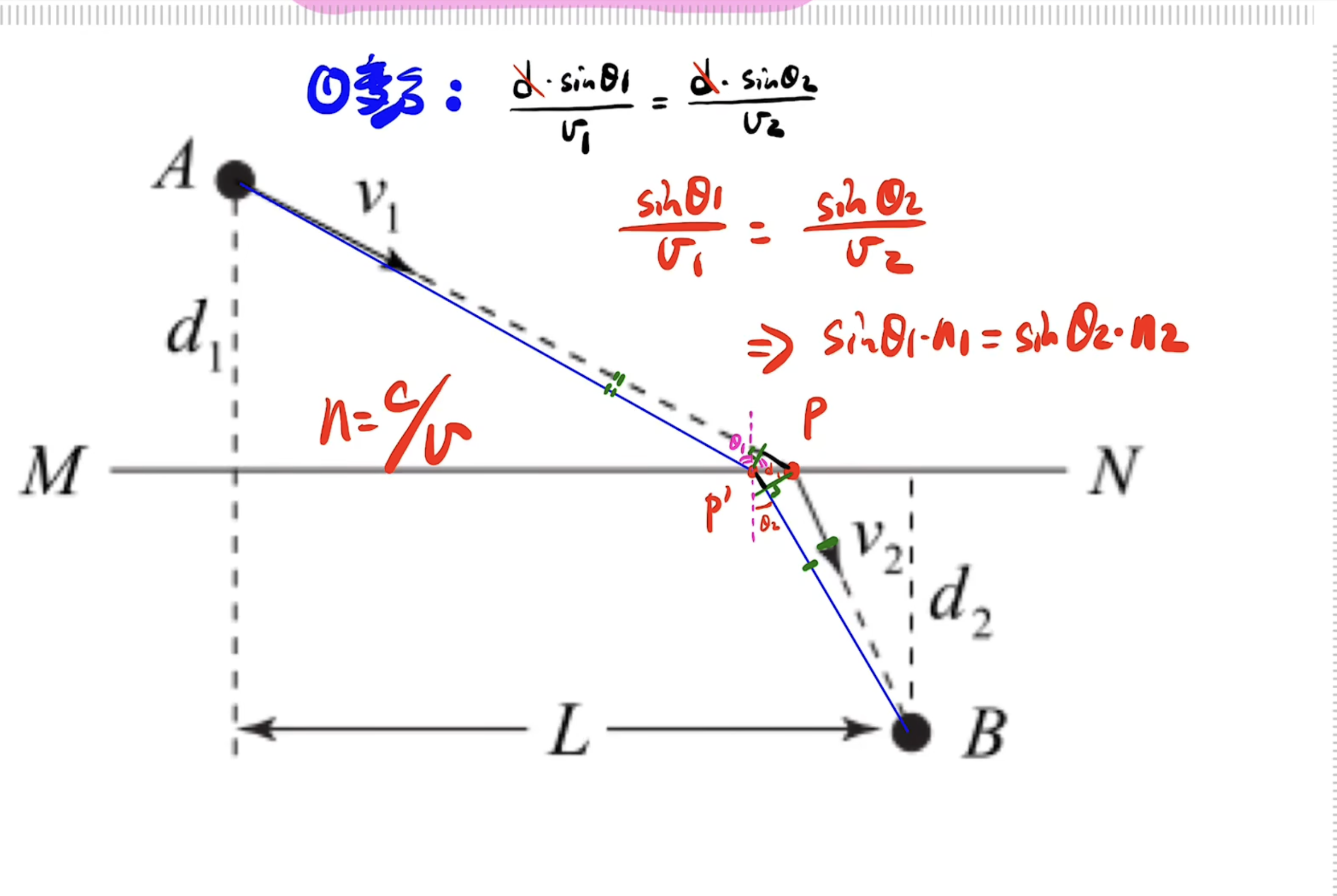
-
求导
斜抛运动的外包络线
\[y=\frac{v_0^2}{2g}-\frac{g}{2v_0^2}x^2
\]
证明
由抛体运动轨迹\(f(x,\theta)=x\tan\theta-\frac{g}{2v_0^2}(1+\tan^2\theta)x^2\)
\(y\)上的点可视为对于固定的\(x_0\),\(y=\max\{y_1\}\)
\(f(\theta)=x\tan\theta-\frac{g}{2v_0^2}(1+\tan^2\theta)x^2\)
整理得,\(f(\theta)=-\frac{gx^2}{2v_0^2}\tan^2\theta+x\tan\theta-\frac{gx^2}{2v_0^2}\)
故\(f(x,\theta)为抛物线,f(x,\theta)=\frac{v_0^2}{2g}-\frac{g}{2v_0^2}x^2\)
运用
常用于求极值

抛体结论
结论1
一个以给定的初速度\(v_0\),仰角为\(\theta\),抛出的物体的射程为\(S\)
易知以同样的初速度,仰角\(\theta _2=\pi/2-\theta _1\),抛出物体的射程也是\(S\),且射程相同的两个抛体在空中停留的时间
乘积\(t_1t_2=\frac{2S}{g}\)
结论2
以\(\vec v_0\)抛出一个物体,若要求射程的极值,可以考虑画出矢量三角形求面积
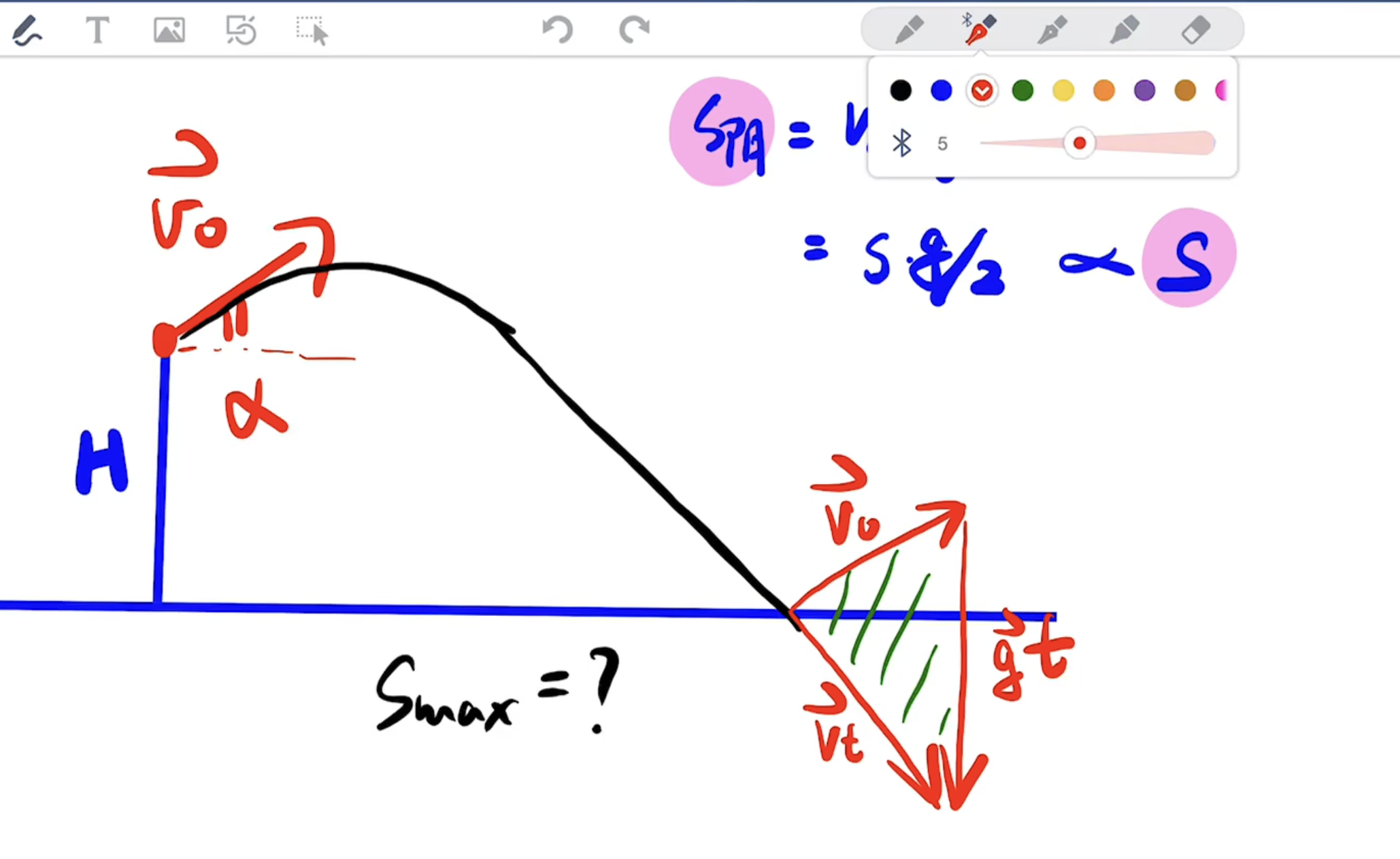
证明:
\[v_\parallel=v_0\cos\alpha+v_t\sin\alpha,\\
S_\triangle=\frac{gtv_\parallel}{2}\\
s=v_\parallel t,
\notag
\]
故\(s\)正比例于\(S_\triangle\)
求导积分公式
指数函数
\[(x^n)'=n\cdot x^{n-1}\tag 1
\]
\[\int x^n{\rm d}x=\frac{1}{n+1}x^{n+1}+C (n\neq -1)\tag 2
\]
三角函数
\[(\sin x)' = \cos x\tag1
\]
\[\int{\sin x {\rm d}x } = -\cos x + C\tag2
\]
\[(\cos x)' = -\sin x + C\tag3
\]
\[\int{\cos x {\rm d}x} = \sin x + C\tag4
\]
自然指对
\[(e^x)' = e^x \tag 1
\]
\[\int{e^x {\rm d} x} = e^x + C \tag 2
\]
\[(\ln x)' = \frac{1}{x} \tag 3
\]
\[\int{\frac{1}{x} {\rm d} x} = \ln{|x|} + C\tag4
\]
证明:
\[y=\ln x\tag1
\]
\[x=e^y\tag2
\]
\[\frac{{\rm d}x}{{\rm d}y} = e^y\tag3
\]
\[\frac{{\rm d}y}{{\rm d}x} = \frac{1}{e^y}\tag4
\]
代入\(e^y=x\)
\[\frac{{\rm d}y}{{\rm d}x} = \frac{1}{x}\tag5
\]
极坐标系下的圆周运动
设运动方程\(r(t) = vt\),\(\theta (t) = \omega t\)
故\(v\)可以分成\(v_n\)和\(v_\tau\)
\[v_n = \dot{r},v_\tau = r\cdot \dot{\theta}\tag 1
\]
\[a_n = \ddot{r} - \dot{\theta}^2\dot r,a_tau = \ddot{\theta}r + 2\dot{\theta}\cdot \dot{r} \tag2
\]
相对运动
(角标传递性)
-
\[\vec v_{B\rightarrow A}=\vec v_B-\vec v_A
\]
就像人感觉风从哪来
-
\[\vec v_{A}=\vec{v_{A\rightarrow O}}+\vec{v_{O\rightarrow 地}}
\]
相对+跟随=绝对
自然坐标系
如何理解
没有固定的坐标轴
\[\vec{r},\vec{v} = \frac{{\rm d}\vec{r}}{{\rm d}t},\vec{a} = \frac{{\rm d}\vec{v}}{{\rm d}t}
\]
曲率半径
二次函数的曲率半径
试确定抛物线\(y=ax^2\)在\(x=0\)处的曲率半径
由平抛规律得出
\[x=v_0t\tag1
\]
\[y=\frac{1}{2}gt^2\tag2
\]
消去时间\(t\)得出曲线方程
\[y=\frac{1}{2}g(\frac{x}{v_0})^2\tag3
\]
由于\(a_n = g\),代入\(a_n = \frac{v^2}{\rho}\),得
\[\rho=\frac{v_0^2}{g}\tag4
\]
对比系数\(\frac{g}{2v_0^2}=a\),得
\[\rho = \frac{1}{2a}\tag5
\]
一般函数的曲率半径
由于上述方法使用了待定系数的方法,只适用于已知二次函数的情况.
现给出一种更加一般的方法

已知函数\(y=y(x)\)
将它改写成运动学中的参数方程
\[y=y(t)\tag1
\]
\[x = t\tag2
\]
任意选取函数上的一点\(P\),做出切线,即为\(\vec{v}\)的方向,做出矢量三角形,\(v\)在x轴上的分量为1,因为\(\dot{x}=1\)y轴上的分量为\(\dot{y}\)
设\(\vec{v}\)与水平方向的夹角为\(\theta\),则\(\tan\theta = \dot{y}\)
做出\(P\)点加速度,方向竖直向上,因为\(\ddot{x}=0\),也就是只有y轴上的分量,将其分解为\(a_n\)和\(a_\tau\),由相似三角形可知
\[a_n = \ddot{y} \cos \theta \tag1
\]
\[a_n = \frac{v^2}{\rho} \tag2
\]
\[\cos \theta = \frac{1}{v} \tag3
\]
联立解得
\[\rho = \frac{v^2}{\ddot{y} \cos \theta} = \frac{v^3}{\ddot{y}} = \frac{(\dot{y}^2 + 1)^{3/2}}{|\ddot{y}|}
\]
加绝对值是因为导数有可能为负,而曲率半径为正.
瞬心
做纯滚动时点\(P\)运动到最下面时,易证瞬时速度为\(0\)(不然就产生了滑动,也可用相似三角形证明),于是可看做圆上的所有点都围绕着这个瞬心\(P\)转动
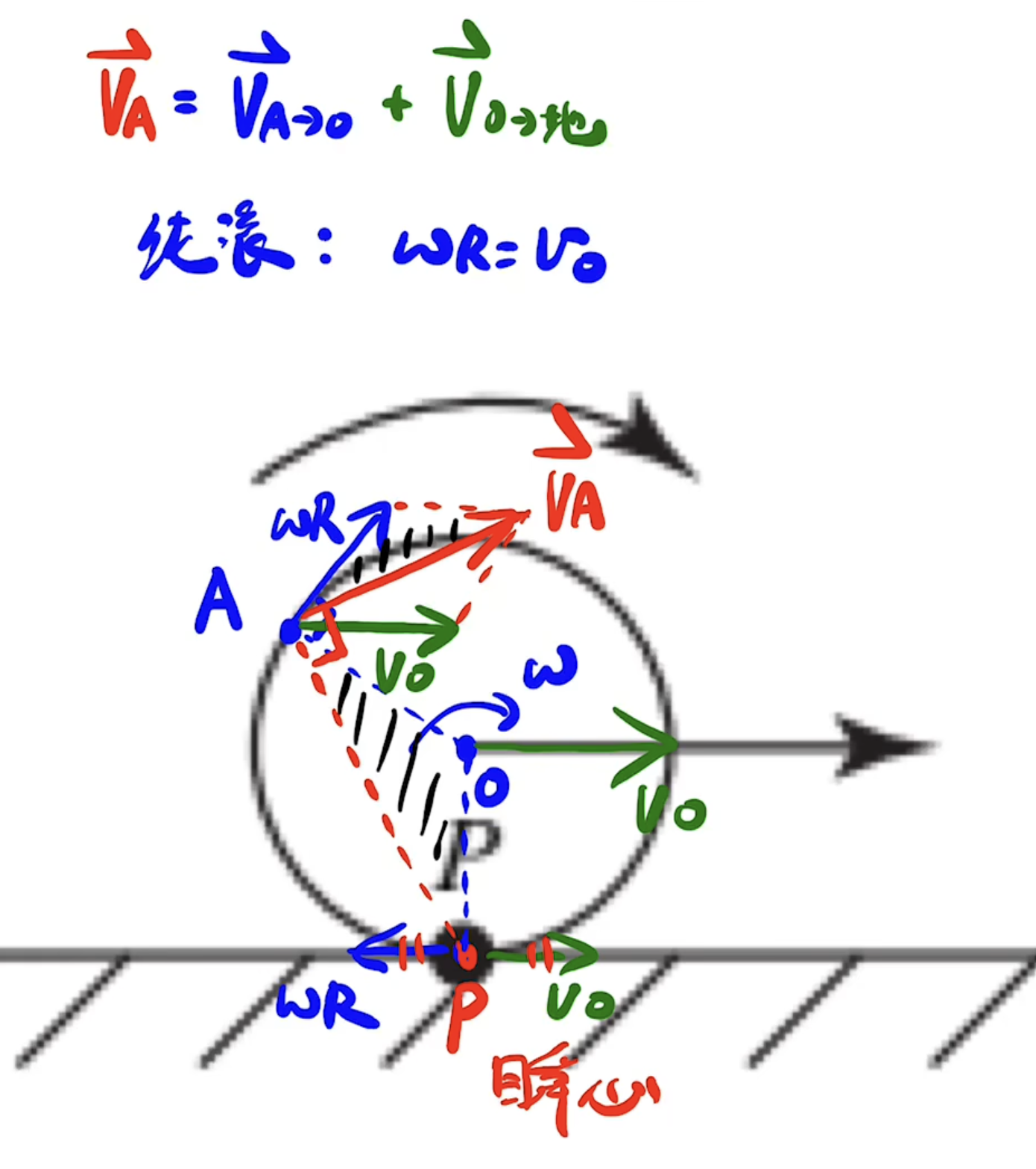
\[\frac{\pi}{2} - \arcsin \alpha = \arccos \alpha
\]
角加速度
定义
\[\beta = \frac{{\rm d}\omega}{{\rm d}t}(rad/s^2) \tag1
\]
\[\omega(t) = \omega_0+\beta t,\theta(t) = \omega_0t+\frac{1}{2}\beta t^2 \tag2
\]
\[a_\tau = \beta r \tag3
\]
匀角加速度运动特点
- \(\vec{a}\)方向逐渐靠近\(a_n\)
- \(a_\tau\)不变
解微分方程步骤
- 分离变量
- 两边积分
换系证明碰撞问题
假设有一个小球\(A\)以\(v_0\)向\(B\)球撞去,\(B\)一开始静止,二者质量都为\(m\),求碰撞后二者速度
动量守恒
显然,碰撞前后动量,机械能守恒
\[\frac{1}{2}mv_0^2=\frac{1}{2}mv_A'^2+\frac{1}{2}mv_B'^2\tag1
\]
\[mv_0=mv_A'+mv_B'\tag2
\]
联立,解得\(v_A'=0,v_B'=\frac{1}{2}v_0\)
质心系
算出质心系速度
\[v_c = \frac{\displaystyle \sum_{i=1}^{n}m_iv_i}{\displaystyle \sum_{i=1}^{n}m_i}=\frac{v_0}{2}
\]
记为C系
\(A\)对于C系速度\(v_{A\rightarrow C}=v_A-v_C=\frac{v_0}{2}\)
\(B\)对于C系速度\(v_{B\rightarrow C}=v_B-v_C=\frac{-v_0}{2}\)
所以现在两边是对称情况,显然在C系中速度等大反向
然后换回地面参考系可知\(v_A'=0,v_B'=\frac{1}{2}v_0\)
关于质心的补充
\[x_c = \frac{\displaystyle \sum_{i=1}^{n}m_ix_i}{\displaystyle \sum_{i=1}^{n}m_i}\tag1
\]
\[v_c = \frac{\displaystyle \sum_{i=1}^{n}m_iv_i}{\displaystyle \sum_{i=1}^{n}m_i}\tag2
\]
\[a_c = \frac{\displaystyle \sum_{i=1}^{n}m_ia_i}{\displaystyle \sum_{i=1}^{n}m_i}\tag3
\]







 浙公网安备 33010602011771号
浙公网安备 33010602011771号