NOIP2009提高组 最优贸易 详解（分层图状态转移 + SPFA）

分层图状态转移 + SPFA

 

洛谷  P1073

链接：https://www.luogu.org/problemnew/show/1073

 

其实此题可以不用强连通分量缩点，还有更优美的解法，只需60行代码

主要思想是类似“分层图”，或者类似“DAG”（有向无环图）的状态转移思想，特别是针对这种状态量相互影响的问题，分层图思想很实用。

分析

读完这道题，可以发现这样的事实：

• 你可以在图上任意走动

• 最终答案只与你的买入与卖出价格有关（我们就把买入卖出价值作为边权）

• 如果你买入了一个水晶球，你是没有不卖它的道理的（显然咯，买了不卖血亏...）

n平方的算法不难得出：

我只关心我在哪里买了这个水晶球，在哪里把它卖出去，并且，我能否从起点走到我的买入点，从买入点走到卖出点，然后在走到n

因此，先枚举两个点再bfs检查能否到达，然后更新答案。

而此题的难点在与你如何知道你是否能够到达买入，卖出，钟点（即上两行 并且 后面我说的话），和你能否把所有可能的情况考虑在内。

分层图可以很好的解决这个问题。

由于可以任意走动，所以我们可以建一张图，令图上的边全都是0，表示我的走动对我最终的结果没有影响。

考虑某个点 i ，它买入或者卖出水晶球的花费是v[i] 。

那么 当我们进行买入操作，我们就建立一条有向边转移到一张新图上，边的大小为-v[i]，指向点i所能到达的点（在第二层图上）而这张新图就是我们的第二层图。

它表示：假如我选择走了这条边，就是我在这个点买了这个水晶球，我不会反悔，并且我接下来考虑在某个点卖它。

当我们进行卖出操作，我们建立一条有向边转移到第三层图上，边的大小为v[i]，指向i所能到达的点（在第三层图上）。

它表示：假如我选择走了这条边，就是我在这个点卖了这个水晶球，我不会反悔，并且我接下来考虑走向终点。

可以发现，从第一层图走到第二层图走到第三层图走到终点，这就是一个合法的选择，而且分层图把所有可能的决策都考虑到了。

最后走向终点，我们有两种合法的操作：

• 不买卖直接走向终点

直接在第一层图的n号节点建立边权为0的有向边接入一个“超级终点”

• 买卖一次后走向终点

在第三层图的n号节点建立边权为0的有向边接入“超级终点”

最后解释一下为什么我们要分层：

因为当你分了层，你就可以从还未买入这个状态，转移到已经买入准备卖出这个状态，然后在转移到从卖出点走向终点的状态。由于有向边的建立，你不能从第二/三层走回第一层图，这保证了你只做一次买卖，而不是无限做买卖，符合了题目的要求

而我们最终的答案，就是求从第一层图的1号点，经过三层图走到“超级终点”的最长路,如图所示。

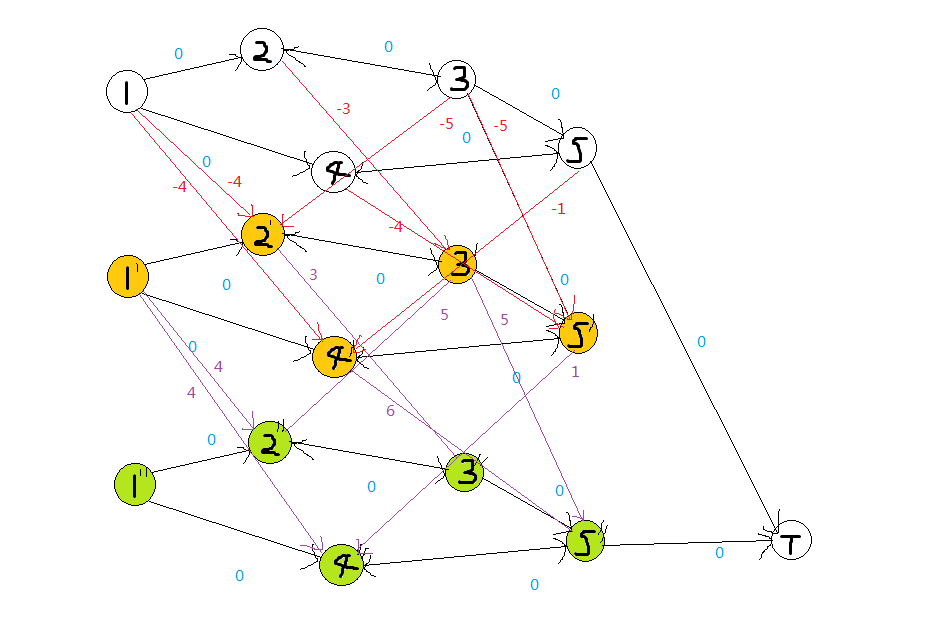
到此，本题就解完了

附代码

#include<bits/stdc++.h>
using namespace std;
#define oo 1<<18;
const int maxn = 100010;
struct u {
    int v,len; 
};
int n, m, v[maxn], d[maxn*3+1];
vector<u> G[maxn*3+1];

void addedge(int x,int y) {
  G[x].push_back((u){y,0});
  G[x+n].push_back((u){y+n,0});//第二层图我从n+1到2n进行编号 
  G[x+2*n].push_back((u){y+2*n,0});//第三层图我从2*n+1到3*n进行编号 
  G[x].push_back((u){y+n,-v[x]});
  G[x+n].push_back((u){y+2*n,v[x]});
  return;
}

queue<int> Q;
bool inq[maxn*3+1];

void spfa() {
  for(int i = 1;i <= n;i++)    d[i] = -oo;
  d[1] = 0;
  inq[1] = true;
  Q.push(1);
  while(!Q.empty()) {
      int tp = Q.front(); Q.pop();
      inq[tp] = false;
      int len = G[tp].size();
      for(int i = 0;i < len;i++) {
          u x = G[tp][i];
          if(d[x.v] < d[tp] + x.len) {
              d[x.v] = d[tp] + x.len;
              if(inq[x.v] == false) {
                  Q.push(x.v);
          inq[x.v] = true;
              }
          } 
      }
  }
}

int main() {
//    freopen("d.txt","r",stdin);  调试用的 
    cin >> n >> m;
    for(int i = 1;i <= n;i++) cin >> v[i];
    for(int i = 1,x,y,z;i <= m;i++) {
        cin >> x >> y >> z;
        addedge(x,y);
        if(z == 2) addedge(y,x);
    }
    G[n].push_back((u){3*n+1,0});
    G[n*3].push_back((u){3*n+1,0});//超级终点是3*n+1编号 
    n = 3*n + 1; //把n改成超级终点的编号，方便spfa操作 

    spfa();
    cout << d[n] << endl;
    return 0;
}