[详解]图论模型转化的思维题：AGC017E - Jigsaw

Problem Statement

We have \(N\) irregular jigsaw pieces. Each piece is composed of three rectangular parts of width \(1\) and various heights joined together. More specifically:

• The \(i\)-th piece is a part of height \(H\), with another part of height \(A_i\) joined to the left, and yet another part of height \(B_i\) joined to the right, as shown below. Here, the bottom sides of the left and right parts are respectively at \(C_i\) and \(D_i\) units length above the bottom side of the center part.

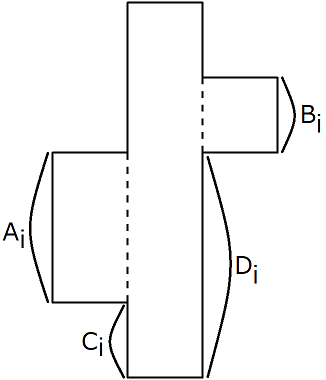
Snuke is arranging these pieces on a square table of side \(10^{100}\). Here, the following conditions must be held:

• All pieces must be put on the table.
• The entire bottom side of the center part of each piece must touch the front side of the table.
• The entire bottom side of the non-center parts of each piece must either touch the front side of the table, or touch the top side of a part of some other piece.
• The pieces must not be rotated or flipped.

Determine whether such an arrangement is possible.

Constraints

• \(1 \leq N \leq 100000\)
• \(1 \leq H \leq 200\)
• \(1 \leq A_i \leq H\)
• \(1 \leq B_i \leq H\)
• \(0 \leq C_i \leq H - A_i\)
• \(0 \leq D_i \leq H - B_i\)
• All input values are integers.

Solution

首先，该模型的可行性无法快速检验，我们必须将它转换为我们能处理的模型。

考虑用图论模型刻画可行性：用一条有向边\((l,r)\)刻画一个拼图，需要满足：积木\((l,r)\)右边能够有拼图\((l',r')\)等价于\(r=l'\)。

原题的限制

我们发现：积木的边界有两种情况：直接着地或不直接着地，分别对应\(C\)与\(D\)是否等于\(0\)。需要分情况讨论。

积木\((A,B,C,D)\)右边能够有拼图\((A',B',C',D')\)当且仅当：

• \(D = 0\)且\(B = C'\)，或
• \(C' = 0\)且\(D = A'\)，或
• \(D = 0\)且\(C' = 0\)。

最后一种很难刻画成边的连通的形态，所以我们暂时舍弃这一条。

一条路径的合法当且仅当：

• 最左边的拼图的\(C=0\)，且
• 最右边的拼图的\(D=0\)。

图论模型的构造与探索

经过试验，发现可以这么定义：（点的编号为\(-H,\dots,-1\)与\(1,\dots,H\)）

• \(l=\)：
  • \(A_i\)，当\(C_i = 0\)时。
  • \(-C_i\)，当\(C_i\ne 0\)时。
• \(r=\)：
  • \(-B_i\)，当\(D_i = 0\)时。（注意负号在这里）
  • \(D_i\)，当\(D_i\ne 0\)时。

这样，一条满足题目要求的路径就是一条从正数通向负数的路径了。

问题转化为：一张图是否可以被拆成若干条这样的路径？

先考虑最明显的入度与出度的限制：

• 编号为正的顶点满足：出度>=入度。
• 编号为负的顶点满足：出度<=入度。

考虑一些极端情况：（对图来说：图中有若干连通分量；存在环、树等特殊图论模型）当图为环时，显然不存在这样的路径拆分。推而广之，我们发现对一切欧拉回路，都不存在这样的路径拆分。换句话说，对任何一个弱连通分量，都存在顶点使得出度!=入度。

再手玩了几个例子，发现这些应该是刻画可行性所需的所有必要条件了，我们通过构造一个可行解来证明它是充分的：

对每一个弱连通分量，找到第一个出度>入度的正数点（必定存在——为什么？）。一直向下走直到不能够走为止。此时必定停留在一个负数点（为什么？）。我们将这个路径抽出来，图的剩下部分依然满足我们之前所说的性质吗？倘若不满足，则此时整个图中必定有一个或多个欧拉回路（因为此时度数的限制依然满足）。由于图本来是弱连通的，则途中必定经过一个与某个欧拉回路相连接的点，我们将这个回路包括进我们的路径就行了。对所有的回路都执行这个操作之后，剩下的图（如果有的话）将依然满足这些性质。重复此操作即可构造出一个可行解。

至此，我们只需要对每个弱连通分量中的所有点检查一遍是否满足以上条件就行了。用并查集/DFS都可以。

https://atcoder.jp/contests/agc017/submissions/21464597