吴恩达神经网络和深度学习——神经网络的编程基础

一、逻辑回归(Logistic Regression)

1. 符号定义 ：

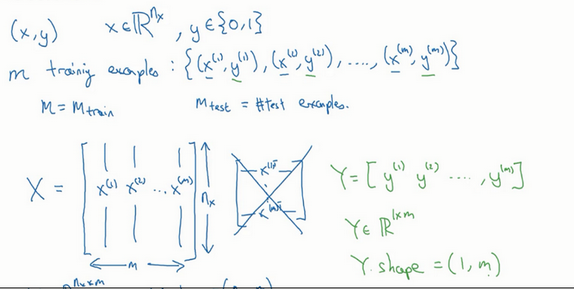
• x：表示一个n_x维数据，为输入数据，维度为(n_x，1)； 
• y：表示输出结果，取值为(0，1)；
• (x⁽ⁱ⁾，y⁽ⁱ⁾)：表示第i组数据，可能是训练数据，也可能是测试数据，此处默认为训练数据； 
• X=[x⁽¹⁾,x⁽²⁾,x⁽³⁾,...,x^(m)]：表示所有的训练数据集的输入值，放在一个 n_x  x m的矩阵中，其中m表示样本数目， X.shape等于（n_x ,m）; 
• Y=[y⁽¹⁾,y⁽²⁾,y⁽³⁾,...,y^(m)]：表示所有的训练数据集的输出值，放在一个 1  x m的矩阵中，其中m表示样本数目，Y.shape等于(1，m); 

　　用一对(x，y)来表示一个单独的样本，x代表n_x维的特征向量， y表示标签(输出结果)只能为0或1。 而训练集将由m个训练样本组成，其中(x^₍₁₎,y⁽¹⁾)表示第一个样本的输入和输出，(x^₍₂₎,y⁽²⁾)表示第二个样本的输入和输出，直到最后一个样本，然后所有的这些一起表示整个训练集。有时候为了强调这是训练样本的个数，会写作M_train，当涉及到测试集的时候，我们会使用来M_test表示测试集的样本

 

2. 假设函数Hypothesis Function

逻辑回归中，y_hat 表示y=1实际值为1的概率值，在0~1之间；使用线性模型，引入参数w和b，权重w的维度是（n_x ,1），b是一个常数项。

预测输出可以完成写成为：                                                                          sigmoid函数的一阶导数可以表示为：

  　　　　　　　　　　　　　　　　　　　　　　 

 

 

 

  

 

 

 

 

 

 

 

 

 

 

 

 

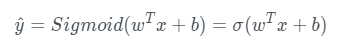
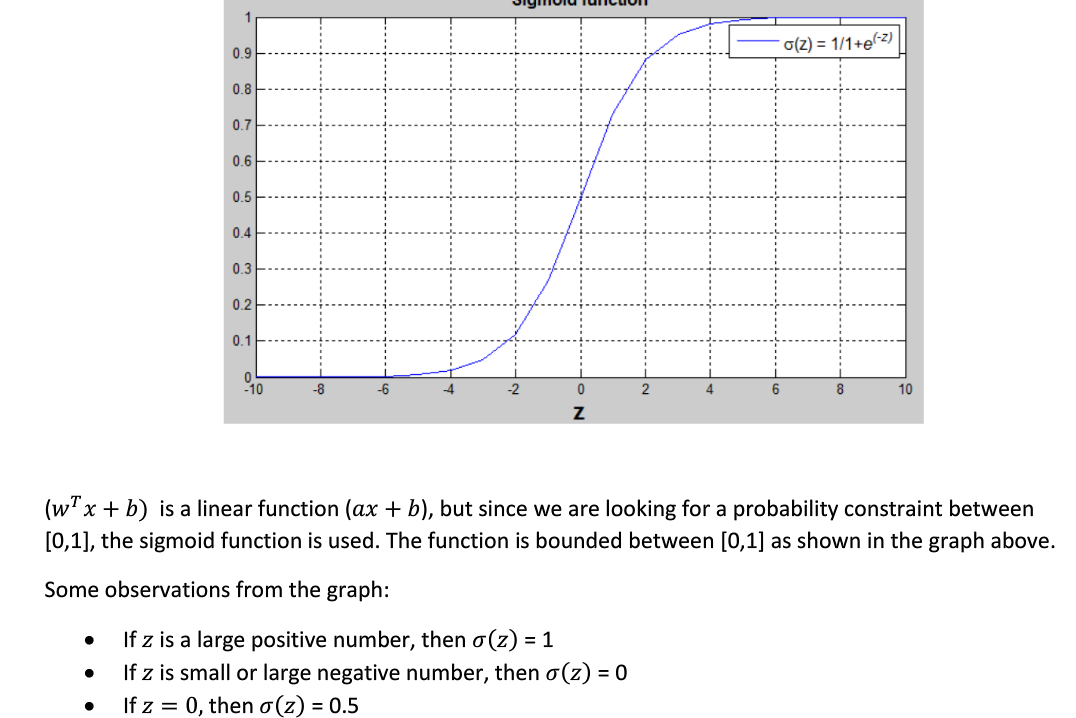
3. 代价函数（Cost Function）

 用于训练参数w和b，单个的代价函数用Loss function表示，线性回归一般使用平方误差函数，逻辑回归一般不适用，因为平方误差是非凸函数。

非凸函数在使用梯度下降算法时，容易得到局部最小值，而不是全局最优化。

对单个样本逻辑回归使用熵函数：

　

 

4. 梯度下降 

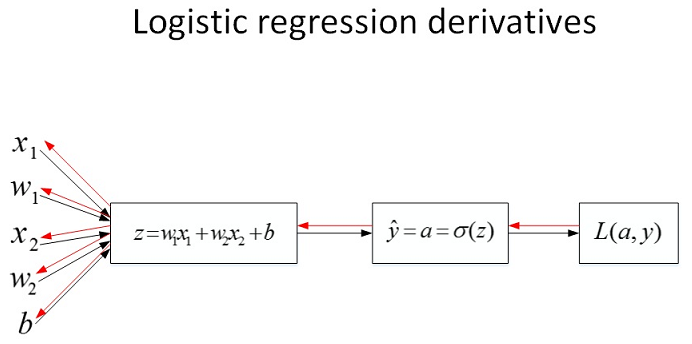
反向传播过程：

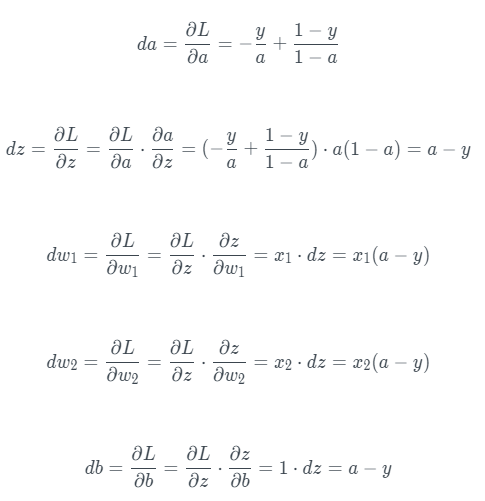
梯度下降算法表示为

                                                                    

                              

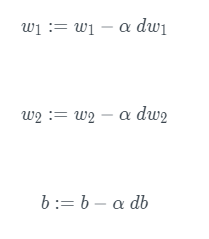
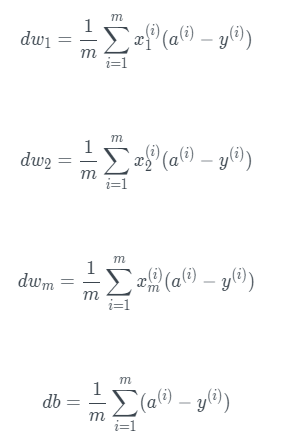
J=0; dw1=0; dw2=0; db=0;
for i = 1 to m
    z(i) = wx(i)+b;
    a(i) = sigmoid(z(i));
    J += -[y(i)log(a(i))+(1-y(i)）log(1-a(i));
    dz(i) = a(i)-y(i);
    dw1 += x1(i)dz(i);
    dw2 += x2(i)dz(i);
    db += dz(i);
J /= m;
dw1 /= m;
dw2 /= m;
db /= m;

6. 向量化梯度输出vectorization

 

 

 

Z = np.dot(w.T,X) + b
A = sigmoid(Z)
dZ = A-Y
dw = 1/m*np.dot(X,dZ.T)
db = 1/m*np.sum(dZ)

w = w - alpha*dw
b = b - alpha*db