线性代数学习笔记（1）--二维向量点积本质（仅供自己理解）

最近看了B站大神的视频，讲解线性代数一些概念的本质，其中P10讲到了点积，老师讲了点积的本质，当时由于水平不行不理解，重看了几遍，又自己捋了一下，并补充了一些证明，才弄明白。

在此整理备忘，没啥数学功底，表达起来相当困难，只能做到自己能看懂的程度，仅供自己以后回忆用。

 

首先，我觉得有一点必须提一下，摆正我的问题，之前我看视频的时候总在想 “为什么点积的本质是XXX”，而忘了点积其实是一个定义，是由数学家下的定义。

正确的提问方式应该是：点积被定义成这样，本质是什么。为什么本质是这个（用易于理解的证明方式，而非数学上的证明）。

这里只说二维向量

 

1、二维点积的定义

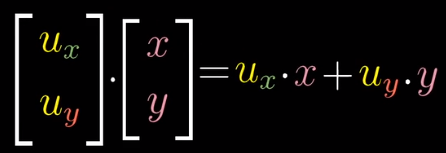
恰巧

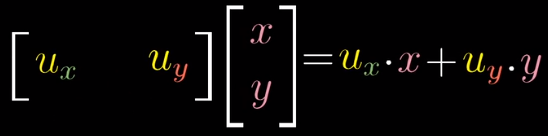
 点积意味着，将一个坐标分别为x和y的二维向量，线性变换到一个一维数轴上之后的长度，正负和它们的方向有关（结合前边的视频理解）。

 

 如果u向量的长度为1，即u帽，那么点积就是向量在上边投影的长度（视频中的一段阐述的大体意思）

 

 

 2、下边结合定义试着理解视频中阐述那段想表达的东西

 

 

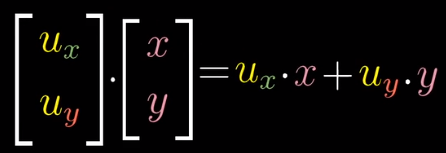
这个等式的右边就是它的定义，分成两个部分去理解，第一个就是加号两侧的这种表示怎么理解，第二个就是加号怎么理解。

 

2.1 加号两侧的这种表示怎么理解

  

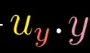
先从简单的解释，先把u向量的长度设为1(下称u帽），这样方便理解。因为，不管其它向量的方向如何，长度如何，都可以用它所在直线上的u向量，乘以一个倍数来表示

 

然后我们把x的坐标设为1即i帽，y的坐标设为1，即j帽，因为所有向量都可以由它们的两个基，各乘以倍数表示出来

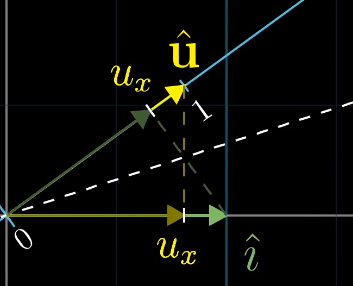
上图表明了u帽在i帽上的投影和i帽在u帽上的投影相等，因为i帽和u帽长度相等。这个长度就是u帽的x坐标值。

 

也就是说一个向量的x坐标X，用u帽做线性变换后，即X乘以i帽在u帽上的投影，而这个投影恰好是u帽的x坐标

 

即  X乘以u帽的x坐标  可以理解为X乘以i帽在u帽上的投影的长度，即u帽的x坐标，因为这和定义一致！

 

 

另外，这个表达式中点的左边正好是i帽在u帽上的投影，而这个表达式即代表着点积的左半部分，又代表着二维向量做一维向量变换的左半部分，

 

所以我们可以把i帽做u帽变换，理解为i帽投影到u帽上的长度。因为这和定义一致！！这就是定义想表达的含义。

 

u帽长度为1的时候，变换就是投影

对于j帽，即y坐标上的情况，和上边是一样的，不再赘述。

 

2.2 加号怎么理解

换句话说，为什么一个向量在u帽上的投影长度，等于它的x坐标在u帽上的投影长度 加上 y坐标在u帽上的投影长度

 

即，为什么 【x投影的长度】+【y投影的长度】=【这个向量在u帽上投影的长度】

 

这里需要一点容易理解的几何证明，强调一下，u帽的长度是1，如果u帽的长度不是1，那么就是投影的长度乘以一个倍数了。

 

其实就是证明以下内容：

 

 

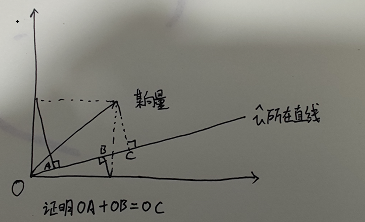
证明方式如下：

 图中的EF GH IJ都和OC垂直，是平行的，因此不难看出

OA:EF = OB:GH = OC:IJ

(OA+OB)/(EF+GH)=OC/IJ

图中的EF GH IJ都和OC垂直，是平行的，因此EFKI和GHJK都是平行四边形

显然EF+GH=IJ

所以OA+OB=OC

 

以上就是为什么有个加号