从最小割角度解决最大权闭合图问题及其在二分图形式下的优化

引入问题：

Kejin Game

UVALive - 7264

给出一张技能图，有的技能需要先置条件才能学习，而通过氪金可以取消某一些先置条件或者直接学习某一项技能，假设学习某项技能或者氪金都需要你付出一些代价，问代价最少为多少？

这个问题我写过了https://blog.csdn.net/baiyifeifei/article/details/83276927

解题思路

首先我们来审视某一个技能C，假设他存在先置技能A,B，那么我们使用一些原则来构建一张图：

假设一个技能直接习得的代价是D则在从该技能的入点向出点连接一条边；

假如一个技能是另一个的前置技能，那么就从前置技能的出点向待学习技能的入点连接一条边；

源点向所有技能的入点连接一条学习该技能所需的代价。

按照上面的法则，我们就可以构建出下面这样一张图

假使在ss，想要学习的技能的出点之间形成一个割，那么意味着这个技能就算被习得了。

以C为例，假设C想要脱离A这个前置的控制，那么就需要在Va，Dva，EDac之间任意选取一条边划去，同理取消B的限制也是一样的，再割裂Vc就算完全从正常学习的流程中学得了C技能了，当然也可以通过直接割裂Dvc这条边来达到形成割的目的

这题的思路并不难，但是把一个点和源点之间的关系割裂作为选择上了这个点的根据的做法提供了一种新的思路。

接着，我们来换一个问题，假设技能之间存在着如上面这个题目一样的依赖关系。现在每个技能存在一个权重，要求你学会一些技能使他们的权重尽可能大。

而这就是我们的“最大权闭合子图”

关于最大权闭合图：《最小割模型在信息学竞赛中的应用》

什么是最大权闭合子图？

给出一张图，图中的点与点之间通过有向边连接，选出一些点，保证这些选出的点的后继点也属于这些被选出来的点，且权值最大则是最大权闭合图。

如何寻找最大权闭合子图？

设立一个虚源点和一个虚汇点，所有的正权点都向虚源点连接容量为其权值的边，所有的负权点都向汇点连接容量为权值的边，原本有边的点之间连接容量无限大的边即可，最后权值之和减去这幅图的源点与汇点之间的最大流即可。

正确性：

我们知道最大流即是最小割，而这个模型中，我们只可能从与源点还有汇点连接的点去割，而其余的边由于容量无限，所以并不可能割，而这种割边的一端是源点或者汇点的割称作为简单割。

而可以证明的是对于一个网络N的简单割[S,T]与图G的闭合图V1方案存在一个对应关系 $V1\cup \left \{ s \right \}=S$ , $\overline{V1}\cup\left\{t\right\}=T$

证明：

闭合图对应简单割：由于V1闭合，所以V1与V2之间不存在边，s与t之间不存在边，所以 $V1\cup \left \{ s \right \}$ ， $\overline{V1}\cup\left\{t\right\}$ 之间也不存在边，所以，其就对应着割，而本图的所有割定为简单割，所以闭合图对应简单割

简单割对应闭合图：由于S，T为简单割，故S,T之间不存在边，而s，t之间也不存在边，故 $S-\left\{ s\right \}$ , $T-\left\{t \right \}$ 之间也不存在边，因而 $S-\left\{ s\right \}$ 图的所有后继点（除了s,t外）必然仍然在 $S-\left\{ s\right \}$ 内， $T-\left\{t \right \}$ 同理，所以简单割对应闭合图

这里我们再引入设一个点集V中的权值为正的点的集合为 $V_{ }^{+}$

最小割的流量

那么最小割[S,T]之间的割去的最小流量就是:

$c[S,T]=\sum_{v\in V_{2}^{+}}^{ }w_{v}+\sum_{v\in V_{1}^{-}}^{ }-w_{v}$

ps:[S,T]表示S,T之间的连边

证明：

$[S,T]=[\left \{ s \right \},V2]\cup [V2,V1]\cup[V1,\left \{ t \right \}]$

因为S，T为简单割，所以[V2,V1]为空集

因为只有正权与V1之间有连边，负权与V2之间有连边

所以：

$[\left \{ s \right \},V2]=[\left \{ s \right \},V_{2}^{+}]$

$[V1,\left \{ t \right \}]=[V_{1}^{-},\left \{ t \right \}]$

所以 $[S,T]=[\left \{ s \right \},V_{2}^{+}]\cup[V_{1}^{-},\left \{ t \right \}]$

所以 $c[S,T]=\sum_{v\in V_{2}^{+}}^{ }w_{v}+\sum_{v\in V_{1}^{-}}^{ }-w_{v}$

得证

如何保证得到的一定是最大权的闭合图？

最大权闭合图的总权重为：

$w(V_{1})=\sum_{v\in V_{1}^{+}}w_{v}-\sum_{v\in V_{1}^{-}}(-w_{v})$

令w(V1)+c[S,T]则有

$w(V_{1})+c[S,T]=\sum_{v\in V_{1}^{+}}w_{v}-\sum_{v\in V_{1}^{-}}(-w_{v})+\sum_{v\in V_{2}^{+}}^{ }w_{v}+\sum_{v\in V_{1}^{-}}^{ }-w_{v}$

$=\sum_{v\in V_{1}^{+}}w_{v}+\sum_{v\in V_{2}^{+}}w_{v}$

$=\sum_{v\in V_{ }^{+}}w_{v}$

经移项，得：

$ans=w(V1)=\sum_{v\in V_{ }^{+}}w_{v}-c[S,T]$

所以使正权和减去最小割既是答案的最大值

带二分图性质的最大权闭合图

当选择一条边两端的点时视作该边被选择，选择一条边，可以获得一个价值，选择点则需要付出一定的代价，问如何获得最大的价值。

例题最大获利 HYSBZ - 1497

设E为边，V为点，则问题的本质就变为：

$Maximize (\sum W_{E}-\sum W_{V})$

考虑到选了某条边，那么这条边的点就必选，其本质就变成了一个最大权闭合图问题，我们可以将边也抽象为点，向其两个端点连边，然后在这幅图上跑最大权闭合图即可，复杂度为O(MaxFlow(n+m,n+m))。

考虑上面这个问题，假如原图是一张稠密图（就如例题），那么这个算法的复杂度就会变得非常糟糕了，为此我们需要作出优化。

再来看这个式子

$Maximize (\sum W_{E}-\sum W_{V})$

我们可以通过乘上-1来使这个问题转化为求最小值

$Minimize(\sum W_{V}-W_{E})$

考虑到边的总价值等于所有的点相连的边的总价值减去那些已经选择的点和不选择的点之间的边除去2就是选择的边的总价值。也就是选择的点所连接的边的总价值减去与不选择的点之间的最小割/2，具体上可以看胡伯涛论文中的这幅图：

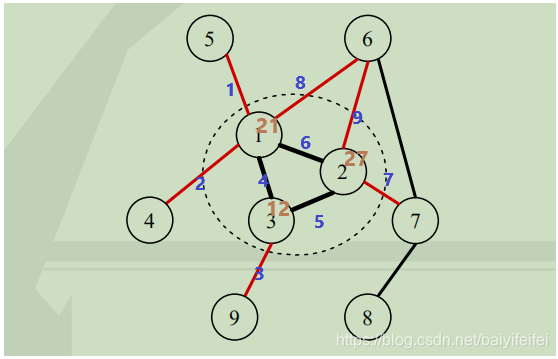
其中蓝紫色与棕色的数字是我自己标上的，其中蓝紫色的为边的价值，棕色的为与这个端点连接的边的价值之和，黑色加粗的边为选择的边，黑色虚线圆内的点（1,2,3）即是选择的边，我们不难发现图中选择的边的总价值就是

[(21+27+12)-(1+2+8+9+7+3)]/2=15

其中(1+2+8+9+7+3)也就是红色边的价值之和就是已选择的1,2,3与未选择的4,5,6,7.8,9之间的最小割

我们用 $W_{VE}$ 来表示与一点相连的所有的边的价值总和,已经选择的点集为V未选择的点集为V'，那么原式就可以表示为

$\sum W_{v}-\frac{\sum W_{vx}-c[V,V_{ }^{'}]}{2}$

进一步转化，原式就变成了

$\sum (W_{v}-\frac{W_{vx}}{2})+\frac{c[V,V_{'}]}{2}$

为了使得原式更加整齐，所以对原式乘2，那么原式就变成了

$\sum (2W_{v}-W_{vx})+c[V,V_{'}]$

因此原图中的每个点的权值就是 $2W_{v}-W_{vx}$ ，考虑最小割只能接受非负的边权，所以要为所有的点权加上一个极大值，令为U，然后答案就是 $\frac{U*n-C[S,T]}{2}$

可行性证明

$C[S,T]=\sum_{u\in S,v\in T}c_{u,v}$

$=\sum_{v\in \overline{V'}}C_{s,v}+\sum_{u\in V'}C_{u,t}+\sum_{u\in V',v\in \overline{V'},(u,v)\in E } C_{u,v}$

$=\sum_{v\in \overline{V'}}U+\sum_{u\in V'}(U+2W_{v}-W_{vx})+\sum_{u\in V',v\in \overline{V'},(u,v)\in E} W_{E}$

$=U|V|+\sum_{u\in V'}(2*W_{v}-W_{vx}+\sum_{v\in \overline{V'},(u,v)\in E}W_{E})$

$=U|V|+\sum_{u\in V'}(2*W_{V}-\sum_{v\in V',(u,v)\in E}W_{E})$

$=U*n+2\sum W_V-2\sum W_E$

$=U*n-2(\sum W_E-\sum W_E)$

$=U*n-2*ans$

所以 $ans=\frac{U*n-C[S,T]}{2}$

据此我们得到上面例题的解：

首先是直接暴力建图的超时答案：

/**************************************************************
    Problem: 1497
    User: FlyWhite
    Language: C++
    Result: Time_Limit_Exceed
****************************************************************/
 
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<string>
#include<map>
using namespace std;
const int maxn=60005;
const int maxm=3e5+5;
const int inf=0x3f3f3f3f;
struct Edge{
    int to,nxt,cap,flow;
}edge[maxm];
int tol;
int head[maxn];
void init(){
    tol=2;
    memset(head,-1,sizeof(head));
}
void addedge(int u,int v,int w,int rw=0){
    edge[tol].to=v;edge[tol].cap=w;edge[tol].flow=0;
    edge[tol].nxt=head[u];head[u]=tol++;
    edge[tol].to=u;edge[tol].cap=rw;edge[tol].flow=0;
    edge[tol].nxt=head[v];head[v]=tol++;
}
int Q[maxn];
int dep[maxn],cur[maxn],sta[maxn];
bool bfs(int s,int t,int n){
    int front=0,tail=0;
    memset(dep,-1,sizeof(dep[0])*(n+1));
    dep[s]=0;
    Q[tail++]=s;
    while(front<tail){
        int u=Q[front++];
        for(int i=head[u];i!=-1;i=edge[i].nxt){
            int v=edge[i].to;
            if(edge[i].cap>edge[i].flow&&dep[v]==-1){
                dep[v]=dep[u]+1;
                if(v==t) return true;
                Q[tail++]=v;
            }
        }
    }
    return false;
}
int dinic(int s,int t,int n){
    int maxflow=0;
    while(bfs(s,t,n)){
        for(int i=0;i<n;i++) cur[i]=head[i];
        int u=s,tail=0;
        while(cur[s]!=-1){
            if(u==t){
                int tp=inf;
                for(int i=tail-1;i>=0;i--)
                {
                    tp=min(tp,edge[sta[i]].cap-edge[sta[i]].flow);
                }
                maxflow+=tp;
                for(int i=tail-1;i>=0;i--){
                    edge[sta[i]].flow+=tp;
                    edge[sta[i]^1].flow-=tp;
                    if(edge[sta[i]].cap-edge[sta[i]].flow==0) tail=i;
                }
                u=edge[sta[tail]^1].to;
            }
            else if(cur[u]!=-1&&edge[cur[u]].cap>edge[cur[u]].flow&&dep[u]+1==dep[edge[cur[u]].to]){
                sta[tail++]=cur[u];
                u=edge[cur[u]].to;
            }
            else{
                while(u!=s&&cur[u]==-1) u=edge[sta[--tail]^1].to;
                cur[u] = edge [cur[u]].nxt;
            }
        }
    }
    return maxflow;
}
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    int ss=0,tt=n+m+1;
    init();
    for(int i=1;i<=n;i++)
    {
        int V;
        scanf("%d",&V);
        addedge(i,tt,V);
    }
    int W=0;
    for(int i=1;i<=m;i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        W+=w;
        addedge(ss,i+n,w);
        addedge(i+n,u,inf);
        addedge(i+n,v,inf);
    }
    printf("%d\n",W-dinic(ss,tt,tt+1));
}

下面是优化建图之后的AC代码：

/**************************************************************
    Problem: 1497
    User: FlyWhite
    Language: C++
    Result: Accepted
    Time:464 ms
    Memory:7388 kb
****************************************************************/
 
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<string>
#include<map>
using namespace std;
const int maxn=60005;
const int maxm=3e5+5;
const int inf=0x3f3f3f3f;
struct Edge{
    int to,nxt,cap,flow;
}edge[maxm];
int tol;
int head[maxn];
void init(){
    tol=2;
    memset(head,-1,sizeof(head));
}
void addedge(int u,int v,int w,int rw=0){
    edge[tol].to=v;edge[tol].cap=w;edge[tol].flow=0;
    edge[tol].nxt=head[u];head[u]=tol++;
    edge[tol].to=u;edge[tol].cap=rw;edge[tol].flow=0;
    edge[tol].nxt=head[v];head[v]=tol++;
}
int Q[maxn];
int dep[maxn],cur[maxn],sta[maxn];
bool bfs(int s,int t,int n){
    int front=0,tail=0;
    memset(dep,-1,sizeof(dep[0])*(n+1));
    dep[s]=0;
    Q[tail++]=s;
    while(front<tail){
        int u=Q[front++];
        for(int i=head[u];i!=-1;i=edge[i].nxt){
            int v=edge[i].to;
            if(edge[i].cap>edge[i].flow&&dep[v]==-1){
                dep[v]=dep[u]+1;
                if(v==t) return true;
                Q[tail++]=v;
            }
        }
    }
    return false;
}
int dinic(int s,int t,int n){
    int maxflow=0;
    while(bfs(s,t,n)){
        for(int i=0;i<n;i++) cur[i]=head[i];
        int u=s,tail=0;
        while(cur[s]!=-1){
            if(u==t){
                int tp=inf;
                for(int i=tail-1;i>=0;i--)
                {
                    tp=min(tp,edge[sta[i]].cap-edge[sta[i]].flow);
                }
                maxflow+=tp;
                for(int i=tail-1;i>=0;i--){
                    edge[sta[i]].flow+=tp;
                    edge[sta[i]^1].flow-=tp;
                    if(edge[sta[i]].cap-edge[sta[i]].flow==0) tail=i;
                }
                u=edge[sta[tail]^1].to;
            }
            else if(cur[u]!=-1&&edge[cur[u]].cap>edge[cur[u]].flow&&dep[u]+1==dep[edge[cur[u]].to]){
                sta[tail++]=cur[u];
                u=edge[cur[u]].to;
            }
            else{
                while(u!=s&&cur[u]==-1) u=edge[sta[--tail]^1].to;
                cur[u] = edge [cur[u]].nxt;
            }
        }
    }
    return maxflow;
}
int val[maxn]; 
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    memset(val,0,sizeof(val));
    int U=5e6+10;
    int ss=0,tt=n+1;
    init();
    for(int i=1;i<=n;i++)
    {
        int V;
        scanf("%d",&V);
        val[i]+=2*V;
        addedge(ss,i,U);
    }
    int W=0;
    for(int i=1;i<=m;i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        W+=w;
        val[u]-=w;
        val[v]-=w;
        addedge(u,v,w);
        addedge(v,u,w);
    }
    for(int i=1;i<=n;i++)
    {
        addedge(i,tt,val[i]+U);
    }
    printf("%d\n",(n*U-dinic(ss,tt,tt+1))/2);
}

最大密度子图

定义一个无向图的密度为边数|E|，除其点数|V|，即 $D=\frac{|E|}{|V|}$ ，给出一个无向图G=(V,E)，其具有最大密度的子图G=(V',E')称为最大密度子图。

我们设最大密度为Dmax那么就可以得出下式

$D_{max}\geqslant \frac{|E'|}{|V'|}$

$0\geqslant |E'|-D_{max}*|V'|$

我们令 $f(D)=|E'|-D*|V'|$ ,不难发现，当D>Dmax时，f(D)将小于0，D<Dmax时，f(D)将大于0，当D=Dmax时，f(D)=0

因此我们可以通过二分来确定D的值。接下来我们需要做的就是，在一个确定的D下maximize (f(D))

为此，我们将边权设为1，点权设为D再去跑上述的那个二分性质的最大权闭合子图即可。

例题： The Problem Needs 3D Arrays UVALive - 7037

AC代码（数据水，暴力建图）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<string>
#include<vector>
#include<map>
using namespace std;
const int maxn=8005;
const double eps=1e-8;
const int maxm=1000005;
const double inf=0x3f3f3f3f;
struct Edge{
	int to,nxt;
	double cap,flow;
}edge[maxm];
int tol;
int head[maxn];
void init(){
	tol=2;
	memset(head,-1,sizeof(head));
}
void addedge(int u,int v,double w,double rw=0.0){
	edge[tol].to=v;edge[tol].cap=w;edge[tol].flow=0;
	edge[tol].nxt=head[u];head[u]=tol++;
	edge[tol].to=u;edge[tol].cap=rw;edge[tol].flow=0;
	edge[tol].nxt=head[v];head[v]=tol++;
}
int Q[maxn];
int dep[maxn];
int cur[maxn];int sta[maxn];
bool bfs(int s,int t,int n){
	int front=0,tail=0;
	memset(dep,-1,sizeof(dep[0])*(n+1));
	dep[s]=0;
	Q[tail++]=s;
	while(front<tail){
		int u=Q[front++];
		for(int i=head[u];i!=-1;i=edge[i].nxt){
			int v=edge[i].to;
			if(edge[i].cap>edge[i].flow&&dep[v]==-1){
				dep[v]=dep[u]+1;
				if(v==t) return true;
				Q[tail++]=v;
			}
		}
	}
	return false;
}
double dinic(int s,int t,int n){
	double maxflow=0.0;
	while(bfs(s,t,n)){
		for(int i=0;i<n;i++) cur[i]=head[i];
		int u=s,tail=0;
		while(cur[s]!=-1){
			if(u==t){
				double tp=inf;
				for(int i=tail-1;i>=0;i--)
				{
					tp=min(tp,edge[sta[i]].cap-edge[sta[i]].flow);
				}
				maxflow+=tp;
				for(int i=tail-1;i>=0;i--){
					edge[sta[i]].flow+=tp;
					edge[sta[i]^1].flow-=tp;
					if(edge[sta[i]].cap-edge[sta[i]].flow==0) tail=i;
				}
				u=edge[sta[tail]^1].to;
			}
			else if(cur[u]!=-1&&edge[cur[u]].cap>edge[cur[u]].flow&&dep[u]+1==dep[edge[cur[u]].to]){
				sta[tail++]=cur[u];
				u=edge[cur[u]].to;
			}
			else{
				while(u!=s&&cur[u]==-1) u=edge[sta[--tail]^1].to;
				cur[u] = edge [cur[u]].nxt;
			}
		}
	}
	return maxflow;
}
pair<int,int> Ex[10005];
int cnt;
int n;
int ss,tt;
void build(double val)
{
	init();
	ss=0,tt=cnt+n+1;
	for(int i=1;i<=cnt;i++)
	{
		addedge(ss,i,1.0);
	}
	for(int i=1;i<=n;i++) addedge(i+cnt,tt,val);
	for(int i=1;i<=cnt;i++)
	{
		addedge(i,cnt+Ex[i].first,inf);
		addedge(i,cnt+Ex[i].second,inf);
	}
}
bool check(double mid)
{
	return 1.0*cnt-dinic(ss,tt,tt+1)>=eps;
}
int arr[105];

int main()
{
	int t;
	scanf("%d",&t);
	int kace = 1;
	while(t--)
	{
		printf("Case #%d: ",kace++);
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
		{
			scanf("%d",&arr[i]);
		}
		cnt=0;
		for(int i=1;i<=n;i++)
		{
			for(int j=1+i;j<=n;j++)
			{
				if(arr[j]<arr[i])
				{
					Ex[++cnt]=pair<int,int>(i,j);
				}
			}
		}
		double L=0,R=cnt;
		while(R-L>eps)
		{
			double mid=(R+L)/2;
			build(mid);
			if(check(mid)) L=mid;
			else R=mid;
		}
		printf("%.12f\n",L);
	}
}

posted @ 2018-11-10 01:00 Fly_White 阅读(128) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Fly_White