树链剖分
树链剖分的思想及能解决的问题
树链剖分用于将树分割成若干条链的形式,以维护树上路径的信息。
具体来说,将整棵树剖分为若干条链,使它组合成线性结构,然后用其他的数据结构维护信息。
树链剖分(树剖/链剖)有多种形式,如 重链剖分,长链剖分 和用于 Link/cut Tree 的剖分(有时被称作“实链剖分”),大多数情况下(没有特别说明时),“树链剖分”都指“重链剖分”。
重链剖分可以将树上的任意一条路径划分成不超过 条连续的链,每条链上的点深度互不相同(即是自底向上的一条链,链上所有点的 LCA 为链的一个端点)。
重链剖分还能保证划分出的每条链上的节点 DFS 序连续,因此可以方便地用一些维护序列的数据结构(如线段树)来维护树上路径的信息。
如:
修改 树上两点之间的路径上 所有点的值。
查询 树上两点之间的路径上 节点权值的 和/极值/其它(在序列上可以用数据结构维护,便于合并的信息)。
除了配合数据结构来维护树上路径信息,树剖还可以用来 (且常数较小)地求 LCA。在某些题目中,还可以利用其性质来灵活地运用树剖。
概念
重儿子:子树大小最大的儿子。
轻儿子:除重儿子以外都是轻儿子。
重链:连接重儿子的边即重链,最高点不一定是重儿子。剩余单个点也构成重链。
轻链:连接轻儿子的边。
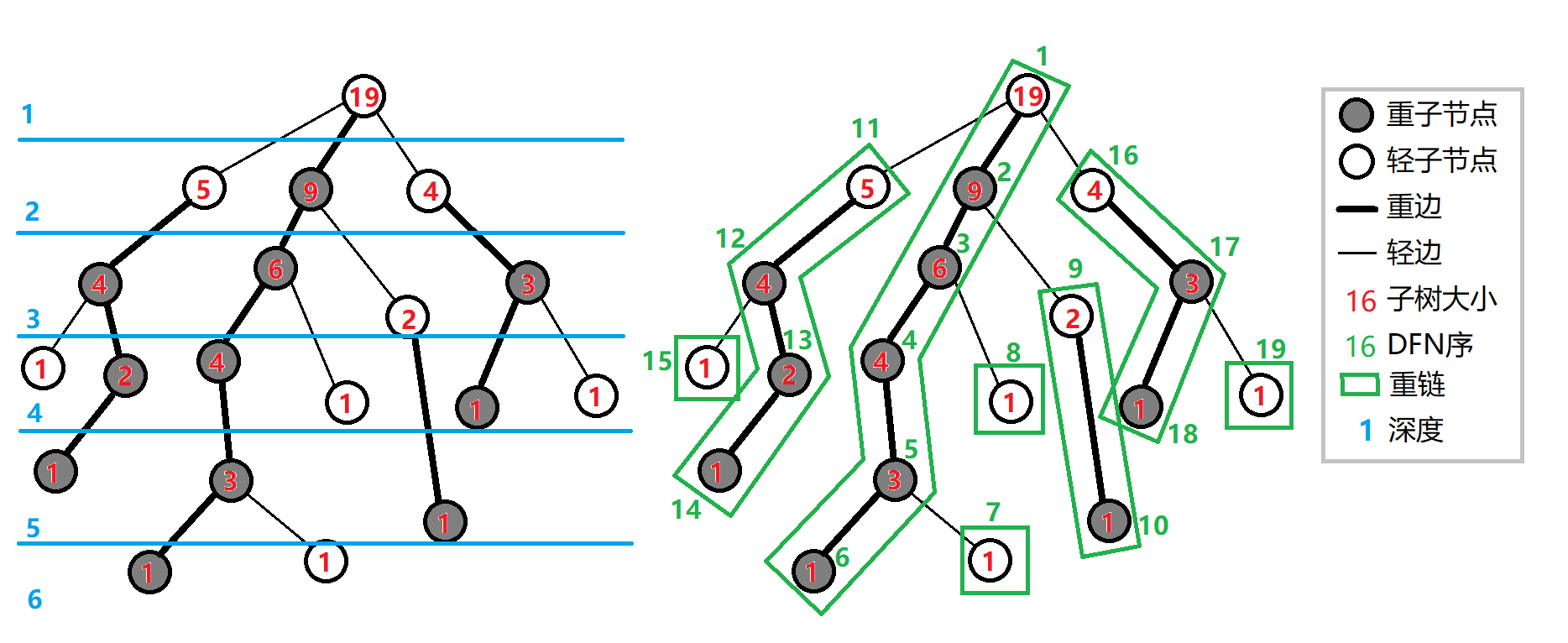
性质
-
树上每个节点都属于且仅属于一条重链。
-
重链开头的结点不一定是重子节点(因为重边是对于每一个结点都有定义的)。
-
所有的重链将整棵树 完全剖分。
-
在剖分时 重边优先遍历,最后树的 DFN 序上,重链内的 DFN 序是连续的。按 DFN 排序后的序列即为剖分后的链。
-
一颗子树内的 DFN 序是连续的。
-
可以发现,当我们向下经过一条 轻边 时,所在子树的大小至少会除以二。
-
因此,对于树上的任意一条路径,把它拆分成从 分别向两边往下走,分别最多走 次,因此,树上的每条路径都可以被拆分成不超过 条重链。
实现
我们可以通过两次dfs维护出dfs序,重儿子,重链,轻链,子树大小等。
int d[N]; //点的深度
int fa[N]; //点的父亲
int son[N];//重儿子
int sz[N]; //子树大小
int top[N];//重链顶端
int id[N];//dfs序
int cnt; //dfs序编号
int nw[N];//点权
void dfs1(int x,int fath)
{
d[x]=d[fath]+1,sz[x]=1,fa[x]=fath;
for(int i=head[x];i;i=ne[i])
{
int y=ver[i];
if(y==fath) continue;
dfs1(y,x);
val[y]=w[i];
sz[x]+=sz[y];
if(sz[son[x]]<sz[y]) son[x]=y;
}
}
我们选择优先进入重儿子来保证一条重链上各个节点dfs序连续,
一个点和它的重儿子处于同一条重链,所以重儿子所在重链的顶端还是t
void dfs2(int x,int t)
{
top[x]=t,id[x]=++cnt,nw[cnt]=val[x];
if(!son[x]) return;
dfs2(son[x],t); //优先遍历重儿子
for(int i=head[x];i;i=ne[i])
{
int y=ver[i];
if(y==fa[x]||y==son[x]) continue;
dfs2(y,y);
}
}
将树拆成链之后我们就可以用数据结构维护了,例如线段树维护区间最大最小,区间和。
struct tree
{
int l,r;
int sum;
int maxn;
int minn;
int lz;
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define maxn(x) t[x].maxn
#define minn(x) t[x].minn
#define lz(x) t[x].lz
}t[N*4];
void pushup(int p)
{
sum(p)=sum(p<<1)+sum(p<<1|1);
maxn(p)=max(maxn(p<<1),maxn(p<<1|1));
minn(p)=min(minn(p<<1),minn(p<<1|1));
}
void build(int p,int l,int r)
{
l(p)=l,r(p)=r;
if(l==r)
{
sum(p)=maxn(p)=minn(p)=nw[l];
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid),build(p<<1|1,mid+1,r);
pushup(p);
}
...
//主函数
n=read();
for(int i=1;i<n;i++)
{
int x,y,z;
x=read(),y=read(),z=read();
add(x,y,z);
add(y,x,z);
}
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
那我们如何求两点间路径上的信息呢?
我们可以用类似求lca的方法让两点“汇合”,具体如下。
让我们看看求LCA可以用什么算法:
倍增求LCA理论复杂度O(nmlogn)
Tarjian求LCA的理论复杂度是O(nm)
树链剖分了,理论复杂度最大为O(lognm),带个2的常数
既然如此优越,那就学习一下啊
int get_lca(int u,int v)
{
while(top[u]!=top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
u=fa[top[u]];
}
if(d[u]<d[v]) return u;
else return v;
}
我们让两端点中最深的一个跳到其所在重链顶端
问:为什么是最深的一个? 答:因为我们不能让某个点跳过它们的最近公共祖先。
问:为什么要直接跳到顶端? 答:节省时间,不用一个一个跳了。
问:每次这样跳它们会不会不能跳到一起? 答:的确,但它们最终可以跳到同一条重链上,(深度大的点就是原来两点的lca),都到同一条链上了我们要维护现在两点间的数据直接插入就可以了。
获取信息同理
int get_sum(int u,int v)
{
int res=0;
while(top[u]!=top[v]) //判断有没有到同一条重链上
{
if(d[top[u]]<d[top[v]]) swap(u,v);
res+=ask_sum(1,id[top[u]],id[u]);//显然,深度小的dfs序小所以它是左端点。
u=fa[top[u]]; //让深度大的往上跳
}
if(d[u]<d[v]) swap(u,v);
if(u!=v) res+=ask_sum(1,id[v]+1,id[u]);
return res;
}
聪明的小朋友现在应该已经掌握了树链剖分大法,快去做道例题试试吧。
例题
代码
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
const int N=2e5+10;
const int M=N*2;
const int INF=2147483647;
struct ee
{
int x,y;
}ip[N];
int n,m;
int tot;
int head[N],ver[M],ne[M],w[M];
void add(int x,int y,int z)
{
ver[++tot]=y;
ne[tot]=head[x];
head[x]=tot;
w[tot]=z;
}
int d[N];
int fa[N];
int son[N];
int sz[N];
int val[N];
void dfs1(int x,int fath)
{
d[x]=d[fath]+1,sz[x]=1,fa[x]=fath;
for(int i=head[x];i;i=ne[i])
{
int y=ver[i];
if(y==fath) continue;
dfs1(y,x);
val[y]=w[i];
sz[x]+=sz[y];
if(sz[son[x]]<sz[y]) son[x]=y;
}
}
int top[N];
int id[N];
int cnt;
int nw[N];
void dfs2(int x,int t)
{
top[x]=t,id[x]=++cnt,nw[cnt]=val[x];
if(!son[x]) return;
dfs2(son[x],t);
for(int i=head[x];i;i=ne[i])
{
int y=ver[i];
if(y==fa[x]||y==son[x]) continue;
dfs2(y,y);
}
}
struct tree
{
int l,r;
int sum;
int maxn;
int minn;
int lz;
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define maxn(x) t[x].maxn
#define minn(x) t[x].minn
#define lz(x) t[x].lz
}t[N*4];
void pushup(int p)
{
sum(p)=sum(p<<1)+sum(p<<1|1);
maxn(p)=max(maxn(p<<1),maxn(p<<1|1));
minn(p)=min(minn(p<<1),minn(p<<1|1));
}
void pushdown(int p)
{
if(lz(p))
{
lz(p<<1)^=1;
lz(p<<1|1)^=1;
lz(p)=0;
sum(p<<1)=-sum(p<<1);
sum(p<<1|1)=-sum(p<<1|1);
maxn(p<<1)=-maxn(p<<1);
minn(p<<1)=-minn(p<<1);
swap(maxn(p<<1),minn(p<<1));
maxn(p<<1|1)=-maxn(p<<1|1);
minn(p<<1|1)=-minn(p<<1|1);
swap(maxn(p<<1|1),minn(p<<1|1));
}
}
void build(int p,int l,int r)
{
l(p)=l,r(p)=r;
if(l==r)
{
sum(p)=maxn(p)=minn(p)=nw[l];
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid),build(p<<1|1,mid+1,r);
pushup(p);
}
void change1(int p,int x,int d)
{
if(l(p)==r(p))
{
sum(p)=maxn(p)=minn(p)=d;
return;
}
pushdown(p);
int mid=(l(p)+r(p))>>1;
if(x<=mid) change1(p<<1,x,d);
if(x>mid) change1(p<<1|1,x,d);
pushup(p);
}
void change2(int p,int l,int r)
{
if(l<=l(p)&&r>=r(p))
{
lz(p)^=1;
sum(p)=-sum(p);
maxn(p)=-maxn(p);
minn(p)=-minn(p);
swap(maxn(p),minn(p));
return;
}
pushdown(p);
int mid=(l(p)+r(p))>>1;
if(l<=mid) change2(p<<1,l,r);
if(r>mid) change2(p<<1|1,l,r);
pushup(p);
}
int ask_sum(int p,int l,int r)
{
if(l<=l(p)&&r>=r(p)) return sum(p);
pushdown(p);
int mid=(l(p)+r(p))>>1;
int res=0;
if(l<=mid) res+=ask_sum(p<<1,l,r);
if(r>mid) res+=ask_sum(p<<1|1,l,r);
pushup(p);
return res;
}
int ask_max(int p,int l,int r)
{
if(l<=l(p)&&r>=r(p)) return maxn(p);
pushdown(p);
int mid=(l(p)+r(p))>>1;
int res=-INF;
if(l<=mid) res=max(res,ask_max(p<<1,l,r));
if(r>mid) res=max(res,ask_max(p<<1|1,l,r));
pushup(p);
return res;
}
int ask_min(int p,int l,int r)
{
if(l<=l(p)&&r>=r(p)) return minn(p);
pushdown(p);
int mid=(l(p)+r(p))>>1;
int res=INF;
if(l<=mid) res=min(res,ask_min(p<<1,l,r));
if(r>mid) res=min(res,ask_min(p<<1|1,l,r));
pushup(p);
return res;
}
int get_sum(int u,int v)
{
int res=0;
while(top[u]!=top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
res+=ask_sum(1,id[top[u]],id[u]);
u=fa[top[u]];
}
if(d[u]<d[v]) swap(u,v);
if(u!=v) res+=ask_sum(1,id[v]+1,id[u]);
return res;
}
int get_max(int u,int v)
{
int res=-INF;
while(top[u]!=top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
res=max(res,ask_max(1,id[top[u]],id[u]));
u=fa[top[u]];
}
if(d[u]<d[v]) swap(u,v);
if(u!=v) res=max(res,ask_max(1,id[v]+1,id[u]));
return res;
}
int get_min(int u,int v)
{
int res=INF;
while(top[u]!=top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
res=min(res,ask_min(1,id[top[u]],id[u]));
u=fa[top[u]];
}
if(d[u]<d[v]) swap(u,v);
if(u!=v) res=min(res,ask_min(1,id[v]+1,id[u]));
return res;
}
void modify(int u,int v)
{
while(top[u]!=top[v])
{
if(d[top[u]]<d[top[v]]) swap(u,v);
change2(1,id[top[u]],id[u]);
u=fa[top[u]];
}
if(d[u]<d[v]) swap(u,v);
if(u!=v) change2(1,id[v]+1,id[u]);
}
int main(){
n=read();
for(int i=1;i<n;i++)
{
int x,y,z;
x=read(),y=read(),z=read();
x++,y++;
add(x,y,z);
add(y,x,z);
ip[i].x=x,ip[i].y=y;
}
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
m=read();
while(m--)
{
string op;
int u,v,w;
cin>>op;
u=read();
v=read();
if(op=="C")
{
int temp;
if(d[ip[u].x]<d[ip[u].y]) temp=ip[u].y;
else temp=ip[u].x;
change1(1,id[temp],v);
}
else if(op=="N")
{
u++,v++;
modify(u,v);
}
else if(op=="SUM")
{
u++,v++;
printf("%d\n",get_sum(u,v));
}
else if(op=="MAX")
{
u++,v++;
printf("%d\n",get_max(u,v));
}
else if(op=="MIN")
{
u++,v++;
printf("%d\n",get_min(u,v));
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号