10.25日模考总结

本周进行了标准OI普及组模考测试

得分情况

题目名称	做法	预计得分	实际得分
最近相等元素位置	map	100	30
超时空旅行	模拟、枚举	100	100
ATM数数 Ⅲ	数学、等差数列	100	100
升级大师	贪心	100	20

做题流程

首先看到第一题，非常的简单，直接用一个map写出代码，但是我总是觉得会超时，就用vector了

接着第二题，以为是个搜索，但是他有要求，所以我就枚举每个任务，看看是走过去快还是传送快，传送是哪个店铺快，统计起来即可

随后是第三题，一看，哇哈哈哈，这道题目我在信友队面试上做过类似的，于是我直接快速写出代码，就完事了

接着第四题，看上去是个贪心或背包、搜索，但是数据量有一点点大，所以我就用枚举+优化写了一个代码提交了

赛后心得

王德发***，第一题TLE30，本来以为自己优化了一下可以过，反而弄巧成拙，map可以A，vector不行

第二题第三题都AC了

第四题，枚举TLE20分，感觉有点少，怪可惜的

题目讲解

T1

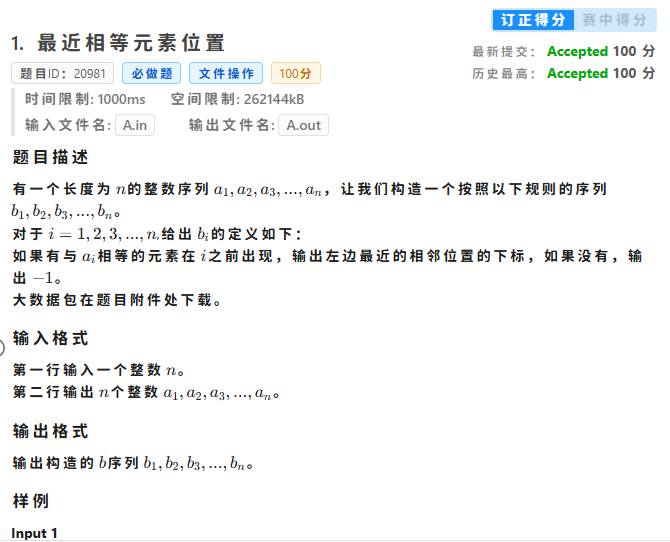
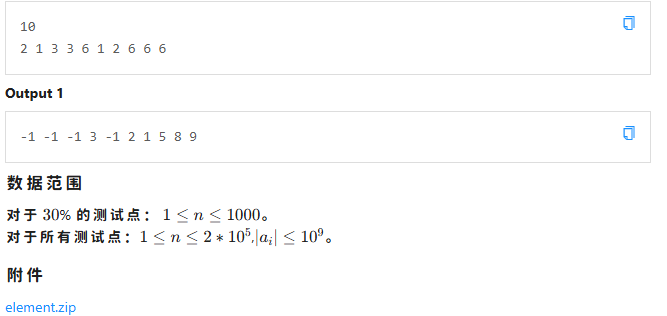
解题思路

非常简单，用一个map统计一下前面的数字下标

枚举每一个数字，看看他前面有没有相同元素，有则输出下标，否则-1

输出完就把这个数放进map中

code

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n;
int a[200005];
int b[200005];
map <int, int> mp;
signed main()
{
    freopen("A.in", "r", stdin);
    freopen("A.out", "w", stdout);
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    for (int i = 1; i <= n; i++)
    {
        if (mp[a[i]] == 0)
        {
            cout << "-1\n";
        }
        else
        {
            cout << mp[a[i]] << endl;
        }
        mp[a[i]] = i;
    }
    return 0;
}

T2

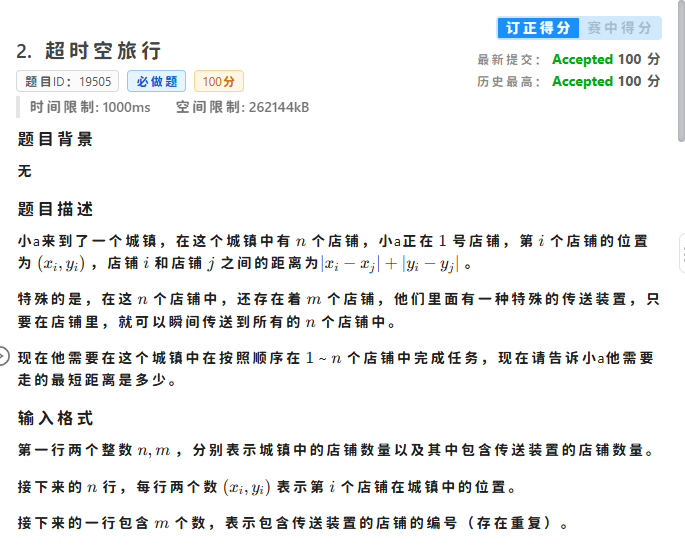
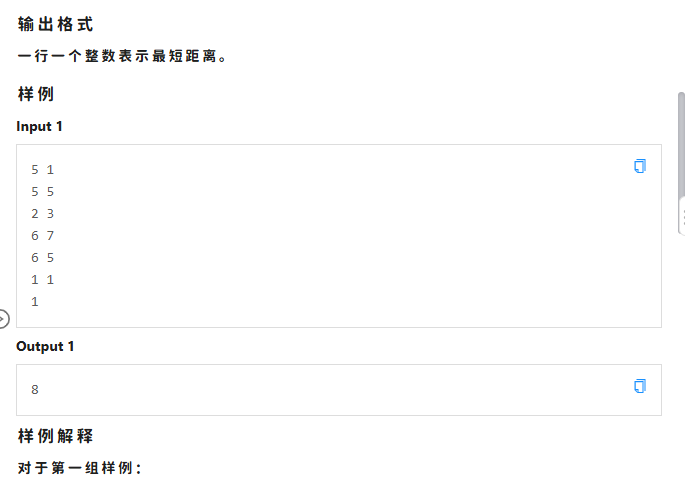
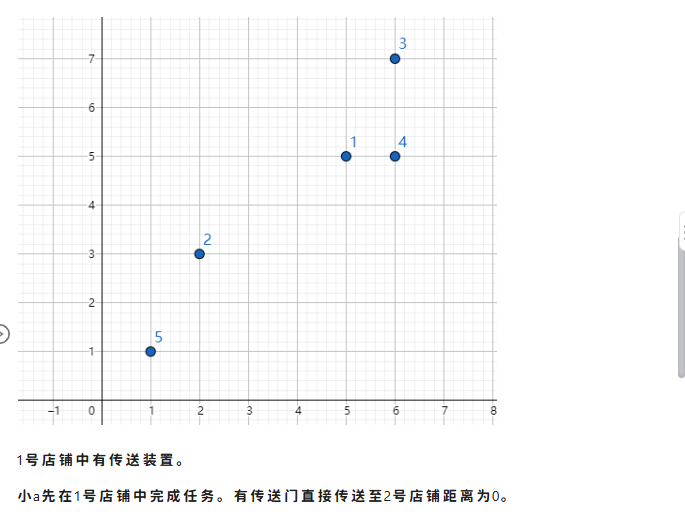
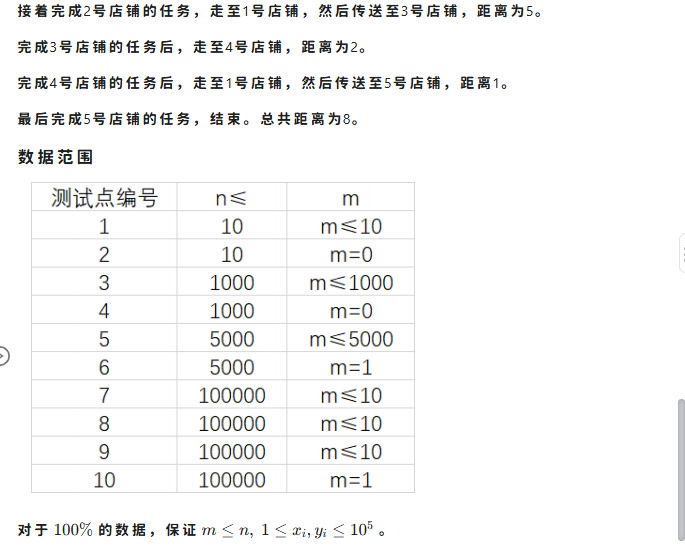
解题思路

枚举2到 \(n\) （因为起点就是第一个店铺）的店铺，计算出走路的时间和最快传送时间（走到最近的可传送店铺的时间），取最小值，把这个加入答案

最后输出答案即可

code

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n, m;
int x[100005], y[100005];
int z[100005];
signed main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> x[i] >> y[i];
    for (int i = 1; i <= m; i++)
        cin >> z[i];
    int ans = 0;
    int nx = x[1];
    int ny = y[1];
    for (int i = 2; i <= n; i++)
    {
        int sum = 1e9;
        for (int j = 1; j <= m; j++)
        {
            int dx = abs(nx - x[z[j]]);
            int dy = abs(ny - y[z[j]]);
            int d = dx + dy;
            sum = min(sum, d);
            // cout << "sum:" << sum << endl;
        }
        sum = min(sum, abs(nx - x[i]) + abs(ny - y[i]));
        ans += sum;
        nx = x[i];
        ny = y[i];
        // cout << i << " " << sum  << " " << nx << " " << ny << endl;
    }
    cout << ans;
    return 0;
}

T3

解题思路

这道题目我有数学题解，详细见此处

\(n= a^2 - b^2\)

我们可以发现，\(n\) 等于两个完全平方数的差

那么我们就可以把一些完全平方数列出来找规律

\(0,1,4,9,16,25,36,49,64……\)

我们从加法规律入手：

\(+1,+3,+5,+7,+9,+11,+13,+15……\)

这些加数是一个以1为首项，公差为2的等差数列

所以，这个等差数列的任何一个字串和就是一个好数字

我们考虑字串和的规律：

• 字串长度为奇数，则和为奇数
• 假如字串长度为1，那么任何奇数都是好数字
• 结论1，所有正奇数都是好数字
• 如果字串长度为偶数，那么和就是4的倍数
• 结论2，4的倍数是好数字

所以，我们只需要计算 \([l,r]\) 区间内奇数的和以及4的倍数的和即可

可以用等差数列求和公式 \((首项+末项)\times 项数 \div 2\) 来计算

code

#include <bits/stdc++.h>
#define int long long
using namespace std;
inline int add4(int l, int r) {
	if (l > r) return 0;
	int first = ((l + 3) / 4) * 4;
	if (first > r) return 0;
	int last = (r / 4) * 4;
	int count = (last - first) / 4 + 1;
	return (first + last) * count / 2;
}
inline int add_ji(int l, int r)
{
	if (l > r) return 0;
	int first, last;
    if (l % 2 == 0) first = l + 1;
    else first = l;
    if (r % 2 == 0) last = r - 1;
    else last = r;
	int count = (last - first) / 2 + 1;
	return (first + last) * count / 2;
}
inline void solve()
{
    int l, r;
    cin >> l >> r;
    cout << add4(l, r) + add_ji(l, r) << endl;
}
signed main()
{
    freopen("count.in", "r", stdin);
    freopen("count.out", "w", stdout);
    int _;
    cin >> _;
    while (_--)
    {
        solve();
    }
    return 0;
}

T4

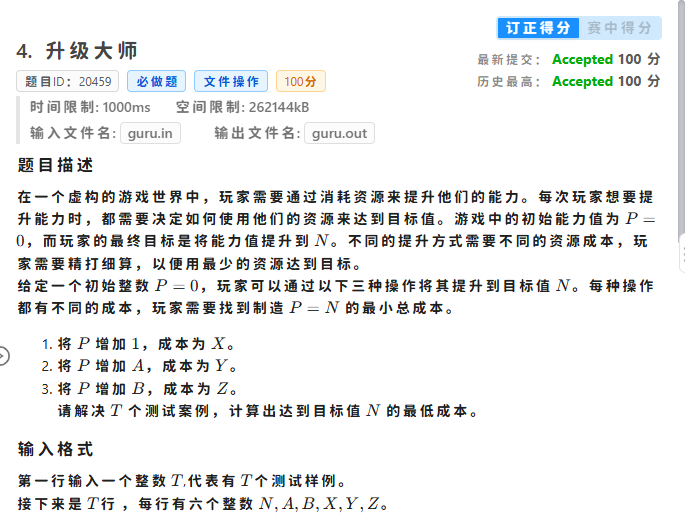
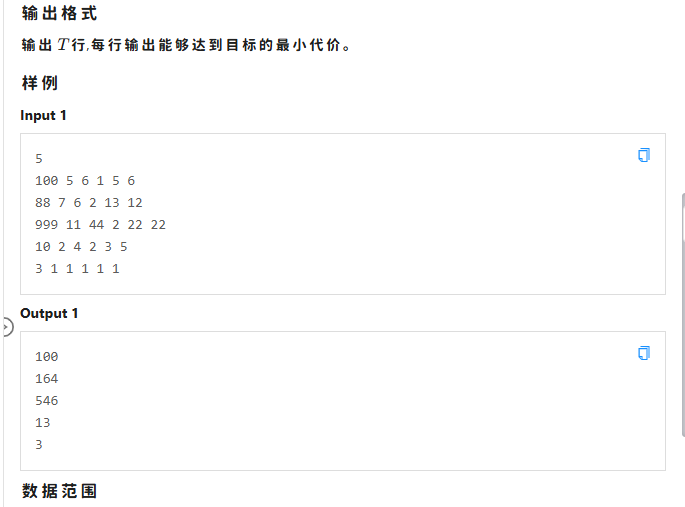
解题思路

先看看那个方案最优（即升1级需要的代价最小）

并且判断，法2和法3那个更优就排在前面（方便后续计算）

• 如果是1个1个的最优，那么输出 \(x\times n\)
• 如果是法2最优，法1其次，那么就一直用法2，最后如果升级不了（即会超过 \(n\)），就用法1填补
• 如果法2最优，法3其次，那么就枚举法2、3的组合，最后升级不了用法1填补，统计处最小值输出

code

#include <bits/stdc++.h>
#define int long long
using namespace std;
inline void solve()
{
    int n, a, b, x, y, z;
    cin >> n >> a >> b >> x >> y >> z;
    if (a * z < b * y)
    {
        swap(a, b);
        swap(y, z);
    }
    int ans = 0;
    if (a * x <= y && b * x <= z)
    {
        ans = n * x;
    }
    else if (a * x > y && b * x <= z)
    {
        ans = n / a * y + (n % a) * x;
    }
    else
    {
        ans = 1e18;
        if (n / a < a)
        {
            for (int i = 0; i * a <= n; ++i)
            {
                int rest = n - i * a;
                int cost = i * y + (rest / b) * z + (rest % b) * x;
                ans = min(ans, cost);
            }
        }
        else
        {
            for (int i = 0; i * b <= n && i < a; ++i)
            {
                int rest = n - i * b;
                int cost = i * z + (rest / a) * y + (rest % a) * x;
                ans = min(ans, cost);
            }
        }
    }
    cout << ans << "\n";
}
signed main()
{
    freopen("guru.in", "r", stdin);
    freopen("guru.out", "w", stdout);
    int _;
    cin >> _;
    while (_--)
    {
        solve();
    }
    return 0;
}

总结

250分还行，T1丢分太可惜

总分：250分

排名：14

AC：2

强省一二等奖

弱省一等奖