10.19日模考总结
本周进行了标准OI普及组模考测试
得分情况
| 题目名称 | 做法 | 预计得分 | 实际得分 |
|---|---|---|---|
| 火车线路 | 模拟 | 100 | 100 |
| 奶牛卧室 | 同余定理 | 100 | 70 |
| 小信的同调序列 | 动态规划 | 10 | 30 |
| 新小信走迷宫 | 贪心、动态规划 | 20 | 40 |
做题流程
首先点开第一题,题目的变量名称真的是一点都不符合逻辑!
不过这题还是较为简单,按照题意模拟一下
用一个数组统计一下火车每一站的载人数,看一下是否超载即可
接着是第二题,乍一看题意倒挺简单,可是想了半天都不知道什么个做法,就先跳过了
随后我看到第三题,考试的时候我估摸,这题是区间 DP,但是我不会写
所以我就暴力出奇迹,枚举每一个区间,看看最大公因数是多少
第四题,非常像搜索,但是这数据范围甚至连地图都存不下
所以我就把数组能开多大开多大,先计算每个位置的成本,用动态规划解决了
最后回到第二题,我列了好久的数学公式,想起了同余定理,于是我就用同余定理来解题了
赛后心得
第一题AC
第二题TLE70分,我觉得没有AC有点可惜,我的思路就是正解,却忘了数组优化和数据范围
第三题30,第四题40,挺高兴的,暴力出奇迹!
题目讲解
T1



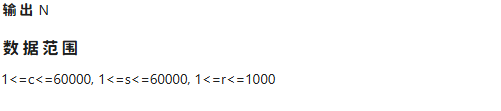
解题思路
维护一个数组来统计每一站火车上的人数
对于每一个请求,先判断其是否可以满足,如果可以,输出 T 并把这个请求的人数加到对应的位置
如果不行,则输出 N
code
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n, m, k;
int l[100005], r[100005], x[100005];
int sum[60005];
signed main()
{
cin >> n >> m >> k;
for (int i = 1; i <= k; i++)
{
cin >> l[i] >> r[i] >> x[i];
}
for (int i = 1; i <= k; i++)
{
bool flag = false;
for (int j = l[i]; j < r[i]; j++)
{
if (sum[j] + x[i] > m)
{
flag = true;
cout << "N\n";
break;
}
}
if (!flag)
{
for (int j = l[i]; j < r[i]; j++)
{
sum[j] += x[i];
}
cout << "T\n";
}
}
return 0;
}
T2

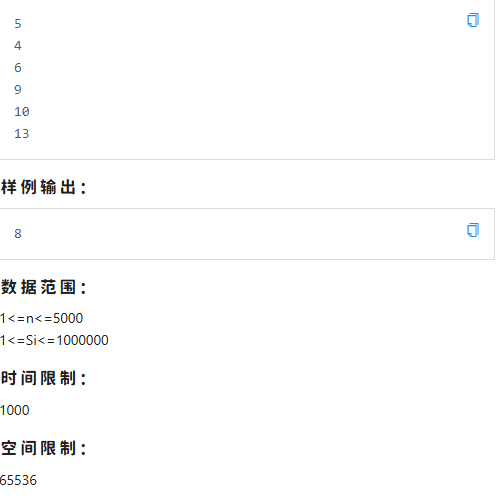
解题思路
我们考虑到,每头牛的床号是 \(a\) \(mod\) \(n\)
那么,“两只牛不能睡在同一个床上” 用数学表达就是 \(a \equiv b (mod\) \(n)\) 不能成立
而且,根据同余定理,如果 \(a \equiv b (mod\) \(n)\) ,则 \((a-b)\) \(mod\) \(n\) \(=\) \(0\)
所以,我们枚举每两个不同奶牛,把他们的差标记一下
\(n\) 头奶牛肯定至少要 \(n\) 个床,而题目保证奶牛编号不相同,所以至多要的床数量是 \(a\) 中的最大值
我们就枚举这中间的值,如果 \(i\) 没有被记录过,那么就输出这个
code
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n;
int a[5005];
bool mp[1000005];
int sum;
signed main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
sum = max(sum, a[i]);
}
for (int i = 1; i < n; i++)
{
for (int j = i + 1; j <= n; j++)
{
int sum = abs(a[i] - a[j]);
mp[sum] = true;
}
}
for (int i = n; i <= sum; i++)
{
if (mp[i] == false)
{
cout << i << endl;
return 0;
}
}
return 0;
}
T3

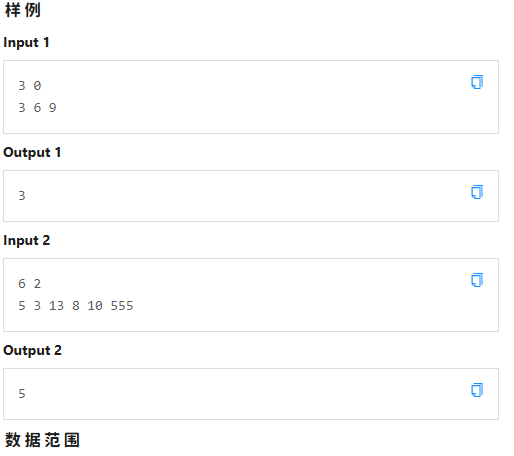
解题思路
我们可以维护一个DP数组,\(dp_{i}\) 指遍历到的元素下标(也就是当前区间结尾)
我们再开启一个维度,0表示这个元素不 \(+k\) ,1表示 \(+k\), 2表示中断(即以后都不 \(+k\))
这样一来,题目就简单的许多
对于1,我们进行初始化
接着,我们枚举2至 \(n\) :
- \(dp_{i,0}\) :一种情况,从上一个状态0出发
- \(dp_{i,1}\) :情况1,从上一个状态0出发;情况2,从上一个状态1出发
- \(dp_{i,2}\) :情况1,从上一个状态1出发;情况2,从上一个状态2出发
最后输出 \(max(dp_{n,0},dp_{n,1},dp_{n,2})\) 即可
code
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n, k;
int a[300005];
int dp[300005][3];
signed main()
{
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
dp[1][0] = a[1];
dp[1][1] = a[1] + k;
dp[1][2] = a[1];
for (int i = 2; i <= n; i++)
{
dp[i][0] = __gcd(dp[i - 1][0], a[i]);
dp[i][1] = max(__gcd(dp[i - 1][1], a[i] + k), __gcd(dp[i - 1][0], a[i] + k));
dp[i][2] = max(__gcd(dp[i - 1][2], a[i]), __gcd(dp[i - 1][1], a[i]));
}
cout << max(max(dp[n][0], dp[n][1]), dp[n][2]);
return 0;
}
T4



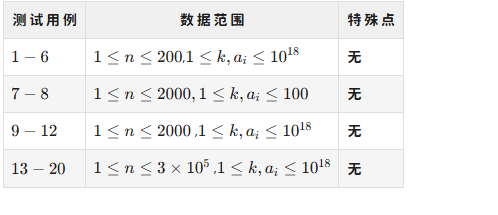
解题思路
第一反应肯定是棋盘DP模板,但是数据范围太大,空间与时间都不够
所以我们可以先进行一个贪心,既然成本最小,说明格子中的成本也得最小,也就是说,\(gcd(i,a),gcd(j,b)\) 越小越好
所以尽量把这两个值变小(变成1是最优的)
而变成1,一般常见有两种情况:两数中有1或者有质数
考虑1的情况,那么就是:
- 出发后尽量多贴着第一行走
- 出发后尽量多贴着第一列走
再考虑质数的情况,我们可以从大到小枚举行数和列数,找到最大行列 \(x,y\)
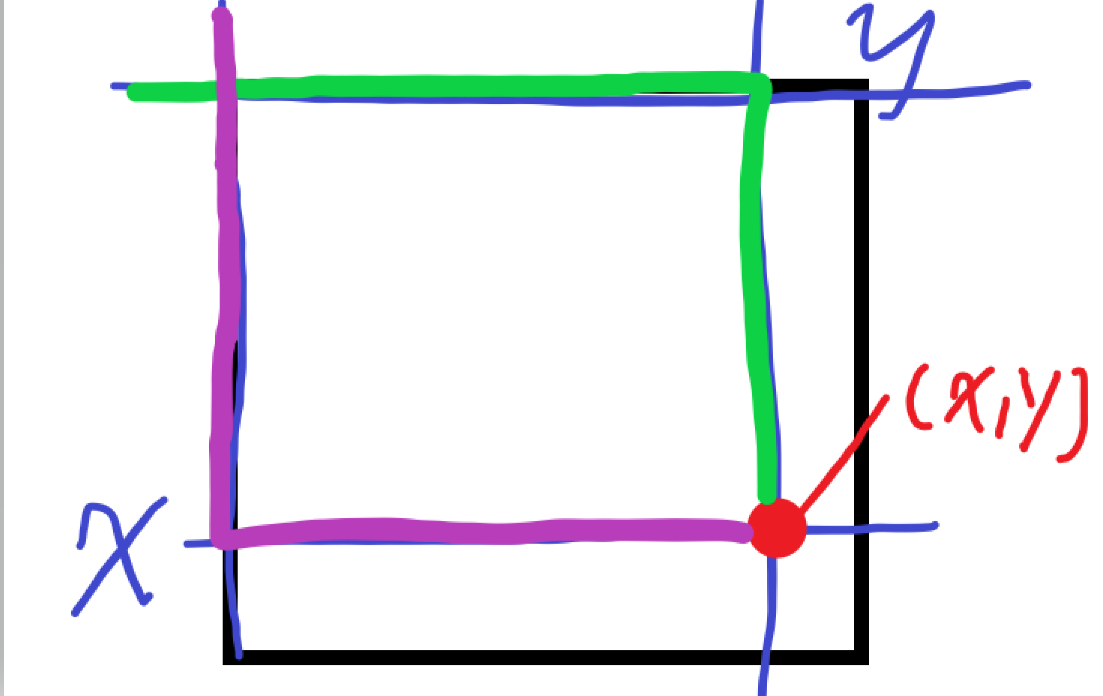
经过一些计算(这里不展示了),我们得知,紫色路线与绿色路线的成本相同
所以,我们先通过紫色或绿色路线来到点 \((x,y)\),这是最优选择
而我们发现,右下角还剩一个小框框没有计算,这个小框框的面积肯定不大,这个时候我们再用棋盘DP模板计算小框框的最小成本,把颜色路线与小框框成本加起来就是答案
可能有点抽象,请细细品读
code
#include <bits/stdc++.h>
using namespace std;
int n;
int a, b;
int dp[10005][10005];
int main()
{
cin >> n >> a >> b;
int x, y, ans = 0;
for (x = n; x >= 1; x--)
{
if (__gcd(x, a) == 1)
break;
}
for (y = n; y >= 1; y--)
{
if (__gcd(y, b) == 1)
break;
}
for (int i = 1; i <= x; i++)
{
ans += __gcd(i, a);
}
for (int i = 1; i <= y; i++)
{
ans += __gcd(i, b);
}
memset(dp, 0x3f, sizeof(dp));
dp[1][1] = ans + (x - 1) + (y - 1);
for (int i = x; i <= n; i++)
{
for (int j = y; j <= n; j++)
{
if (i == x && j == y)
continue;
dp[i - x + 1][j - y + 1] = min(dp[i - x][j - y + 1], dp[i - x + 1][j - y]) + __gcd(i, a) + __gcd(j, b);
}
}
cout << dp[n - x + 1][n - y + 1];
return 0;
}
总结
总分240分还不错,应该可以拿省一,T2丢分太可惜了
总分:240
排名:2
AC:1
强省一二等奖,弱省一等奖







 浙公网安备 33010602011771号
浙公网安备 33010602011771号